Stevinsches Gedankenexperiment

Das Stevinsche Gedankenexperiment ist nach seinem Urheber, dem flämischen Physiker Simon Stevin (1548–1620) benannt, der damit das Kräftegleichgewicht auf schiefen Ebenen erklärte und das Kräfteparallelogramm (Zerlegung von Kräften als Vektoren) einführte. Es hat historische Bedeutung, weil es eines der ersten bekannten Gedankenexperimente darstellt, mit dem in einer Naturwissenschaft ein Erkenntnisgewinn erzielt werden konnte.[1][2]

Titelseite Hypomnemata mathematica mit der Vignette des Gedankenexperiments

Hauptteil

Stevin behandelt Kräfte auf der schiefen Ebene in seinem Buch über Statik (De Beghinselen der Weegconst 1586, das niederländische Weeghconst, übersetzt Kunst des Wiegens) in Proposition XIX. Er hatte zuvor das Hebelgesetz behandelt nach dem Vorbild von Archimedes, dieser behandelte aber nicht schräg angreifende Kräfte wie auf der schiefen Ebene, und die Behandlung nach Jordanus Nemorarius benutzte die Methode virtueller Verschiebungen bzw. virtueller Arbeit, die Stevin nicht verwenden wollte und kritisierte, da es bei Jordanus keiner statischen Überlegung entsprach, sondern Körpern in Bewegung. Stevin behandelt das Thema wie Archimedes in strenger mathematischer Logik. Sein Fachausdruck für die Kraftkomponenten (niederländisch stalwicht) ist nach Eduard Jan Dijksterhuis[3] schwer zu übersetzen, in etwa scheinbares Gewicht. Im Fall der geschlossenen Kette von Kugeln (niederländisch Clootcrans, Kugelkranz) entspricht sie der längs der schiefen Ebene wirkenden Kraft. Aus heutiger Sicht ist es die Einführung der Vektorzerlegung der Kraft oder des Parallelogramms der Kräfte.

Stevins Theorien wurden nach seinem Tod auch in der damaligen Wissenschaftssprache Latein in seinen Hypomnemata mathematica (Gesammelte mathematische Werke) veröffentlicht – wodurch sie weitere Verbreitung fanden – und Ernst Mach sieht in der Behandlung dort (und in der der schiefen Ebene bei Galileo Galilei) den Ursprung des Prinzips der virtuellen Verschiebungen in der Statik,[4] ausgebaut von Johann I Bernoulli (Brief an Pierre de Varignon 1717). Frühe Formen der linearen Zusammensetzung von Kräften oder allgemein physikalischen Größen der Bewegung (vor der Entwicklung des Kraftbegriffs im heutigen Sinn) gehen bis auf Pseudo-Aristoteles (Questiones Mechanicae) zurück. Die spätere Entwicklung zu einer Interpretation im heutigen Sinn geschah besonders im 17. Jahrhundert in Frankreich und England, ist verwickelt und führte schließlich zur Formulierung als Korollar 1 zu den drei als Axiom formulierten Bewegungsgesetzen in der Principia von Isaac Newton.[5] Varignon fand später unabhängig das Gesetz des Kräfteparallelogramms (1687 und später).

Der Beweis von Stevin wurde von späteren bedeutenden Mathematikern, Physikern und Wissenschaftshistorikern wie Ernst Mach und Eduard Jan Dijksterhuis sehr bewundert, und Stevin selbst war so stolz darauf, dass er die Grafik dazu (mit der Legende WONDER EN IS GHEEN WONDER, übersetzt: „Das Wunder ist, dass es kein Wunder gibt“) in den meisten seiner Werke als Vignette verwendete und auf seinem Grabstein.[6] Der Nobelpreisträger Richard Feynman kommentiert in seinen Vorlesungen über Physik: If you are getting a diagram like this on your gravestone, you are doing fine (Wenn Sie ein Diagramm wie dieses auf Ihrem Grabstein haben, haben Sie alles richtig gemacht).[7]

Erläuterung
Schema des Beweises.

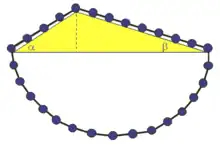
Auf einem Dreieck mit zwei schiefen Ebenen verschiedener Neigung liegt eine geschlossene Kugelkette. Die Erfahrung lehrt, dass die Kette nicht von selbst rotiert, wenn sie nicht angestoßen wird. Andernfalls wäre die Vorrichtung ein Perpetuum mobile, das Stevin unmöglich erschien und nach heutiger Auffassung aufgrund der Energieerhaltung ausgeschlossen ist. Da der untere Teil der Kette symmetrisch unter dem Dreieck hängt, kann dieser entfernt werden, ohne das Gleichgewicht der verbleibenden Kette zu stören. In dem Beispiel der Abbildung sind vier Kugeln auf der linken schiefen Ebene und acht in der rechten schiefen Ebene. Die Kräfte längs der schiefen Ebenen sind jeweils (mit der Masse einer Kugel und der Gravitationsbeschleunigung)

und im Scheitelpunkt im Gleichgewicht. Also mit den Bezeichnungen in der Abbildung

Daraus folgt:

Das heißt die Kräfte längs der schiefen Ebenen verhalten sich wie die Sinuse der Winkel gegen die Horizontale, also gleich den Längen (Projektion auf die Horizontale) der beiden schiefen Ebenen, die gleiche Höhe haben.

Literatur
  • Erik Jan Dijksterhuis: Simon Stevin, Nijhuis 1970
  • Henning Genz: Gedankenexperimente, Physik in unserer Zeit, Band 27, 1996, Nr. 2, S. 79–80
  • Henning Genz: Gedankenexperimente, Wiley-VCH 1999
  • Bergmann-Schaefer: Lehrbuch der Experimentalphysik - Band I - Mechanik, Akustik, Wärme, Walter de Gruyter, Berlin, 9. Auflage 1974, Kapitel II, 61f
Statue von Simon Stevin von Louis-Eugène Simonis (1811–1893) auf dem Place Simon Stevin in Brügge

Einzelnachweise
  1. Henning Genz, Gedankenexperimente, Wiley-VCH 1999, S. 55
  2. Julian Nida-Rümelin (Herausgeber): Rationalität, Realismus, Revision, Gedankenexperimente in Erkenntnistheorie und Physik, Seite 461, Gesellschaft für Analytische Philosophie, Walter de Gruyter, 2000, ISBN 978-3-11-016393-3
  3. Dijksterhuis, Simon Stevin, Nijhoff 1970, S. 52
  4. Mach, Die Mechanik in ihrer Entwicklung, Brockhaus 1883, S. 47
  5. David Marshall Miller, The parallelogram-rule from Pseudo-Aristoteles to Newton, Archive Hist. Exact Sci., Band 71, 2016, S. 157–191.
  6. Dijksterhuis, Stevin, 1970, S. 54
  7. Richard Feynman: The Feynman Lectures on Physics - Volume 1,, Addison-Wesley Publishing Company, Reading, Massachusetts, 1963, Kapitel 4
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.