Spirale

Archimedische Spirale

Man kann Spiralen mathematisch am besten als Koordinatengleichungen im ebenen Polarkoordinatensystem beschreiben, wobei ${\displaystyle r}$ als Funktion ${\displaystyle r(\varphi )}$ von ${\displaystyle \varphi }$ dargestellt wird; ${\displaystyle \varphi }$ läuft im Allgemeinen bis unendlich anstatt nur bis 2π. Auch negative Winkel sind möglich.

Polardarstellung einer Spirale:

• ${\displaystyle r=r(\varphi )}$

In ${\displaystyle x}$-${\displaystyle y}$-Koordinaten werden dadurch Punkte mit der Parameterdarstellung

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi }$

beschrieben.

Ersetzt man in der Polardarstellung ${\displaystyle \varphi }$ durch ${\displaystyle \varphi -\varphi _{0}}$, so wird die Spirale um den Winkel ${\displaystyle \varphi _{0}}$ gedreht. (Eventuell muss der Definitionsbereich angepasst werden.)

• Archimedische Spirale: ${\displaystyle \ r=a\varphi }$
• Hyperbolische Spirale: ${\displaystyle \ r={\tfrac {a}{\varphi }}}$
• Fermatsche Spirale: ${\displaystyle \ r=a{\sqrt {\varphi }}}$
• Lituus-Spirale: ${\displaystyle \ r={\tfrac {a}{\sqrt {\varphi }}}}$
• Logarithmische Spirale: ${\displaystyle \ r=ae^{k\varphi }}$

Hyperbolische Spirale als Zentralprojektion einer Schraubenlinie

Die archimedische Spirale entsteht z. B. beim Aufwickeln eines gleichmäßig dicken Teppichs. Sie wird in der ${\displaystyle r}$-${\displaystyle \varphi }$-Ebene durch eine Gerade beschrieben.

Die hyperbolische Spirale wird in der ${\displaystyle r}$-${\displaystyle \varphi }$-Ebene durch eine Hyperbel beschrieben. Sie entsteht bei der Zentralprojektion einer Schraubenlinie auf eine zur Schraubachse senkrechte Ebene (siehe Bild). Man sieht sie z. B. beim senkrechten Blick durch eine Wendeltreppe (siehe hierzu Schraublinie (Darstellende Geometrie)). Sie ist auch das Bild einer archimedischen Spirale bei einer Kreisspiegelung (Inversion).

Die Fermatsche Spirale heißt auch parabolische Spirale, da ihre Polargleichung eine Parabel beschreibt.

Die Lituus-Spirale ist das Bild einer fermatschen Spirale bei einer Kreisspiegelung.

Die logarithmische Spirale entsteht z. B. beim Wachstum von Schneckenhäusern. Ihr Name rührt von der Auflösung ihrer Polargleichung nach ${\displaystyle \varphi }$ her: ${\displaystyle \varphi ={\tfrac {1}{k}}\cdot \ln {\tfrac {r}{a}}}$.

• 
  Hyperbolische Spirale:
  ${\displaystyle r={\frac {a}{\varphi }}}$
• 
  Fermatsche Spirale:
  ${\displaystyle r=a{\sqrt {\varphi }}}$
• 
  Lituus-Spirale:
  ${\displaystyle r={\frac {a}{\sqrt {\varphi }}}}$
• 
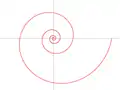  Logarithmische Spirale:
  ${\displaystyle r=ae^{k\varphi }}$

Neben diesen Spiralen gibt es noch solche, die nicht in dieses Konzept passen:

• Spirale des Theodorus. Sie ist keine glatte Kurve, sondern ein Polygon mit den Seitenlängen 1.
• Klothoide (Cornu-Spirale). Sie besitzt zwei asymptotische Punkte.

• 
  Spirale des Theodorus
• 
  Cornu-Spirale

Polarkoordinaten: Definition von Sektor (hellblau) und polarer Steigungswinkel (${\displaystyle \alpha }$)

Polarer Steigungswinkel

Der Winkel ${\displaystyle \alpha }$, unter dem die Spiraltangente den zugehörigen Polarkreis schneidet, heißt polarer Steigungswinkel und ${\displaystyle \tan \alpha }$ die polare Steigung. Aus der Formel für den Tangentenvektor ergibt sich

${\displaystyle \tan \alpha ={\frac {r'}{r}}\ .}$

Für eine Spirale mit der Gleichung ${\displaystyle \;r=a\varphi ^{n}\;}$ ist die polare Steigung

• ${\displaystyle \tan \alpha ={\frac {n}{\varphi }}\ .}$

Für die archimedische Spirale ist ${\displaystyle n=1}$ und damit ${\displaystyle \;\tan \alpha ={\tfrac {1}{\varphi }}\ .}$

Für die logarithmische Spirale ist ${\displaystyle \ \tan \alpha =k\ }$ konstant.

Krümmung

Die Krümmung ${\displaystyle \kappa }$ einer Kurve in Polardarstellung ist

${\displaystyle \kappa ={\frac {r^{2}+2(r')^{2}-r\;r''}{(r^{2}+(r')^{2})^{3/2}}}\ .}$

Für eine Spirale mit der Gleichung ${\displaystyle r=a\varphi ^{n}}$ ergibt sich

• ${\displaystyle \kappa =\dotsb ={\frac {1}{a\varphi ^{n-1}}}{\frac {\varphi ^{2}+n^{2}+n}{(\varphi ^{2}+n^{2})^{3/2}}}\ .}$

Z. B. ist für ${\displaystyle n=1}$ (archimedische Spirale) ${\displaystyle \kappa ={\tfrac {\varphi ^{2}+2}{a(\varphi ^{2}+1)^{3/2}}}}$. Die Spirale hat also keinen Wendepunkt.

Die Krümmung einer logarithmischen Spirale ${\displaystyle \;r=ae^{k\varphi }\;}$ ist ${\displaystyle \;\kappa ={\tfrac {1}{r{\sqrt {1+k^{2}}}}}\;.}$

Sektorfläche

Die Fläche eines Kurvensektors einer Kurve in Polardarstellung ist

${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\;d\varphi \ .}$

Für eine Spirale mit der Gleichung ${\displaystyle r=a\varphi ^{n}\;}$ ergibt sich

• ${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}a^{2}\varphi ^{2n}\;d\varphi ={\frac {a^{2}}{2(2n+1)}}{\big (}\varphi _{2}^{2n+1}-\varphi _{1}^{2n+1}{\big )}\ ,\quad {\text{falls}}\quad n\neq -{\frac {1}{2}},}$
• ${\displaystyle A={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{\varphi }}\;d\varphi ={\frac {a^{2}}{2}}(\ln \varphi _{2}-\ln \varphi _{1})\ ,\quad {\text{falls}}\quad n=-{\frac {1}{2}}\ .}$

Die Sektorfläche einer logarithmischen Spirale ${\displaystyle \;r=ae^{k\varphi }\;}$ ist ${\displaystyle \ A={\tfrac {r(\varphi _{2})^{2}-r(\varphi _{1})^{2})}{4k}}\ .}$

Bogenlänge

Die Länge eines Bogens einer Kurve in Polardarstellung ist

${\displaystyle L=\int \limits _{\varphi _{1}}^{\varphi _{2}}{\sqrt {\left(r^{\prime }(\varphi )\right)^{2}+r^{2}(\varphi )}}\,\mathrm {d} \varphi \ .}$

Für eine Spirale mit der Gleichung ${\displaystyle r=a\varphi ^{n}\;}$ ergibt sich

• ${\displaystyle L=\int _{\varphi _{1}}^{\varphi _{2}}{\sqrt {{\frac {n^{2}r^{2}}{\varphi ^{2}}}+r^{2}}}\;d\varphi =a\int \limits _{\varphi _{1}}^{\varphi _{2}}\varphi ^{n-1}{\sqrt {n^{2}+\varphi ^{2}}}d\varphi \ .}$

Diese Integrale sind nicht mehr für alle ${\displaystyle n}$ geschlossen lösbar. Im Fall der fermatschen Spirale ergibt sich ein elliptisches Integral.

Die Bogenlänge einer logarithmischen Spirale ${\displaystyle \;r=ae^{k\varphi }\;}$ ist ${\displaystyle \ L={\tfrac {\sqrt {k^{2}+1}}{k}}{\big (}r(\varphi _{2})-r(\varphi _{1}){\big )}\ .}$

Beschränkte Spiralen:
${\displaystyle r=a\arctan(k\varphi )}$ (links),
${\displaystyle r=a(\arctan(k\varphi )+\pi /2)}$ (rechts)

Die Funktion ${\displaystyle r(\varphi )}$ einer Spirale ist üblicherweise eine streng monotone, stetige Funktion und unbeschränkt. In den Standardbeispielen ist ${\displaystyle r(\varphi )}$ eine Potenzfunktion oder eine Exponentialfunktion. Man kann allerdings für ${\displaystyle r(\varphi )}$ auch eine beschränkte streng monotone Funktion wählen und erhält damit dann eine beschränkte Spirale. Eine hierfür geeignete Funktion ist der Arkustangens:

Beispiel 1

Setzt man ${\displaystyle \;r=a\arctan(k\varphi )\;}$ und wählt ${\displaystyle \;k=1/10,\;a=4,\;\varphi \geq 0}$, erhält man eine Spirale, die im Ursprung beginnt (wie die archimedische Spirale) und sich dem Kreis mit Radius ${\displaystyle \;r=2\pi \;}$ annähert (im Bild links).

Beispiel 2

Setzt man ${\displaystyle \;r=a(\arctan(k\varphi )+\pi /2)\;}$ und wählt ${\displaystyle \;k=1/5,\;a=2,\;-\infty <\varphi <\infty }$, erhält man eine Spirale, die sich dem Ursprung nähert (wie die hyperbolische Spirale) und sich dem Kreis mit Radius ${\displaystyle \;r=2\pi \;}$ annähert (im Bild rechts).

Ist in der ${\displaystyle x}$-${\displaystyle y}$-Ebene durch die Parameterdarstellung

${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi }$

eine ebene Spirale gegeben, so kann man eine dritte Koordinate ${\displaystyle z(\varphi )}$ so anfügen, dass die dadurch entstehende räumliche Kurve auf dem senkrechten Kreiskegel mit der Gleichung ${\displaystyle \;m^{2}(x^{2}+y^{2})=(z-z_{0})^{2}\ ,\ c>0\;}$ liegt:

• ${\displaystyle x=r(\varphi )\cos \varphi \ ,\qquad y=r(\varphi )\sin \varphi \ ,\qquad \color {red}{z=z_{0}+mr(\varphi )}\ .}$

Spiralen dieser Art nennt man konische Spiralen.[1] Sie waren auch schon Pappos bekannt.

Beispiel

Geht man von einer archimedischen Spirale ${\displaystyle \;r(\varphi )=a\varphi \;}$ aus, erhält man die konische Spirale (siehe Bild)

${\displaystyle x=a\varphi \cos \varphi \ ,\qquad y=a\varphi \sin \varphi \ ,\qquad z=z_{0}+ma\varphi \ ,\quad \varphi \geq 0\ .}$

In diesem Fall kann man die konische Spirale auch als Schnittkurve eines Kegels und einer Wendelfläche auffassen.

Kugelspirale mit ${\displaystyle c=8}$

Stellt man eine Kugel mit Radius ${\displaystyle r}$ in Kugelkoordinaten dar:

${\displaystyle {\begin{aligned}x&=r\cdot \sin \theta \cdot \cos \varphi \\y&=r\cdot \sin \theta \cdot \sin \varphi \\z&=r\cdot \cos \theta \end{aligned}}}$

und gibt eine lineare Abhängigkeit der Winkel ${\displaystyle \;\varphi =c\theta ,\;c>2\;}$ vor, so erhält man eine Kugelspirale[2] mit der Parameterdarstellung

• ${\displaystyle {\begin{aligned}x&=r\cdot \sin \theta \cdot \cos {\color {red}c\theta }\\y&=r\cdot \sin \theta \cdot \sin {\color {red}c\theta }\\z&=r\cdot \cos \theta \qquad \qquad 0\leq \theta \leq \pi \ .\end{aligned}}}$

Auch Kugelspiralen wurden schon von Pappus untersucht. Sie sind spezielle Clelia-Kurven.

Lässt man ${\displaystyle c=1}$ also ${\displaystyle \;\varphi =\theta \;}$ zu, erhält man eine vivianische Kurve.

Man beachte: Eine Loxodrome ist keine Kugelspirale in dem hier erklärten Sinne.

• 
  Kugelspirale
• 
  Loxodrome

Newgrange – Stein am Eingang.
In der linken Bildhälfte deutet sich bereits eine Triplespirale (Triskele) an.

Mit Spiralen dekorierte Vase aus der ägyptischen Naqada-II-Zeit

Spiralen tauchen bereits in vor- und frühgeschichtlicher Zeit als häufiges Ornamentmotiv auf Stein und Keramik auf. Beispiele finden sich in der Bandkeramik der Jungsteinzeit, aber auch in den frühen Hochkulturen Ägyptens, Kretas und Chinas. In Europa sind Spiralmotive von den Megalithkulturen über die Bronzezeit bis zur frühen Eisenzeit sowie bei den Kelten und Germanen verbreitet und erscheinen auch auf iberischer Keramik.

Spiralen vermitteln eine Vorstellung von Unendlichkeit, sie können aber auch unheilabwehrend (apotropäisch) gemeint sein oder sogar als Stammeszeichen fungieren.[3]

Tripelspirale als vorzeitliches Motiv (Triskele) oder Celtic Triskele

In der Kirche von Vallstena wurde ein gotländischer Bildstein gefunden, dessen Mittelteil mit einem vierfachen Spiralornament verziert ist. Das Zeichen, das als Tripelspirale wesentlich älter ist und ansatzweise im Passage tomb von Newgrange in Irland vorkommt, ist auf Gotland als 4-, 6- und 7-fache Kombination anzutreffen. Auch stilisierte Tierköpfe sowie realistischere Bilder von Menschen und Tieren sind bisweilen mit diesem geometrischen Motiv vereint. Es handelt sich bei der Spirale, ebenso wie beim Wirbelrad, vermutlich um ein Sonnensymbol oder die Darstellung einer Göttervielheit. Farbe unterstützte das flache, aber fein gehauene Ornament und hob die Darstellung hervor. Das Spiralmotiv kommt in verschiedener Form und Komposition auf den älteren Steinen, die zwischen 400 und 600 n. Chr. entstanden, vor. Spiralmotive tauchen aber sowohl früher als auch später in verschiedenen Fundzusammenhängen auf. Auf den Britischen Inseln sind sie um Christi Geburt verbreitet, und in der mehrere Jahrhunderte jüngeren spätkeltischen Kunst können sie in frühchristlichen Handschriften studiert werden. Diese Kunst steht den Bildsteinen zeitlich näher; es ist daher vermutet worden, dass ein gewisser Zusammenhang besteht.

In der europäischen Kunst des Mittelalters (Romanik und Gotik) sind Spiralmotive eher selten anzutreffen, obwohl – vor allem im gotischen Maßwerk – geometrische Spiele (ludi geometrici) häufig waren und in der Spätgotik auch zu zentrierten und gezogenen Dreipassformen führten, die Erinnerungen an ältere Spiralmotive wachrufen. Dagegen nehmen Labyrinthe, Flechtbänder, Rankenwerk und andere gewundene, aber sehr oft auch – anders als bei den Spiralen – sich überschneidende Dekormotive an Zahl zu. Im Tympanonfeld der Kirche von Bembrive (Provinz Pontevedra, Spanien) sind drei Spiralen zu sehen; die Stirnseite des inneren Portalbogens der Kirche von San Pedro de Gaíllos (Provinz Segovia, Spanien) zeigt – neben Rosetten und Wirbeln – auch kleine Spiralen. An mittelalterlichen Tür- und Truhenbeschlägen findet man sie häufiger – dort entwickeln sie sich jedoch aus geraden Bändern.

• 
  Kapitell in Swartnoz, Armenien (7. Jh.)
• 
  Portal der Kirche von San Pedro de Gaíllos, Detail
• 
  Tympanonfeld der Kirche von Bembrive
• 
  Kapitell der Kirche von Franchesse
• 
  Spiralförmige Beschläge an der Tür der Kirche von Navata
• 
  Spiralförmige Beschläge an der Tür der Kirche von Prats-de-Mollo-la-Preste

In der Renaissance fand die Spirale Einzug in die Arabeske und Groteske, in der Architektur ist sie in der Volute sowie im Rollwerk und im Manierismus in der charakteristischen figura serpentinata anzutreffen.[3] Späte Höhepunkte erleben Spiralen in den Voluten der Barockzeit und im Jugendstil (z. B. bei Gustav Klimt).

Friedensreich Hundertwasser verwendete in seinem eigenen Kunststil die Spirale als Symbol von Geburt und Tod gleichermaßen und liebte sie, da sie der geraden Linie entgegenwirkte.