Satz von Wagner und Fáry

Der Satz von Wagner und Fáry, manchmal auch als Satz von Wagner oder Satz von Fáry bezeichnet, ist ein Lehrsatz aus dem mathematischen Teilgebiet der Topologischen Graphentheorie, welcher zuerst im Jahre 1936 von dem Mathematiker Klaus Wagner gefunden und dann im Jahre 1948 von dem Mathematiker István Fáry erneut gefunden wurde. Der Satz behandelt eine wichtige Eigenschaft plättbarer Graphen, die nicht zuletzt im Zusammenhang mit dem Vierfarbensatz und verwandten mathematischen Lehrsätzen von Bedeutung ist.

Formulierung des Satzes
Nach einem geeigneten Homöomorphismus sind auch B und D durch eine Strecke verbunden.

Erste Version

Die erste Version des Satzes lautet wie folgt:[1]

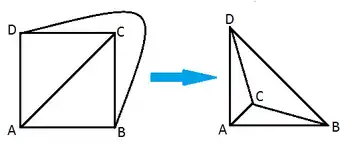
Ist ein endlicher schlichter Graph plättbar, so existiert sogar ein isomorpher ebener Graph dergestalt, dass die zu den Kanten gehörigen Jordankurven sämtlich abgeschlossene Strecken sind, die einander nie in einem inneren Punkt kreuzen, also paarweise stets höchstens einen der Knoten gemeinsam haben.

Zweite Version

Ein ebener Graphen der in der ersten Version genannten Art wird auch als Streckengraph oder als geradlinige Darstellung (des Graphen ) bezeichnet. Unter Verwendung dieser Begriffe lässt sich der Satz auch folgendermaßen formulieren:[2][3]

Jeder ebene Graph kann durch einen Homöomorphismus der euklidischen Ebene auf sich in einen Streckengraphen überführt werden.

Anmerkungen
  • Die Bedeutung des Satzes von Wagner und Fáry (in der zweiten Version) für den Vierfarbensatz geht aus einer Anmerkung hervor, die der Mathematiker Rudolf Fritsch in seiner Monographie Der Vierfarbensatz dazu macht. Fritsch schreibt, dass der Satz die endgültige Befreiung aus dem Gruselkabinett beliebiger Jordankurven bringt und den Vierfarbensatz aus den Klauen der allgemeinen Topologie löst.[4]
  • Die Vermutung, dass die Aussage des Satzes von Wagner und Fáry gelte, wurde István Fáry zufolge schon früher von dem ungarischen Mathematiker Tibor Szele geäußert.[4]

Siehe auch

Literatur
  • István Fáry: On straight line representation of planar graphs. In: Acta Univ. Szeged. Sect. Sci. Math. Band 11, 1948, S. 229–233 (MR0026311).
  • Rudolf Fritsch: Der Vierfarbensatz. Geschichte, topologische Grundlagen und Beweisidee. Unter Mitarbeit von Gerda Fritsch. BI Wissenschaftsverlag, Mannheim / Leipzig / Wien / Zürich 1994, ISBN 3-411-15141-2 (MR1270673).
  • Rudolf Halin: Graphentheorie II (= Erträge der Forschung. Band 161). Wissenschaftliche Buchgesellschaft, Darmstadt 1981, ISBN 3-534-08269-9 (MR0668698).
  • Nora Hartsfield, Gerhard Ringel: Pearls in Graph Theory. A Comprehensive Introduction. Academic Press, Boston (u. a.) 1990, ISBN 0-12-328552-6 (MR1069559).
  • Jonathan L. Gross, Thomas W. Tucker: Topological Graph Theory (= Wiley-Interscience Series in Discrete Mathematics and Optimization). John Wiley & Sons, New York 1987, ISBN 0-471-04926-3 (MR0898434).
  • Klaus Wagner: Bemerkungen zum Vierfarbenproblem. In: Jahresbericht der Deutschen Mathematiker-Vereinigung. Band 46, 1936, S. 26–32.
  • Klaus Wagner: Graphentheorie (= BI-Hochschultaschenbücher. 248/248a). Bibliographisches Institut, Mannheim (u. a.) 1970, ISBN 3-411-00248-4 (MR0282850).

Einzelnachweise und Anmerkungen
  1. Nora Hartsfield, Gerhard Ringel: Pearls in Graph Theory. 1990, S. 166–167
  2. Rudolf Fritsch: Der Vierfarbensatz. 1994, S. 106 ff., 113–115
  3. Rudolf Halin: Graphentheorie II. 1981, S. 9 ff., 14–15
  4. Fritsch, op. cit., S. 107
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.