Satz von Menelaos

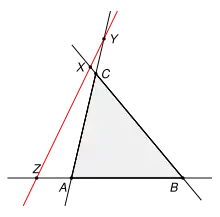
Gegeben seien ein Dreieck ABC und eine Gerade, welche die Dreiecksseiten [BC], [CA] und [AB] beziehungsweise ihre Verlängerungen in den Punkten X, Y und Z schneidet. Dann gilt:

${\displaystyle TV(B,C,X)\cdot TV(C,A,Y)\cdot TV(A,B,Z)=-1}$

Umgekehrt kann man aus der Richtigkeit dieser Beziehung folgern, dass die Punkte X, Y und Z auf einer Geraden liegen.

Hierbei ist ${\displaystyle TV(U,V,W)}$ das Teilverhältnis von ${\displaystyle U,V,W}$, das für drei auf einer Geraden liegende Punkte ${\displaystyle U,V,W}$ mit ${\displaystyle U\neq V}$ definiert wird durch ${\displaystyle W=U+TV(U,V,W)\cdot (V-W)}$. Wenn ${\displaystyle W}$ zwischen ${\displaystyle U}$ und ${\displaystyle V}$ liegt, ist dieses Teilverhältnis gleich ${\displaystyle {\overline {UW}}/{\overline {WV}}}$, andernfalls gleich ${\displaystyle -{\overline {UW}}/{\overline {WV}}}$.

Betrachtet man nur die Streckenlängen, so kann man die obige Gleichung auch in folgender Form schreiben:

${\displaystyle {\overline {AZ}}\cdot {\overline {BX}}\cdot {\overline {CY}}={\overline {AY}}\cdot {\overline {BZ}}\cdot {\overline {CX}}}$

Da die Orientierung hierbei verloren geht, ist diese Gleichung nicht ausreichend für eine Umkehrung des Satzes, vgl. Satz von Ceva.

Zum Beweis des Satzes

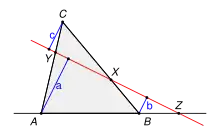
Der Satz von Menelaos lässt sich mit Hilfe des Strahlensatzes beweisen. Man betrachtet drei Lote auf die gegebene Gerade, die von den Ecken A, B und C ausgehen. Die Längen der Lotstrecken seien mit ${\displaystyle a}$, ${\displaystyle b}$ und ${\displaystyle c}$ bezeichnet.

Aus dem Strahlensatz erhält man folgende Verhältnisgleichungen:

${\displaystyle {\overline {AZ}}:{\overline {BZ}}=a:b}$

${\displaystyle {\overline {BX}}:{\overline {CX}}=b:c}$

${\displaystyle {\overline {CY}}:{\overline {AY}}=c:a}$

Multipliziert man diese drei Gleichungen miteinander, so ergibt sich

${\displaystyle {\frac {\overline {AZ}}{\overline {BZ}}}\cdot {\frac {\overline {BX}}{\overline {CX}}}\cdot {\frac {\overline {CY}}{\overline {AY}}}={\frac {a}{b}}\cdot {\frac {b}{c}}\cdot {\frac {c}{a}}={\frac {a\cdot b\cdot c}{b\cdot c\cdot a}}=1}$

und weiter (durch Multiplikation mit dem Nenner)

${\displaystyle {\overline {AZ}}\cdot {\overline {BX}}\cdot {\overline {CY}}={\overline {AY}}\cdot {\overline {BZ}}\cdot {\overline {CX}}}$.

Der Satz von Menelaos liefert zusammen mit seiner Umkehrung ein Kriterium für kollineare Punkte. Eine Folgerung ist der Satz von Ceva.

• Hans Schupp: Elementargeometrie. Schöningh, Paderborn 1977, ISBN 3-506-99189-2, S. 124 ff., S. 136 (Uni-Taschenbücher 669 Mathematik)
• Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3, S. 78–81
• Branko Grunbaum, G. C. Shephard: Ceva, Menelaus, and the Area Principle. In: Mathematics Magazine, Band 68, Nr. 4, Okt. 1995, S. 254–268 (JSTOR:2690569)

Commons: Menelaos's theorem – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Menelaus’ Theorem. In: MathWorld (englisch).
• Menelaos’ Theorem ein animierter, geometrischer Beweis des Satzes von Menelaos (englisch)
• Paul Yiu: Euclidean Geometry Notes (PDF; 1012 kB) Skript, Florida Atlantic University, S. 87–102