Satz von Hales-Jewett

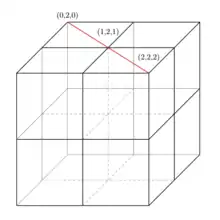
Mit ${\displaystyle C_{t}^{n}=\{(x_{1},\dots ,x_{n}):x_{i}\in [t]\}}$ bezeichnet man einen ${\displaystyle n}$-dimensionalen Würfel über ${\displaystyle t}$ Elementen. Als Linie in ${\displaystyle C_{t}^{n}}$ wird eine passend geordnete Menge von Punkten ${\displaystyle \mathbf {x} _{1},\dots \mathbf {x} _{t},\mathbf {x} _{i}=(x_{i1},\dots x_{in})}$ bezeichnet, so dass in jeder Koordinate ${\displaystyle 1\leq j\leq n}$ entweder

${\displaystyle x_{1j}=x_{2j}=\cdots =x_{tj}}$

oder

${\displaystyle x_{sj}=s}$ für ${\displaystyle 1\leq s<t+1}$

wobei letzteres mindestens einmal vorkommt, sonst wäre es nur ein Punkt. Beispielsweise ist ${\displaystyle \{1211,1222,1233,1244\}}$ eine Linie.

Als ${\displaystyle t}$-Färbung einer Menge ${\displaystyle T}$ bezeichnet man die Abbildung ${\displaystyle \chi :T\to [t]}$ und für ${\displaystyle s\in T}$ bezeichnet man ${\displaystyle \chi (s)}$ als Farbe. Man nennt ${\displaystyle M\subseteq T}$ monochromatisch falls ${\displaystyle \chi }$ konstant auf ${\displaystyle M}$ ist.

Für alle ${\displaystyle r,t}$ existiert ein ${\displaystyle HJ(r,t)}$, so dass für ${\displaystyle n\geq HJ}$ folgendes gilt: Falls die Knoten ${\displaystyle C_{t}^{n}}$ ${\displaystyle r}$-gefärbt sind, dann existiert eine monochromatische Linie.[1]