Remez-Algorithmus

Man beginnt mit den Extremstellen des Tschebyschow-Polynoms erster Art vom Grad ${\displaystyle n+1}$

${\displaystyle x_{i}={\frac {a+b}{2}}-{\frac {b-a}{2}}\cdot \cos \left({\frac {i\pi }{n+1}}\right)}$   mit   ${\displaystyle i=0,\ldots ,n+1}$.

Ein solcher Satz von Punkten wird „Referenz“[2] genannt. Es ist

${\displaystyle a=x_{0}<x_{1}<\,...\,<x_{n+1}=b}$.

Gesucht wird das Polynom ${\displaystyle p(x)}$ vom Grad ${\displaystyle \leq n}$, dessen Fehlerfunktion ${\displaystyle f(x)-p(x)}$ auf der im vorangegangenen Schritt gewonnenen Referenz ${\displaystyle x_{0}<x_{1}<\dots <x_{n+1}}$ alterniert. D. h. gesucht sind

${\displaystyle c_{0},c_{1},\ldots ,c_{n}}$   und   ${\displaystyle E}$.

mit

${\displaystyle p(x_{i})+(-1)^{i}\cdot E=f(x_{i})}$   für   ${\displaystyle i=0,\ldots ,n+1}$.

Diese Aufgabe hat als Eingabe nur die Referenz und von der Funktion ${\displaystyle f}$ nur die ${\displaystyle n+2}$ Werte ${\displaystyle f(x_{i})}$. Sie kann auch als Optimierungsaufgabe formuliert werden, nämlich als beste Approximation auf der Referenz, und ist eindeutig lösbar.

Das zu lösende Gleichungssystem in Matrixdarstellung:[3]

${\displaystyle \left({\begin{matrix}1&x_{0}&\cdots &x_{0}^{n}&1\\1&x_{1}&\cdots &x_{1}^{n}&-1\\\vdots &\vdots &\vdots &\vdots &\vdots \\1&x_{n}&\cdots &x_{n}^{n}&(-1)^{n}\\1&x_{n+1}&\cdots &x_{n+1}^{n}&(-1)^{n+1}\\\end{matrix}}\right){\begin{pmatrix}c_{0}\\c_{1}\\\vdots \\c_{n}\\E\end{pmatrix}}={\begin{pmatrix}f(x_{0})\\f(x_{1})\\\vdots \\f(x_{n})\\f(x_{n+1})\\\end{pmatrix}}}$

Damit hat man ${\displaystyle n+1}$ neue Koeffizienten

${\displaystyle c_{0},c_{1},\ldots ,c_{n}}$

für das Polynom ${\displaystyle p(x)}$ und eine neue »Referenzabweichung« ${\displaystyle E}$.

Finden lokale Extremstellen ${\displaystyle {\tilde {x}}_{1},{\tilde {x}}_{2}}$ der Fehlerfunktion ${\displaystyle 1/(37/12-x)-p(x)}$ mit ${\displaystyle {\color {Blue}p}}$ als einem Polynom vom Grad 2

Ausgehend vom Polynom ${\displaystyle p(x)}$ gilt es, ${\displaystyle n+2}$ Extremstellen ${\displaystyle {\tilde {x}}_{0},{\tilde {x}}_{1},\ldots ,{\tilde {x}}_{n+1}}$ der Fehlerfunktion

${\displaystyle f(x)-p(x)}$

zu finden. Ist ${\displaystyle f}$ differenzierbar, kann man Extremstellen oft durch Nullsetzen der Ableitungsfunktion ${\displaystyle f'-p'}$ gewinnen.

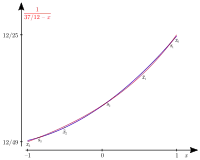
In jedem Fall lässt sich das Intervall ${\displaystyle [a,b]}$ in die durch die aktuelle Fehlerfunktion spezifizierbaren Teilintervalle ${\displaystyle [s_{i},s_{i+1}]}$ folgendermaßen aufteilen. Da mit ${\displaystyle f}$ auch ${\displaystyle f-p}$ stetig ist, gibt es nach dem Zwischenwertsatz für alle ${\displaystyle i=1,\ldots ,n+1}$ Nullstellen ${\displaystyle s_{i}}$ der Fehlerfunktion (in der Abbildung Schnittstellen der roten Funktion ${\displaystyle f}$ mit dem blauen Polynom ${\displaystyle p}$) im Intervall ${\displaystyle [x_{i-1},x_{i}]}$, da das Vorzeichen der Fehlerfunktion an den Stellen ${\displaystyle x_{i}}$ alterniert (${\displaystyle \operatorname {sgn}(f-p)(x_{i-1})=-\operatorname {sgn}(f-p)(x_{i})}$). Gibt es in zwei benachbarten Intervallen ${\displaystyle [x_{i-1},x_{i}]}$ und ${\displaystyle [x_{i},x_{i+1}]}$ jeweils nur eine Nullstelle ${\displaystyle s_{i}\in [x_{i-1},x_{i}]}$ beziehungsweise ${\displaystyle s_{i+1}\in [x_{i},x_{i+1}]}$, dann ist die Fehlerfunktion im Intervall ${\displaystyle [s_{i},s_{i+1}]}$ nur nicht-negativ oder nur nicht-positiv. (Aber auch wenn es mehrere Nullstellen gibt, gilt das Weitere – die Extrema sind ggf. nur nicht so ausgeprägt.) Wegen der Stetigkeit der Fehlerfunktion gibt es nach dem Satz vom Minimum und Maximum in jedem Teilintervall ${\displaystyle [s_{i},s_{i+1}]}$ (lokale) Extremstellen ${\displaystyle {\tilde {x}}_{i}}$. Im Ergebnis ist ${\displaystyle {\tilde {x}}_{0}:=a}$ das erste Extremum, die nachfolgenden Extrema alternieren zwischen Maximum und Minimum bis zum letzten Extremum ${\displaystyle {\tilde {x}}_{n+1}:=b}$.

Nebenbei fällt die (absolute) Güte der Approximation in Form von ${\displaystyle \max _{i}|f({\tilde {x}}_{i})-p({\tilde {x}}_{i})|}$ an. Ist sie unbefriedigend, kann man mit der neu gewonnenen Referenz ${\displaystyle {\tilde {x}}_{0},{\tilde {x}}_{1},\ldots ,{\tilde {x}}_{n+1}}$ iterieren. Es kann aber auch interessant sein, den Grad ${\displaystyle n}$ der Approximation durch Einfügen von Zwischenpunkten in die Referenz zu erhöhen. Das Beispiel 2 im Artikel Alternantensatz zeigt, wie die Qualität der dortigen besten Approximation vom Polynomgrad abhängt.

Unter geeigneten Voraussetzungen, die Funktion ${\displaystyle f}$ betreffend, konvergiert das Verfahren lokal quadratisch.[4]