Raumwinkel
Der Raumwinkel ist das dreidimensionale Gegenstück zum zweidimensionalen für die Ebene definierten Winkel. Er beschreibt den Anteil am gesamten dreidimensionalen Raum, der z. B. im Inneren eines gegebenen Kegel- oder Pyramidenmantels liegt.

Definition
Der Raumwinkel ist definiert als der Flächeninhalt einer messbaren Teilfläche einer Kugeloberfläche, dividiert durch das Quadrat des Radius der Kugel:
- .
Bei Betrachtung der Einheitskugel () ist also betragsgleich dem zugehörigen Raumwinkel. So ist der volle Raumwinkel gleich der Oberfläche der Einheitskugel, nämlich .
Die Teilfläche kann von beliebiger Umrissform sein. Vektoriell geschrieben als Flächenintegral ist
- .
Dabei ist der Einheitsvektor vom Koordinatenursprung, das differentielle Flächenelement und dessen Abstand vom Koordinatenursprung. Existiert dieses Integral, dann ist die Teilfläche messbar, und dies ist sowohl bei abgeschlossenen als auch offenen Teilmengen der Kugeloberfläche der Fall.
Anders als das Bild vielleicht vermuten lässt, spielt die Umrissform des Flächenstücks keine Rolle. Jede Umrissform auf der Kugeloberfläche mit dem gleichen Flächeninhalt definiert einen Raumwinkel der gleichen Größe. Legt man durch jeden Punkt der Umrissform einen Strahl mit dem Mittelpunkt der Kugel als Startpunkt, dann erhält man eine geometrische Figur, die den Raumwinkel veranschaulicht. Dies ist vergleichbar mit der Darstellung für einen Winkel in der Ebene: zwei Halbgeraden mit einem gemeinsamen Startpunkt.
Maßeinheiten
Obwohl der Raumwinkel eine Größe der Dimension Zahl ist, wird er zur Verdeutlichung meist in der Einheit Steradiant (sr) angegeben; dies entspricht dem Bogenmaß mit der Einheit Radiant (rad) beim ebenen Winkel. Ein Raumwinkel von 1 sr umschließt auf einer Kugel mit dem Radius 1 m eine Fläche von 1 m2. Da eine ganze Kugeloberfläche den Flächeninhalt hat, ist der zugehörige volle Raumwinkel
- .
Gelegentlich werden Raumwinkel auch in Quadratgrad, (°)², angegeben. 1 (°)² ist gleich .
Die Verwendung einer Hilfsmaßeinheit für eine Größe der Dimension Zahl hat, wie auf vielen Gebieten, insbesondere auch beim Raumwinkel, den Vorteil, dass schon an der verwendeten Einheit erkennbar ist, welche physikalische Größe gemeint ist. Die Lichtstärke (cd = lm/sr) zeigt im Gegensatz zum Lichtstrom (lm) ihre Abhängigkeit vom Raumwinkel durch das Auftreten des Steradiant in der Einheit. Die Lichtstärke bezeichnet somit einen vom Raumwinkel abhängigen Lichtstrom.
Darstellung mit Kugelkoordinaten

Der Raumwinkel eines Kugeldreiecks beträgt in Abhängigkeit von seinen Innenwinkeln Steradiant (siehe Kugeldreieck - Eigenschaften).
In einem Kugelkoordinatensystem kann der Raumwinkel besonders übersichtlich definiert werden, da es keine radiale Variable gibt. Zwei Meridianwinkel , und zwei Breitenwinkel , bestimmen ein Flächenelement auf einer Kugeloberfläche. Der zugehörige Raumwinkel beträgt:
Raumwinkel eines Kegels

Wählt man als Umrissform auf der Kugeloberfläche einen Kreis, so erhält man den kanonischen Raumwinkel. Der Raumwinkel bildet dann den Mantel eines geraden Kreiskegels, in dessen Spitze der Mittelpunkt der Kugel liegt.
Ist der Öffnungswinkel in der Spitze des Kegels, dann ergibt sich der Raumwinkel aus dem Doppelintegral[1]

| Öffnungswinkel in Grad | 0 | 1 | 2 | 5 | 10 | 15 | 30 | 45 | 57,2958 |
|---|---|---|---|---|---|---|---|---|---|
| Öffnungswinkel in Radiant | 0,0000 | 0,0175 | 0,0349 | 0,0873 | 0,1745 | 0,2618 | 0,5236 | 0,7854 | 1,0000 |
| Raumwinkel in Quadratgrad | 0,00 | 0,79 | 3,14 | 19,63 | 78,49 | 176,46 | 702,83 | 1570,10 | 2525,04 |
| Raumwinkel in Steradiant | 0,0000 | 0,0002 | 0,0010 | 0,0060 | 0,0239 | 0,0538 | 0,2141 | 0,4783 | 0,7692 |
| Öffnungswinkel in Grad | 60 | 65,5411 | 75 | 90 | 120 | 150 | 180 | 270 | 360 |
| Öffnungswinkel in Radiant | 1,0472 | 1,1439 | 1,3090 | 1,5708 | 2,0944 | 2,6180 | 3,1416 | 4,7124 | 6,2832 |
| Raumwinkel in Quadratgrad | 2763,42 | 3282,81 | 4262,39 | 6041,36 | 10313,24 | 15287,95 | 20626,48 | 35211,60 | 41252,96 |
| Raumwinkel in Steradiant | 0,8418 | 1,0000 | 1,2984 | 1,8403 | 3,1416 | 4,6570 | 6,2832 | 10,7261 | 12,5664 |
Raumwinkel einer rechteckigen Pyramide
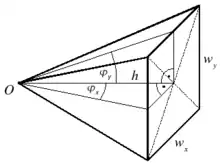
Der Spezialfall des Raumwinkels mit einem rechteckigen und ebenen Umriss entspricht der geometrischen Form einer Pyramide, wobei der Ursprung genau senkrecht über dem Mittelpunkt des ebenen Rechtecks stehe (siehe Abbildung). Dieser Raumwinkel tritt z. B. bei der Berechnung der Étendue von optischen Systemen mit rechteckigen Aperturen auf.
Er lässt sich sehr leicht mit der Oosterom-Strackee-Formel berechnen. Mit den Pyramidengrundseiten und sowie der Höhe h ergibt sich:
Verwendet man für die Berechnung die beiden Öffnungswinkel und , wobei und ist, so folgt nach einigen trigonometrischen Umformungen:
Beispiele:
Eine Rechteckblende vor einer Punktlichtquelle grenze den Lichtstrahl auf die Winkel 45° () und 20° () ein. Der Raumwinkel beträgt 0,27 sr.
Handelt es sich um eine quadratische Blende und sind beide Winkel 20° groß, dann umfasst der Raumwinkel 0,12 sr. Der kanonische Raumwinkel einer 20°-Kreisblende liegt bei 0,10 sr.
Raumwinkel von Polyedern
Formeln für Raumwinkel
Im Folgenden sind vier Punkte, so dass die Vektoren nicht in einer Ebene liegen (den Raum aufspannen), ist die Einheitskugel um und die Schnittpunkte der Geraden mit der Einheitskugel . bilden ein Tetraeder.
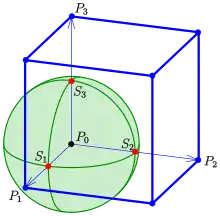
Ebenen-Formel
Die Winkel des sphärischen Dreiecks sind die Winkel zwischen den drei Ebenen, die durch die drei Punktetripel , , aufgespannt werden.
Der Flächeninhalt des sphärischen Dreiecks ist der Raumwinkel in der Tetraederecke (siehe oben)
Beispiel: Für sind die Winkel und der Raumwinkel im Nullpunkt gleich
Kanten-Formel
Der Raumwinkel in der Ecke eines Polyeders mit drei zusammentreffenden Seitenflächen (Polygonen) kann mit dem Satz von L’Huilier berechnet werden.[2]
Für den Raumwinkel, der in der Ecke mit den zusammentreffenden Innenwinkeln der drei Seitenflächen liegt, gilt
Beispiele: Für sind die Winkel und
Der Raumwinkel im Punkt ist (wie schon berechnet) gleich .
Für eine quadratische Pyramide mit den Winkeln in den Ecken der quadratischen Grundfläche gilt
In diesem Fall beträgt der Raumwinkel jeweils .
Richtungsvektoren-Formel
Sind die Vektoren Richtungsvektoren der Geraden , so gilt für den Raumwinkel
Dabei ist das Spatprodukt der Vektoren , und , ist das Skalarprodukt und ist die Länge des Vektors.
Diese Darstellung wurde im Jahr 1983 von Oosterom und Strackee[3] angegeben und bewiesen.
Beispiel: Für sind Richtungsvektoren. Mit für ergibt sich (wie schon berechnet)
Beispiele mit 3 Kanten an einer Ecke
Die drei Formeln zur Bestimmung des Raumwinkels können auf alle Polyederecken mit drei Kanten (Ebenen) angewandt werden.
Reguläres Tetraeder
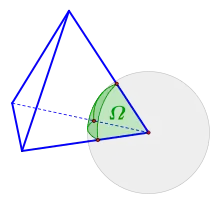
Bei einem regulären Tetraeder sind die Winkel zwischen den Seitenflächen und nach der Ebenen-Formel gilt
Die Kantenwinkel sind und damit gilt nach der Kanten-Formel
Gerades Prisma
Ein gerades Prisma besitzt ein Polygon als Grundfläche und zur Grundfläche senkrechte weitere Kanten (Ebenen). Ist der Winkel in einem Punkt des Grundflächenpolygons , so folgt aus der Ebenenformel, wegen der Orthogonalität der Seitenflächen, für den Raumwinkel in

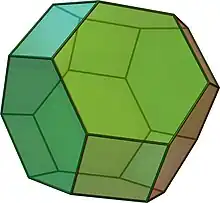
Oktaederstumpf

Ein Oktaederstumpf entsteht durch Beschneidung eines regulären Oktaeders. In einer Ecke treffen sich 3 Kanten und drei Ebenen, zwei reguläre Sechsecke und ein Quadrat. Es gibt also zwei Flächenwinkel: zwischen zwei Sechsecken und zwischen einem Sechseck und einem Quadrat. Es gilt (siehe Oktaederstumpf)
Damit ist nach der obigen Ebenenformel der Raumwinkel im Punkt
Die Innenwinkel, die an einer Basisecke zusammentreffen, sind . Aus der Kanten-Formel folgt daraus
Die Raumwinkel in den Ecken des Oktaederstumpfs sind also gleich des vollen Raumwinkels. Dieses Ergebnis wird dadurch bestätigt, dass sich der dreidimensionale euklidische Raum lückenlos mit kongruenten Oktaederstümpfen ausfüllen lässt, wobei in jeder Ecke 4 Oktaederstümpfe zusammentreffen (siehe Raumfüllung).
Beispiele mit mehr Kanten in einer Ecke
Gehen durch eine Polyederecke mehr als drei Kanten, hat man ein sphärisches Polygon mit mehr als drei Ecken. In vielen Fällen lässt sich das sphärische Polygon mit Hilfe eines inneren Hilfspunktes in sphärische Dreiecke zerlegen (analog zur Triangulierung eines ebenen konvexen Polygons).
Gerade quadratische Pyramide

Für eine gerade quadratische Pyramide mit der Quadratseitenlänge und Höhe ist der Winkel zwischen den Dreiecken
Schneidet man aus der Pyramide, wie aus einem Kuchen, entlang der Pyramidenhöhe und durch jeweils zwei benachbarte Basispunkte, erhält man eine Pyramide mit dreieckiger Grundfläche und einer Pyramidenkante an der Basis. Für den Raumwinkel an der Spitze der dreieckigen Pyramide ergibt sich
und der Raumwinkel der Pyramide an der Spitze ist
Der Winkel zwischen einem Dreieck und dem Quadrat ist
Mit der Ebenen-Formel ergibt sich für den Raumwinkel an einer Basisecke
Bemerkungen: Für ist diese Pyramide sozusagen ein halbes Oktaeder. In diesem Fall ist der Raumwinkel an der Spitze
- .
Der Raumwinkel an einer Basisecke, wo das Quadrat und zwei gleichseitige Dreiecke zusammentreffen, ist
- .
Dieser Winkel ist halb so groß wie der Raumwinkel an der Spitze, also gilt . Dies wird offensichtlich, wenn 2 dieser Pyramiden zu einem Oktaeder vervollständigt werden.
Die Innenwinkel, die an einer Basisecke zusammentreffen, sind . Aus der Kanten-Formel folgt daraus
mit dem gleichen Ergebnis. Die Umformungen ergeben sich mithilfe der Halbwinkelformeln, der Additionstheoreme für den Tangens und der Gleichungen , und .


Reguläres Ikosaeder
Die hier geschilderte Methode wird auch bei der Bestimmung des Raumwinkels eines regulären Ikosaeders angewandt. Bei einem Ikosaeder gehen durch jede Ecke fünf Kanten. Es wird der Raumwinkel einer Pyramide mit einem regulären Fünfeck als Basis bestimmt.
Weblinks
Einzelnachweise
- Oleg Mazonka: Solid Angle of Conical Surfaces, Polyhedral Cones, and Intersecting Spherical Caps
- Wolfram MathWorld: Spherical Excess
- A. Van Oosterom, J. Strackee: The Solid Angle of a Plane Triangle. In: Biomedical Engineering, IEEE Transactions on. BME-30, Nr. 2, 1983, S. 125–126, doi:10.1109/TBME.1983.325207.