Quantenalgorithmus

Das Modell für den Quantencomputer ist meistens eine Quantenschaltung. Eine Quantenschaltung verwendet Qubits anstelle von Bits. Der Zustand eines Quantenbits wird durch einen normierten Zustandsvektor mit den beiden Komponenten ${\displaystyle \alpha \left|0\right\rangle }$ und ${\displaystyle \beta \left|1\right\rangle }$ beschrieben. Das Betragsquadrat der beiden komplexen Amplituden ${\displaystyle \alpha }$ und ${\displaystyle \beta }$ bestimmt die Wahrscheinlichkeit, mit der der betreffende Messwert als Ergebnis einer Messung auftritt. Man fasst mehrere Qubits zu einem Quantenregister zusammen. Die Berechnung erfolgt durch die Anwendung von Quantengattern. Ein Quantengatter verändert den Zustand von einem oder mehreren Qubits. Im letzten Schritt liest man das Ergebnis aus. Dazu misst man einzelne Qubits. Die Messung zerstört Superpositionen bezüglich der Messbasis. Man kann nur den Zustand nach der Messung beobachten. Dieser Zustand wird von den Amplituden ${\displaystyle \alpha }$ und ${\displaystyle \beta }$ bestimmt.

Theoretisch kann man jeden klassischen Algorithmus so umformen, dass er auf diesem Modell ausgeführt werden kann (siehe Quantencomputer#Berechenbarkeit). Das hat allerdings keine praktischen Vorteile. Ein umgeformter klassischer Algorithmus benutzt auch auf einem Quantencomputer nur klassische Eigenschaften. Ein umgeformter klassischer Algorithmus wird nicht als Quantenalgorithmus bezeichnet.

Der einfachste Quantenalgorithmus ist ein Zufallszahlengenerator, der echte Zufallszahlen erzeugt. Ein klassischer Rechner kann nur Pseudozufallszahlen berechnen.

Der folgende Quantenalgorithmus erzeugt eine Zufallszahl mit den Werten 0 oder 1. Er verwendet ein Quantenregister mit einem Qubit, ein Quantengatter und eine Messung.[2]

1. Initialisiere das Quantenregister ${\displaystyle \left|x\right\rangle }$ mit dem Basiszustand ${\displaystyle \left|0\right\rangle }$:
   

   ${\displaystyle {\begin{aligned}\left|x\right\rangle &=\left|0\right\rangle \end{aligned}}}$

2. Wende ein Hadamard-Gatter auf das Quantenregister ${\displaystyle \left|x\right\rangle }$ an. Das Hadamard-Gatter erzeugt eine Superposition aus ${\displaystyle \left|0\right\rangle }$ und ${\displaystyle \left|1\right\rangle }$:
   

   ${\displaystyle {\begin{aligned}\left|x\right\rangle &\rightarrow H\left|x\right\rangle \\&={\frac {1}{\sqrt {2}}}{\bigl (}\left|0\right\rangle +\left|1\right\rangle {\bigr )}\\\end{aligned}}}$

3. Messe das Quantenregister. Das Ergebnis ${\displaystyle \left|0\right\rangle }$ tritt mit der Wahrscheinlichkeit 1/2 auf. Das Ergebnis ${\displaystyle \left|1\right\rangle }$ tritt ebenfalls mit der Wahrscheinlichkeit 1/2 auf.

Ein Qubit ist ein Zweizustands-Quantensystem. Das System wird nur durch die Quantenmechanik korrekt beschrieben. Es hat nur zwei durch Messung sicher unterscheidbare Zustände, nämlich die beiden Basiszustände der Messung. Der Zustand eines Qubits kann als Basiszustand einer geeignet gewählten Basis betrachtet werden, aber auch als Superpositionszustand von den Basisvektoren einer anderen Basis.

Beispiel: Die Superposition der Basiszustände ${\displaystyle \left|0\right\rangle }$ und ${\displaystyle \left|1\right\rangle }$ aus dem Beispiel für den Zufallszahlengenerator wird auch beschrieben als Basiszustand ${\displaystyle \left|+\right\rangle }$ einer Basis mit den Basiszuständen ${\displaystyle \left|+\right\rangle }$ und ${\displaystyle \left|-\right\rangle }$.

Ein Quantenalgorithmus kann in einem Rechenschritt mehr Werte „gleichzeitig“ verarbeiten als ein klassischer Computer, wenn der Zustand des Quantenregisters einer Superposition entspricht. Für die Quantenrechnung sind neben der Superposition auch die relative Phase (siehe Zustand (Quantenmechanik)#Phasenfaktor und Superposition) zwischen den beteiligten Komponenten und die Interferenz (siehe Interferenz (Physik)#Interferenz in der Quantenmechanik) zwischen ihnen von entscheidender Bedeutung.

Eine Messung hat die beiden Basiszustände der gewählten Messbasis als mögliches Ergebnis. Das Ergebnis einer einzelnen Messung ist genau dann deterministisch, wenn der Zustand des gemessenen Qubits einem der beiden Basiszustände der gewählten Messbasis entspricht. Wenn der Zustand des gemessenen Qubits eine Superposition von den Basisvektoren einer anderen Basis ist, dann kann man nur näherungsweise die Wahrscheinlichkeitsverteilung der beiden möglichen Messwerte bestimmen. Dazu muss man wiederholt dieselbe Superposition erzeugen und eine Messung daran durchführen und anschließend die Messergebnisse statistisch auswerten.

Deshalb hilft es oft wenig, wenn die Lösung einer Berechnung als Superposition vorliegt. Ein effizienter Quantenalgorithmus muss die Lösung in einen Zustand überführen, aus dem sie durch eine einzelne Messung oder durch wenige Wiederholungen des Ablaufs mit anschließender Messung sicher ausgelesen werden kann. Dabei spielen die Transformation der Zustände der Qubits in die gewählte Messbasis bzw. die Interferenz eine wichtige Rolle.[3]

Beispiel: Es ist nicht möglich, durch Messen in der Standard-Basis ${\displaystyle \left|0\right\rangle }$ und ${\displaystyle \left|1\right\rangle }$ einen Unterschied zwischen den Zuständen ${\displaystyle \left|+\right\rangle }$ und ${\displaystyle \left|-\right\rangle }$ zu erkennen. Erst nach Anwendung des Hadamard-Gatters ergibt eine Messung eindeutig ${\displaystyle \left|0\right\rangle }$ oder ${\displaystyle \left|1\right\rangle }$. Das liegt daran, dass das Hadamard-Gatter die beiden Zustände ${\displaystyle \left|+\right\rangle }$ und ${\displaystyle \left|-\right\rangle }$ in die Standard-Basis transformiert. Eine andere Formulierung dafür ist, dass das Hadamard-Gatter den Anteil in Richtung des einen Basis-Zustands durch Interferenz verstärkt und den Anteil in Richtung des anderen Basis-Zustands durch Interferenz auslöscht.[4]

Qubits in Superposition können miteinander verschränkt sein. Wenn zwei Qubits maximal miteinander verschränkt sind, enthält der Zustand der einzelnen Qubits keine Information. Die Information über die Korrelation der beiden Qubits und die Wahrscheinlichkeitsverteilung der Messergebnisse findet sich nur in der Beschreibung für den Gesamtzustand des Paars.[5]

Beispiel: siehe Bell-Zustand

Phase-Kickback ist ein Mechanismus, den die meisten Quantenalgorithmen benutzen. Phase-Kickback tritt z. B. auf, wenn bei einem CNOT-Gatter das Steuer-Qubit in Superposition ${\displaystyle \left|+\right\rangle }$ und das Ziel-Qubit in Superposition ${\displaystyle \left|-\right\rangle }$ ist. Dann dreht das CNOT-Gatter die relative Phase des Steuer-Qubits um 180 Grad. Das Ziel-Qubit wird dabei nicht verändert.[6] Mit anderen Worten: im Beispiel wechselt das Vorzeichen der Amplitude des Steuerqubits bzw. die Amplitude kippt.

1. Initialisiere das Quantenregister wie folgt:
   

   ${\displaystyle {\begin{aligned}\left|x\right\rangle \left|y\right\rangle &=\left|0\right\rangle \left|1\right\rangle \\&=\left|a\right\rangle \end{aligned}}}$

2. Wende das Hadamard-Gatter ${\displaystyle H}$ auf beide Qubits an:
   

   ${\displaystyle {\begin{aligned}\left|x\right\rangle \left|y\right\rangle &\rightarrow H\left|x\right\rangle H\left|y\right\rangle \\&={\frac {1}{\sqrt {2}}}{\bigl (}\left|0\right\rangle +\left|1\right\rangle {\bigr )}\cdot {\frac {1}{\sqrt {2}}}{\bigl (}\left|0\right\rangle -\left|1\right\rangle {\bigr )}\\&={\frac {1}{2}}{\bigl (}\left|0\right\rangle \left|0\right\rangle -\left|0\right\rangle \left|1\right\rangle +\left|1\right\rangle \left|0\right\rangle -\left|1\right\rangle \left|1\right\rangle {\bigr )}\\&=\left|b\right\rangle =\left|+\right\rangle \left|-\right\rangle \end{aligned}}}$

3. Wende das CNOT-Gatter an mit ${\displaystyle x}$ als Steuer-Qubit und ${\displaystyle y}$ als Ziel-Qubit

   ${\displaystyle {\begin{aligned}\left|x\right\rangle \left|y\right\rangle &\rightarrow \ CNOT\left|x\right\rangle \left|y\right\rangle \\&={\frac {1}{2}}{\bigl (}\left|0\right\rangle \left|0\right\rangle -\left|0\right\rangle \left|1\right\rangle +\left|1\right\rangle \left|1\right\rangle -\left|1\right\rangle \left|0\right\rangle {\bigr )}\\&={\frac {1}{2}}{\bigl (}\left|0\right\rangle \left|0\right\rangle -\left|0\right\rangle \left|1\right\rangle -\left|1\right\rangle \left|0\right\rangle +\left|1\right\rangle \left|1\right\rangle {\bigr )}\\&=\left|c\right\rangle =\left|-\right\rangle \left|-\right\rangle \end{aligned}}}$

Wenn man die Zustände ${\displaystyle \left|b\right\rangle }$ und ${\displaystyle \left|c\right\rangle }$ miteinander vergleicht, sieht man, dass das CNOT-Gatter den Zustand des Ziel-Qubits ${\displaystyle y}$ nicht verändert hat. Stattdessen hat es die relative Phase des Steuer-Qubits ${\displaystyle x}$ um 180 Grad gedreht.

Diesen Mechanismus nennt man Phase-Kickback. Der Deutsch-Jozsa-Algorithmus benutzt ihn, um mit einem einzigen Aufruf des Orakels eine bestimmte Eigenschaft zu erkennen, während ein klassischer Algorithmus dafür mehrere Aufrufe benötigt. Der Grover-Algorithmus benutzt Phase-Kickback bei der Amplitudenverstärkung.

Amplitudenverstärkung, erster Durchlauf: in blau die Amplituden nach Phase-Kickback für die Lösung „6“, in grün die Amplituden nach Spiegelung an der roten Achse

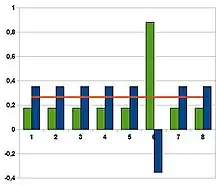
Die Amplitudenverstärkung (engl. amplitude amplification) wird z. B. im Grover-Algorithmus angewendet. Nach Herstellen einer gleichmäßigen Superposition wechselt der Grover-Algorithmus mit Phase-Kickback das Vorzeichen der Amplitude der Lösung und vergrößert danach den Betrag dieser Amplitude durch Spiegelung. Das wiederholt der Algorithmus so oft, bis die Lösung mit sehr großer Wahrscheinlichkeit durch eine Messung ausgelesen werden kann.[7]

Allgemeine Formulierung zur Berechnung einer Lösung:

1. Beginne mit der gleichmäßigen Superposition aller möglichen Lösungen
2. Führe wiederholt Schritte aus, die den Betrag der Amplitude der Lösung vergrößern und gleichzeitig die Beträge der anderen Amplituden verkleinern

Ein Orakel ist eine Black-Box. Allgemein formuliert verwendet ein Quantenorakel ein oder mehrere Eingabebits ${\displaystyle \left|x\right\rangle }$, ein Orakelbit ${\displaystyle \left|y\right\rangle }$ und bei Bedarf ein oder mehrere Hilfsbits ${\displaystyle \left|z\right\rangle }$.

${\displaystyle U_{f}:\left|x\right\rangle \left|y\right\rangle \left|z\right\rangle \mapsto \left|x\right\rangle \left|f(x)\oplus y\right\rangle \left|z\right\rangle }$[9]

• Der Deutsch-Jozsa-Algorithmus konnte als erster Quantenalgorithmus zeigen, dass er eine bestimmte Eigenschaft der Orakel-Funktion mit weniger Zugriffen auf das Orakel erkennen kann als klassische Algorithmen. Dadurch konnte er das Potential von Quantencomputern deutlich machen.
• Der Grover-Algorithmus hat diesen Ansatz weiter entwickelt. Der Grover-Algorithmus wurde ursprünglich für die Suche in Datenbanken entworfen. Er kann aber ganz allgemein Probleme lösen, deren Lösung durch eine Orakel-Funktion beschrieben werden kann. Bei der Suche in einer unsortierten Datenbank muss sich ein klassischer Computer bei ${\displaystyle n}$ Einträgen im schlimmsten Fall alle Einträge ansehen (d. h. vergleichen), klassisch ist dieses Problem also in ${\displaystyle {\mathcal {O}}(n)}$ Rechenschritten lösbar. Auf einem Quantencomputer kann man dies mit dem Grover-Algorithmus in lediglich ${\displaystyle {\mathcal {O}}\left({\sqrt {n}}\right)}$ Operationen erledigen. Diese Schranke ist scharf, das heißt, kein Quantenalgorithmus kann dieses Problem in (asymptotisch) weniger Operationen lösen. Daraus folgt, dass für diese Art von Problemen kein exponentieller Geschwindigkeitsvorteil bei Verwendung von Quantenalgorithmen zu erwarten ist.
• Simons Algorithmus konnte als erster Algorithmus einen exponentiellen Vorteil im Vergleich zu dem besten klassischen Algorithmus zeigen. Das Problem besteht darin, zu erkennen, ob eine gegebene Orakel-Funktion die Eingabewerte eins-zu-eins oder zwei-zu-eins abbildet. Eins-zu-eins bildet jede Eingabe auf eine eindeutige Ausgabe ab. Zwei-zu-eins bildet je zwei Eingaben auf dieselbe Ausgabe ab. Er hat, wie auch der Deutsch-Josza-Algorithmus, keinen großen praktischen Nutzen. Er inspirierte aber zur Entwicklung von Quantenalgorithmen, die auf der Quanten-Fouriertransformation basieren, wie dem Shor-Algorithmus.[10]

Der wohl berühmteste Algorithmus für Quantencomputer ist der Shor-Algorithmus zur Faktorisierung großer ganzer Zahlen. Er spielt für die Primzahlzerlegung in der Kryptographie eine wichtige Rolle. Der Zeitaufwand ist dabei polynomiell in der Anzahl der Ziffern. Im Gegensatz dazu benötigt der beste zurzeit bekannte klassische Algorithmus, das Zahlkörpersieb, superpolynomiell (aber subexponentiell) viel Zeit. Die Bedeutung von Shors Algorithmus beruht auf der Tatsache, dass die Sicherheit der asymmetrischen Verschlüsselungsverfahren wie RSA darauf basiert, dass keine hinreichend effizienten klassischen Algorithmen zur Faktorisierung großer Zahlen bekannt sind.

Für die Untersuchung von quantenmechanischen Systemen bietet es sich an, sie in der gut kontrollierbaren Umgebung einer Quantenschaltung zu simulieren. Algorithmen dieser Art erlauben z. B. die Untersuchung von Abläufen in der Quantenchemie.[11]

Im Bereich Maschinelles Lernen entscheidet oft ein Algorithmus darüber, zu welcher von zwei Klassen ein gegebener Datenpunkt gehört. Dazu wird in der Lernphase der Verlauf einer Trennlinie berechnet, die die Datenpunkte der beiden Klassen voneinander trennt. Ein klassisches Verfahren für das Berechnen der Trennlinie ist die Support Vector Machine. Das Verfahren liefert für ausgewählte Datensätze nur ungenaue Ergebnisse, d. h., es werden relativ viele Datenpunkte der falschen Klasse zugeordnet. Es wurden Quantenalgorithmen entwickelt (Stichworte: Quantum Support Vector Machine und Quantum Kernel Estimation), die die Trennlinie für diese Datensätze schneller und genauer berechnen können.[12]

Als Quantenschlüsselaustausch bezeichnet man Verfahren der Quantenkryptografie, die Eigenschaften der Quantenmechanik nutzen, um zwei Parteien eine gemeinsame Zufallszahl zur Verfügung zu stellen. Diese Verfahren setzen auch den Algorithmus zur Erzeugung von Zufallszahlen ein.

• BB84-Protokoll
• Ekert-Protokoll

Quantenfehlerkorrektur wird benutzt, um Fehler infolge von Dekohärenz zu beheben. Quantenfehlerkorrekturen sind grundlegend beim Ausführen von fehlertoleranten Quantenberechnungen.