Primzahlsatz

Im Weiteren sei ${\displaystyle \pi (x)}$ die Primzahlfunktion, die für beliebige reelle Zahlen ${\displaystyle x}$ definiert ist als die Anzahl der Primzahlen, die nicht größer als ${\displaystyle x}$ sind. Formal kann man schreiben:

${\displaystyle \pi (x):=\left|\{p\in \mathbb {P} \mid p\leq x\}\right|}$

Dabei bezeichnet das Symbol ${\displaystyle \mathbb {P} }$ die Menge der Primzahlen, die Schreibweise ${\displaystyle \left|M\right|}$ steht für die Anzahl der Elemente der Menge ${\displaystyle M.}$

Der Primzahlsatz besagt:

${\displaystyle \lim _{x\to \infty }{\frac {\pi (x)}{\frac {x}{\ln(x)}}}=1}$

Nennt man zwei reelle Funktionen ${\displaystyle f}$ und ${\displaystyle g}$ asymptotisch äquivalent, wenn der Quotient ${\displaystyle {\tfrac {f(x)}{g(x)}}}$ für ${\displaystyle x\to \infty }$ gegen 1 konvergiert, so kann man den Primzahlsatz auch so formulieren: Die Funktionen ${\displaystyle \pi (x)}$ und ${\displaystyle {\tfrac {x}{\ln(x)}}}$ sind asymptotisch äquivalent, geschrieben ${\displaystyle \pi (x)\sim {\tfrac {x}{\ln(x)}}}$.

Der Primzahlsatz ist im Wesentlichen äquivalent dazu, dass die Riemannsche Zetafunktion keine Nullstellen ${\displaystyle s}$ mit ${\displaystyle \operatorname {Re} (s)\geq 1}$ hat.

Es gibt verschiedene analytische Beweise. Ein einfacher Beweis, der die Abschätzung der Zetafunktion im Unendlichen nach Hadamard und La Vallée Poussin vermeidet, wurde von Donald Newman gegeben.[1][2] Ein dritter Weg innerhalb der analytischen Zahlentheorie benutzt die Taubersätze von Wiener-Ikehara, vermeidet ebenfalls die Abschätzung im Unendlichen, benutzt aber tieferliegende Ergebnisse aus der Theorie der Fourier-Transformation. Es gibt auch Beweise ohne Verwendung komplexer Funktionentheorie („elementare“ Beweise nach Paul Erdős und Atle Selberg).

Darstellung von π(x) (rot), x/ln(x) (grün) und Li(x) (blau)

Bessere Approximationen als ${\displaystyle {\tfrac {x}{\ln(x)}}}$ liefert der Integrallogarithmus

${\displaystyle \mathrm {Li} (x):=\int _{2}^{x}{\frac {\mathrm {d} t}{\ln t}}.}$

Die Integraldarstellung für ${\displaystyle \operatorname {Li} (x)}$ wird gewählt, weil die Stammfunktionen von ${\displaystyle 1/\ln(x)}$ nicht elementar sind.

Der Integrallogarithmus ist asymptotisch äquivalent zu ${\displaystyle x/{\ln(x)},}$ also auch zu ${\displaystyle \pi (x).}$

Man kann zeigen:[3]

${\displaystyle \pi (x)=\mathrm {Li} (x)+O\left(x\cdot \exp(-C(\ln(x))^{3/5}(\ln \ln(x))^{-1/5})\right)}$

mit einer positiven Konstanten ${\displaystyle C}$. Dabei ist ${\displaystyle O(\cdot )}$ ein Landau-Symbol, d. h., es gibt eine Konstante ${\displaystyle D}$, sodass

${\displaystyle {\Big |}\pi (x)-\mathrm {Li} (x){\Big |}<D\cdot x\cdot \exp \left(-C(\ln(x))^{3/5}(\ln \ln(x))^{-1/5}\right)}$

für alle ${\displaystyle x}$ gilt. Die Verbesserung des Fehlerterms hängt davon ab zu zeigen, dass die Zetafunktion in immer größeren Bereichen im kritischen Streifen nullstellenfrei ist. Unter Annahme der Riemannschen Vermutung (nach der alle nicht-trivialen Nullstellen auf der Geraden ${\displaystyle s={\tfrac {1}{2}}}$ liegen), und nur unter dieser, kann man die Fehlerabschätzung zu

${\displaystyle \pi (x)=\mathrm {Li} (x)+O\left({\sqrt {x}}\cdot \ln(x)\right)}$

verbessern (Helge von Koch 1901). Eine nicht-asymptotische Schranke fand Lowell Schoenfeld unter Annahme der Riemann-Vermutung:[4]

${\displaystyle {\big |}\pi (x)-\mathrm {Li} (x){\big |}<{\frac {{\sqrt {x}}\ln x}{8\pi }}}$.

Adrien-Marie Legendre veröffentlichte 1798 als erster in seiner Théorie des nombres (Abhandlung über Zahlentheorie) unabhängig von Gauß[5] den vermuteten Zusammenhang zwischen Primzahlen und Logarithmen. In der zweiten Auflage dieses Werks 1808 verbesserte er die Abschätzung von ${\displaystyle \pi (x)}$ zu ungefähr gleich[6]

${\displaystyle {\frac {x}{\ln(x)-1{,}08366}}}$

(wo dieser Wert 1,08366 verantwortlich für das Problem der Existenz der Legendre-Konstanten ist). Ein erster Schritt hin zu einem Beweis gelang Pafnuti Lwowitsch Tschebyschow, der 1851 die folgende schwächere Form des Primzahlsatzes zeigte:[7][8]

${\displaystyle 0{,}92929\leq {\frac {\pi (x)}{\frac {x}{\ln(x)}}}\leq 1{,}1056}$

für alle hinreichend großen ${\displaystyle x}$. Das heißt, dass die Anzahl der Primzahlen unter einer gegebenen Größe um nicht mehr als ungefähr 10 % nach oben oder unten von der logarithmischen Funktion ${\displaystyle x/\ln(x)}$ abweicht.

Der englische Mathematiker James Joseph Sylvester, damals Professor an der amerikanischen Johns Hopkins University in Baltimore, verfeinerte 1892 Tschebyschows Methode und zeigte, dass für die Ungleichung bei hinreichend großem ${\displaystyle x}$ die untere Grenze 0,95695 und die obere Grenze 1,04423 genügt,[9] die Abweichung also maximal nur mehr ungefähr 5 % beträgt.

In seiner berühmten Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe (1859) hat Bernhard Riemann den Zusammenhang zwischen der Verteilung der Primzahlen und den Eigenschaften der Riemannschen Zetafunktion gezeigt.[10] Der deutsche Mathematiker Hans von Mangoldt bewies 1895 das Hauptresultat der Riemannschen Arbeit, dass der Primzahlsatz dem Satz äquivalent ist, dass die Riemannsche Zetafunktion keine Nullstellen mit Realteil 1 hat.[11] Sowohl Hadamard als auch de la Vallée Poussin haben 1896 die Nichtexistenz solcher Nullstellen bewiesen.[12][13][14] Ihre Beweise des Primzahlsatzes sind also nicht „elementar“, sondern verwenden funktionentheoretische Methoden. Lange Jahre galt ein elementarer Beweis des Primzahlsatzes für unmöglich, was 1949 durch die von Atle Selberg und Paul Erdős gefundenen Beweise widerlegt wurde (wobei „elementar“ hier keineswegs „einfach“ bedeutet).[15][16][17] Später wurden noch zahlreiche Varianten und Vereinfachungen dieser Beweise gefunden.

Die folgende Tabelle zeigt konkrete Werte der Primzahlfunktion im Vergleich mit den Logarithmen, Legendres Formel und dem Integrallogarithmus.[18][19][20]

${\displaystyle x}$	${\displaystyle \pi (x)}$	${\displaystyle {\frac {\pi (x)}{x}}\approx }$	${\displaystyle {\frac {x}{\ln(x)}}\approx }$	${\displaystyle \pi (x)-{\frac {x}{\ln(x)}}\approx }$	${\displaystyle {\frac {\pi (x)}{\frac {x}{\ln(x)}}}\approx }$	${\displaystyle {\frac {x}{\ln(x)-1{,}08366}}\approx }$	${\displaystyle \mathrm {Li} (x):=\int _{2}^{x}{\frac {\mathrm {d} t}{\ln t}}\approx }$	${\displaystyle \mathrm {Li} (x)-\pi (x)\approx }$
10	4	0,400000	4	0	0,921034	8	6	2
102	25	0,250000	22	3	1,151293	28	30	5
103	168	0,168000	145	23	1,160503	172	178	10
104	1.229	0,122900	1.086	143	1,131951	1.231	1.246	17
105	9.592	0,095920	8.686	906	1,104320	9.588	9.630	38
106	78.498	0,078498	72.382	6.116	1,084490	78.543	78.628	130
107	664.579	0,066458	620.421	44.158	1,071175	665.140	664.918	339
108	5.761.455	0,057615	5.428.681	332.774	1,061299	5.768.004	5.762.209	754
109	50.847.534	0,050848	48.254.942	2.592.592	1,053727	50.917.519	50.849.235	1.701
1010	455.052.511	0,045505	434.294.482	20.758.029	1,047797	455.743.004	455.055.615	3.104
1011	4.118.054.813	0,041181	3.948.131.654	169.923.159	1,043039	4.124.599.869	4.118.066.401	11.588
1012	37.607.912.018	0,037608	36.191.206.825	1.416.705.193	1,039145	37.668.527.415	37.607.950.281	38.263
1013	346.065.536.839	0,034607	334.072.678.387	11.992.858.452	1,035899	346.621.096.885	346.065.645.810	108.971
1014	3.204.941.750.802	0,032049	3.102.103.442.166	102.838.308.636	1,033151	3.210.012.022.164	3.204.942.065.692	314.890
1015	29.844.570.422.669	0,029845	28.952.965.460.217	891.604.962.452	1,030795	29.890.794.226.982	29.844.571.475.288	1.052.619
1016	279.238.341.033.925	0,027924	271.434.051.189.532	7.804.289.844.393	1,028752	279.660.033.612.131	279.238.344.248.557	3.214.632
1017	2.623.557.157.654.233	0,026236	2.554.673.422.960.305	68.883.734.693.281	1,026964	2.627.410.589.445.923	2.623.557.165.610.822	7.956.589
1018	24.739.954.287.740.860	0,024740	24.127.471.216.847.324	612.483.070.893.536	1,025385	24.775.244.142.175.635	24.739.954.309.690.415	21.949.555
1019	234.057.667.276.344.607	0,023406	228.576.043.106.974.646	5.481.624.169.369.960	1,023982	234.381.646.366.460.804	234.057.667.376.222.382	99.877.775
1020	2.220.819.602.560.918.840	0,022208	2.171.472.409.516.259.138	49.347.193.044.659.701	1,022725	2.223.801.523.570.829.204	2.220.819.602.783.663.484	222.744.644
1021	21.127.269.486.018.731.928	0,021127	20.680.689.614.440.563.221	446.579.871.578.168.707	1,021594	21.154.786.057.670.023.133	21.127.269.486.616.126.182	597.394.254
1022	201.467.286.689.315.906.290	0,020147	197.406.582.683.296.285.296	4.060.704.006.019.620.994	1,020570	201.721.849.105.666.574.218	201.467.286.691.248.261.498	1.932.355.208
1023	1.925.320.391.606.803.968.923	0,019253	1.888.236.877.840.225.337.614	37.083.513.766.578.631.309	1,019639	1.927.681.221.597.738.628.080	1.925.320.391.614.054.155.139	7.250.186.216
1024	18.435.599.767.349.200.867.866	0,018436	18.095.603.412.635.492.818.797	339.996.354.713.708.049.069	1,018789	18.457.546.327.619.878.007.916	18.435.599.767.366.347.775.144	17.146.907.278
1025	176.846.309.399.143.769.411.680	0,017685	173.717.792.761.300.731.060.452	3.128.516.637.843.038.351.228	1,018009	177.050.792.039.110.236.839.710	176.846.309.399.198.930.392.619	55.160.980.939
1026	1.699.246.750.872.437.141.327.603	0,016992	1.670.363.391.935.583.952.504.342	28.883.358.936.853.188.823.261	1,017292	1.701.156.120.834.278.630.173.694	1.699.246.750.872.593.033.005.724	155.891.678.121
1027	16.352.460.426.841.680.446.427.399	0,016352	16.084.980.811.231.549.172.264.034	267.479.615.610.131.274.163.365	1,016629	16.370.326.243.373.272.895.062.280	16.352.460.426.842.189.113.085.405	508.666.658.006
1028	157.589.269.275.973.410.412.739.598	0,015759	155.105.172.108.304.224.161.117.471	2.484.097.167.669.186.251.622.127	1,016016	157.756.767.911.194.258.241.759.313	157.589.269.275.974.838.158.399.972	1.427.745.660.374
1029	1.520.698.109.714.272.166.094.258.063	0,015207	1.497.567.178.976.730.440.176.306.617	23.130.930.737.541.725.917.951.446	1,015446	1.522.271.416.204.882.045.821.506.579	1.520.698.109.714.276.717.287.880.527	4.551.193.622.464
OEIS	Folge A006880 in OEIS		Folge A057834 in OEIS	Folge A057835 in OEIS		Folge A058289 in OEIS	Folge A057754 in OEIS	Folge A057752 in OEIS

Die Größe ${\displaystyle \pi (x)/x}$ heißt Primzahldichte.

Vergleicht man ${\displaystyle \operatorname {Li} (x)}$ mit den Werten von ${\displaystyle \pi (x)}$ in der Tabelle, scheint es so, als ob stets ${\displaystyle \operatorname {Li} (x)>\pi (x)}$ gelten würde. Tatsächlich wechselt die Differenz ${\displaystyle \mathrm {Li} (x)-\pi (x)}$ bei größer werdendem ${\displaystyle x}$ das Vorzeichen unendlich oft, wie J. E. Littlewood 1914 zeigen konnte.[21] Die gaußsche Formel unterschätzt also die Anzahl der Primzahlen in einem hinreichend großen Zahlenbereich, den Stanley Skewes 1933 mit der nach ihm benannten Skewes-Zahl nach oben abschätzen konnte.[22] Russell Sherman Lehman stellte 1966 einen wichtigen Satz über die obere Grenze auf und konnte sie auf eine „handhabbare“ Größe von 1,165·10¹¹⁶⁵ drücken.[23] Unter Verwendung des Lehmanschen Satzes gelang es dem niederländischen Mathematiker Herman te Riele 1986 zu zeigen, dass es zwischen 6,627·10³⁷⁰ und 6,687·10³⁷⁰ mehr als 10¹⁸⁰ aufeinanderfolgende Zahlen ${\displaystyle x}$ gibt, für die ${\displaystyle \pi (x)>\mathrm {Li} (x)}$ gilt.[24] Den derzeit besten untersten Wert, ebenfalls ausgehend von den Ergebnissen Lehmans, ermittelten im Jahr 2000 die beiden Mathematiker Carter Bays und Richard Hudson, die zeigten, dass ein solcher von Littlewood bewiesener Wechsel vor 1,398244·10³¹⁶ auftritt.[25] Obwohl sie nicht beweisen konnten, damit tatsächlich den ersten Vorzeichenwechsel gefunden zu haben, legen ihre Berechnungen dies nahe. Genauer vermuten sie, dass die Ungleichung ${\displaystyle \pi (x)<\mathrm {Li} (x)}$ für ${\displaystyle x<1{,}398\cdot 10^{316}}$ immer gilt.

Formeln für Primzahlfunktionen gibt es in zwei Arten: arithmetische Formeln und analytische Formeln. Analytische Formeln für die Primzahlenzählung waren die ersten, die verwendet wurden, um den Primzahlsatz zu beweisen. Sie stammen aus der Arbeit von Bernhard Riemann und Hans von Mangoldt und sind allgemein als explizite Formeln bekannt.[26]

Wir haben folgenden Ausdruck für ${\displaystyle \psi }$:

${\displaystyle \psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\ln 2\pi -{\frac {1}{2}}\ln(1-x^{-2})}$

wobei

${\displaystyle \psi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.}$

und ${\displaystyle \psi (x)}$ der zweiten Tschebyschow-Funktion. Hier sind ${\displaystyle \rho }$ die Nullstellen der Riemannschen Zetafunktion im kritischen Streifen, bei dem der Realteil von ${\displaystyle \rho }$ zwischen Null und Eins liegt. Die Formel gilt für Werte von ${\displaystyle x}$ größer als eins, d. h. die Region von Interesse. Die Summe über den Wurzeln ist bedingt konvergent und sollte in der Reihenfolge zunehmender Absolutwerte des Imaginärteils genommen werden. Zu beachten ist, dass die gleiche Summe über die trivialen Wurzeln den letzten Subtrahenden in der Formel ergibt.

Ähnlich wie für ${\displaystyle \psi }$ kann auch für die von Riemann eingeführte Primzahlen abzählende Funktion ${\displaystyle \Pi (x)}$ [27] eine Mittelung an den Sprungstellen ${\displaystyle \Pi _{0}(x)}$ eingeführt werden. Für ${\displaystyle \Pi _{0}(x)}$ haben wir die kompliziertere Formel

${\displaystyle \Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\ln 2+\int _{x}^{\infty }{\frac {\mathrm {d} t}{t(t^{2}-1)\ln t}}.}$

Auch hier gilt die Formel wieder für ${\displaystyle x>1}$, während ${\displaystyle \rho }$ die nicht-trivialen Nullstellen der Riemannschen Zetafunktion nach ihrem Absolutwert geordnet sind, und letzteres Integral wiederum mit Minuszeichen genommen ist genau die gleiche Summe, aber über den trivialen Nullstellen. Der erste Ausdruck ${\displaystyle \operatorname {li} (x)}$ ist die übliche logarithmische Integralfunktion; der Ausdruck ${\displaystyle \operatorname {li} (x^{\rho })}$ im zweiten Term sollte als ${\displaystyle \operatorname {Ei} (\rho \ln x)}$ betrachtet werden, wobei ${\displaystyle \operatorname {Ei} }$ die analytische Fortsetzung der exponentiellen Integralfunktion von der positiven Realen zur komplexen Ebene mit entlang der negativen Realen Achse geschnittenem Ast ist.

Somit ergibt sich wenn man wie oben eine an den Sprungstellen mittelnde Funktion ${\displaystyle \pi _{0}(x)={\frac {1}{2}}\lim _{\varepsilon \to 0}(\pi (x+\varepsilon )+\pi (x-\varepsilon ))}$ einführt mit der Möbius-Inversionsformel[28]

${\displaystyle \pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho })-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}}$

gültig für ${\displaystyle x>1}$, wobei

${\displaystyle \operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k!k\zeta (k+1)}}}$

die sogenannte Riemannsche R-Funktion ist.[29] Die letztgenannte Reihe dafür ist bekannt als Gram-Reihe[30] und konvergiert für alle positiven ${\displaystyle x}$. ${\displaystyle \mu (n)}$ ist die Möbius-Funktion und ${\displaystyle \zeta (z)}$ die riemannsche Zetafunktion.

Δ-Funktion (rote Linie) auf Log-Skala

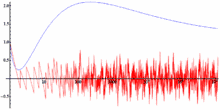
Die Summe über nichttriviale Nullstellen der Zetafunktion in der Formel für ${\displaystyle \pi _{0}(x)}$ beschreibt die Schwankungen von ${\displaystyle \pi _{0}(x)}$, während die restlichen Terme den „glatten“ Teil der Primzahlfunktion ausmachen.[31]

Somit kann man

${\displaystyle \operatorname {R} (x)-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}}$

als den besten Fit der ${\displaystyle \pi (x)}$ für ${\displaystyle x>1}$ bezeichnen.

Die Amplitude des „verrauschten“ Teils liegt heuristisch bei ca. ${\displaystyle {\sqrt {x}}/\ln x}$, womit die Schwankungen der Primzahlenverteilung mit der ${\displaystyle \Delta }$-Funktion dargestellt werden können:

${\displaystyle \Delta (x)=\left(\pi _{0}(x)-\operatorname {R} (x)+{\frac {1}{\ln x}}-{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}\right){\frac {\ln x}{\sqrt {x}}}.}$

Eine umfangreiche Tabelle mit den Werten von ${\displaystyle \Delta (x)}$ steht zur Verfügung.[32]

Der Primzahlsatz gibt auch Auskunft über die aufsteigende Folge ${\displaystyle (p_{n})=2,3,5,\dotsc }$ der Primzahlen. So ist er äquivalent zu der Aussage

${\displaystyle p_{n}\sim n\ln(n)}$

und es gilt sogar für alle ${\displaystyle n\geq 6:}$[33]

${\displaystyle \ln(n)+\ln \ln(n)-1<{\frac {p_{n}}{n}}<\ln(n)+\ln \ln(n).}$

Sei ${\displaystyle \pi _{q,a}(x)}$ die Anzahl der Primzahlen kleiner gleich ${\displaystyle x}$ in der arithmetischen Progression ${\displaystyle a,a+q,a+2q,\cdots }$, wobei ${\displaystyle a,q}$ koprim sind (${\displaystyle (a,q)=1}$). Peter Gustav Lejeune Dirichlet (siehe Dirichletscher Primzahlsatz) und Adrien-Marie Legendre vermuteten, dass asymptotisch

${\displaystyle \pi _{q,a}(x)\sim {\frac {1}{\varphi (q)}}\operatorname {Li} (x),}$

mit ${\displaystyle \varphi (q)}$ der Eulerschen Phi-Funktion (der Anzahl zu ${\displaystyle q}$ teilerfremden Zahlen kleiner als ${\displaystyle q}$). Das wurde von Charles-Jean de La Vallée Poussin bewiesen mit ähnlichen Methoden wie beim Beweis des Primzahlsatzes.

Als Beispiel kann man das auf die Verteilung der Primzahlen auf ihre Endziffern im Dezimalsystem anwenden (analog gilt das für jede Basis). Es kommen nur die Ziffern 1, 3, 7, 9 in Betracht (außer für die Primzahlen 5 und 2 selbst) und aus dem Primzahlsatz für arithmetische Progressionen folgt, dass die Primzahlen unter ihren Endziffern gleich verteilt sind. Es gibt allerdings einige Ungleichgewichte, die Gegenstand der Forschung sind. So gibt es numerisch meist mehr Primzahlen der Form ${\displaystyle p=3\mod 4}$ als ${\displaystyle p=1\mod 4}$ unterhalb einer bestimmten Grenze, obwohl die Primzahlen asymptotisch auf beide Klassen gleich verteilt sind (Chebyshev’s Bias,[34] auch Primzahl-Rennen, nach Pafnuti Lwowitsch Tschebyschow). Nach John Edensor Littlewood wechselt ${\displaystyle \pi _{4,3}(x)-\pi _{4,1}(x)}$ auch unendlich oft das Vorzeichen. Ähnliche Phänomene gibt es bei Betrachtung anderer Kongruenzen als solchen mod ${\displaystyle 4}$. Wie K. Soundararajan und Oliver 2016 fanden, gibt es auch Abweichungen der Gleichverteilung wenn man die Verteilung der Endziffern bei aufeinanderfolgenden Primzahlen betrachtet.

Genauer wurde die Verteilung in arithmetischen Progressionen durch Arnold Walfisz[35][36] untersucht im Satz von Siegel und Walfisz (er basiert auf einem Resultat von Carl Ludwig Siegel[37]). Der Satz liefert einen asymptotischen Fehlerterm ${\displaystyle O\left(x\exp \left(-{\frac {C_{N}}{2}}(\ln x)^{\frac {1}{2}}\right)\right),}$ für die obige Formel. Dabei ist ${\displaystyle C_{N}}$ eine Konstante und ${\displaystyle N}$ eine beliebige Zahl mit ${\displaystyle q\leq {(\ln x)}^{N}}$.

Ursprünglich ist der Satz von Siegel und Walfisz für die Funktion

${\displaystyle \psi (x;q,a)=\sum _{n\leq x \atop n\equiv a{\pmod {q}}}\Lambda (n),}$

formuliert mit der Mangoldt-Funktion ${\displaystyle \Lambda (n)}$. Mit den bereits eingeführten Bezeichnungen (sowie wie oben ${\displaystyle (a,q)=1}$, ${\displaystyle q\leq (\ln x)^{N}}$) besagt der Satz dann, dass es für jedes N eine Konstante ${\displaystyle C_{N}}$ gibt, so dass:

${\displaystyle \psi (x;q,a)={\frac {x}{\varphi (q)}}+O\left(x\exp \left(-C_{N}(\ln x)^{\frac {1}{2}}\right)\right)}$

Der Satz ist nicht effektiv, da nichts über die Größe der Konstante ${\displaystyle C_{N}}$ ausgesagt wird. Schärfere Aussagen zum Fehlerterm im Dirichletschen Primzahlsatz für arithmetische Progressionen gibt der Satz von Bombieri und Winogradow (und die Vermutung von Elliott und Halberstam).

• E. Freitag, R. Busam: Funktionentheorie. 3. Auflage. Springer-Verlag, Berlin 2000. ISBN 3-540-67641-4.
• G. H. Hardy, E. M. Wright: An Introduction to the Theory of Numbers. 5. Auflage, Oxford University Press, Oxford 1979. ISBN 0-19-853171-0.
• Peter Bundschuh: Einführung in die Zahlentheorie. Springer 2008 (mit Beweis von Newman)

Wikibooks: Beweis des Primzahlsatzes nach Newman – Lern- und Lehrmaterialien

• PrimePages: How many primes are there? (englisch)
• Eric W. Weisstein: Prime Number Theorem. In: MathWorld (englisch).

1. Donald J. Newman: Analytic Number Theory. Springer, 1998. Newman: Simple Analytic Proof of the Prime Number Theorem. In: American Mathematical Monthly, Band 87, 1980, S. 693–696
2. Zu Newmans Beweis auch: J. Korevaar: On Newman’s quick way to the prime number theorem. In: Mathematical Intelligencer, Band 4, 1982, Nr. 3. Don Zagier: Newman’s Short Proof of the Prime Number Theorem. In: American Mathematical Monthly, Band 104, 1997, S. 705–708. Der Beweis ist auch dargestellt in Bundschuh: Einführung in die Zahlentheorie. Springer, 2008. Newman: Analytic Number Theory. Springer, 1998.
3. Arnold Walfisz: Weylsche Exponentialsummen in der neueren Zahlentheorie. VEB Deutscher Verlag der Wissenschaften 1963, S. 187. Der Beweis bei Walfisz stammt von Hans-Egon Richert. Derbyshire, Prime Obsession, Joseph Henry Press 2003, S. 244, bezeichnet das als die beste ihm bekannte Abschätzung des Fehlerterms.
4. L. Schoenfeld, Sharper Bounds for the Chebyshev Functions θ(x) and ψ(x). II, Mathematics of Computation, Band 30, 1976, S. 337–360
5. Dieser hatte sich 1792 oder 1793 mit dem Thema beschäftigt, siehe den Brief aus dem Jahr 1849 an Johann Franz Encke, Textarchiv – Internet Archive. Dort diskutiert er auch die Konstante von Legendre und den Integrallogarithmus.
6. Adrien-Marie Legendre: D’une loi très-remarquable observée dans l’énumération des nombres premiers. In: Théorie des nombres. 3. Auflage. Didot, Paris 1830, Band 2, S. 65–70, Textarchiv – Internet Archive
7. Pafnuti Lwowitsch Tschebyschew: Sur la fonction qui détermine la totalité des nombres premiers inférieurs à une limite donnée. In: Mémoires présentés à l’Académie Impériale des sciences de St.-Pétersbourg par divers savants, 6, 1851, S. 141–157. Auch in: Journal de mathématiques pures et appliquées, 1. F., 17, 1852, S. 341–365. Nachdruck in Andrej Andrejewitsch Markoff, Nikolai Jakowlewitsch Sonin (Hrsg.): Œuvres de P. L. Tchebychef. Band 1. Akademie, St. Petersburg 1898, S. 27–48, Textarchiv – Internet Archive.
8. Einen deutlich vereinfachten Beweis für eine schwächere Abschätzung gibt Don Zagier, Die ersten 50 Millionen Primzahlen, Elemente der Mathematik (Beihefte zur Zeitschrift), Band 15 (1977), S. 15 f., doi:10.5169/seals-10209 (frei zugänglich)
9. James Joseph Sylvester: On arithmetical series. In: Messenger of Mathematics, 21, 1892, S. 1–19, 87–120. Nachdruck in Henry Frederick Baker (Hrsg.): The Collected Mathematical Papers of James Joseph Sylvester. 4 Bände. University Press, Cambridge 1904–1912, Band 4. 1912, S. 687–731, archive.org.
10. Bernhard Riemann: Über die Anzahl der Primzahlen unter einer gegebenen Größe. In: Monatsberichte der Königlichen Preußischen Akademie der Wissenschaften zu Berlin, 1859, S. 671–680. Vgl. auch Wilhelm Scheibner: Ueber die Anzahl der Primzahlen unter einer beliebigen Grenze. In: Archiv der Mathematik und Physik, 5, 1860, S. 233–252.
11. Hans von Mangoldt: Zu Riemanns Abhandlung „Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse“. In: Journal für die reine und angewandte Mathematik, 114, 1895, S. 255–305.
12. Jacques Hadamard: Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques. (PDF; 1,3 MB). In: Bulletin de la Société Mathématique de France, 24, 1896, S. 199–220.
13. Charles de La Vallée Poussin: Recherches analytiques de la théorie des nombres premiers. In: Annales de la Société Scientifique de Bruxelles 20 B (1896), S. 183–256, 281–352, 363–397; 21 B (1897), S. 351–368.
14. Kürzere Versionen der Beweise von Hadamard, De la Vallée-Poussin sind in E. C. Titchmarsh: The Theory of the Riemann Zeta-Function. Clarendon Press, 1951, 1986, Kapitel 3
15. Atle Selberg: An elementary proof of the prime-number theorem. In: Annals of Mathematics, 50, 1949, Nr. 2, S. 305–313.
16. Paul Erdős: On a new method in elementary number theory which leads to an elementary proof of the prime number theorem. (PDF; 687 kB). In: Proceedings of the National Academy of Sciences of the United States of America, 35, 1949, S. 374–384.
17. Der elementare Beweis nach Erdös und Selberg wird in modifizierter Form auch in Hardy, Wright, Introduction to the theory of numbers, Oxford 1975, präsentiert
18. Die Werte für π(x) sind aus Chris K. Caldwell: How Many Primes Are There? Prime Pages, abgerufen am 12. Dezember 2015 (englisch).
19. Der Wert für π(10²⁶) ist aus D. B. Staple: The combinatorial algorithm for computing pi(x). Dalhousie University, abgerufen am 12. Dezember 2015 (englisch).
20. Der Wert für π(10²⁷) ist von Kim Walisch: New confirmed pi(10^27),… pi(10^29) prime counting function records. In: mersenneforum.org. Abgerufen am 1. Dezember 2016 (englisch).
21. John E. Littlewood: Sur la distribution des nombres premiers. In: Comptes Rendus de l'Académie des Sciences 158 (1914), S. 1869–1872.
22. Stanley Skewes: On the difference ${\displaystyle \pi (x)-\operatorname {Li} (x)}$. In: Journal of the London Mathematical Society 8 (1933), S. 277–283; On the difference ${\displaystyle \pi (x)-\operatorname {Li} (x)}$ (II). In: Proceedings of the London Mathematical Society 5 (1955), S. 48–70.
23. Russell Sherman Lehman: On the difference π(x) − li(x). (PDF; 2,6 MB). In: Acta Arithmetica 11 (1966), S. 397–410.
24. Herman J. J. te Riele: On the Sign of the Difference π(x) − li(x). (PDF; 550 kB). In: Mathematics of Computation, 48, 1987, S. 323–328. Vgl. Chris K. Caldwell: How many primes are there? (Memento vom 15. Oktober 2012 im Internet Archive) Kap. 3, History of the Prime Number Theorem.
25. Carter Bays, Richard H. Hudson: A new bound for the smallest x with π(x) > li(x). (PDF; 422 kB). In: Mathematics of Computation, 69, 2000, Nr. 231, S. 1285–1296.
26. E.C. Titchmarsh: The Theory of Functions, 2nd ed. Oxford University Press, 1960 (englisch).
27. Siehe Riemannsche Vermutung oder Riemann Prime Counting Function, Mathworld
28. Hans Riesel, Gunnar Göhl: Some calculations related to Riemann’s prime number formula. In: Mathematics of Computation. 24. Jahrgang, Nr. 112. American Mathematical Society, 1970, ISSN 0025-5718, S. 969–983, doi:10.2307/2004630 (englisch).
29. Eric W. Weisstein: Riemann Prime Counting Function. In: MathWorld (englisch).
30. Eric W. Weisstein: Gram Series. In: MathWorld (englisch).
31. The encoding of the prime distribution by the zeta zeros. Matthew Watkins, archiviert vom Original am 4. Februar 2013; abgerufen am 14. September 2008 (englisch).
32. Values of π(x) and Δ(x) for various values of x. Andrey V. Kulsha, abgerufen am 14. September 2008 (englisch).
33. Pierre Dusart: The ${\displaystyle k^{\rm {th}}}$ prime is greater than ${\displaystyle k(\ln k+\ln \ln k-1)}$ for ${\displaystyle k\geq 2}$. In: Mathematics of Computation. 68. Jahrgang, Nr. 225, 1999, S. 411–415, doi:10.1090/S0025-5718-99-01037-6 (englisch).
34. Chebyshev’s Bias, mathworld
35. A. Walfisz: Zur additiven Zahlentheorie II. Mathematische Zeitschrift, Band 40, 1936, S. 592–607
36. Zum Satz von Siegel-Walfisz siehe auch Harold Davenport: Multiplicative Number Theory. 2. Auflage. Springer, 1980, S. 133, Terry Tao, Notes Complex Analytic Multiplicative Number Theory (exercise 64)
37. Siegel: Über die Classenzahl quadratischer Zahlkörper. In: Acta Arithmetica, Band 1, 1935, S. 83–86