Potenzgerade
Unter der Potenzgeraden (Potenzlinie, Chordale) zweier Kreise versteht man den geometrischen Ort (die Menge) aller Punkte, deren Potenz in Bezug auf die beiden Kreise übereinstimmt. Sind die Kreise durch ihre Mittelpunkte und sowie ihre Radien und gegeben, so sind die Potenzen eines Punktes bezgl. der beiden Kreise
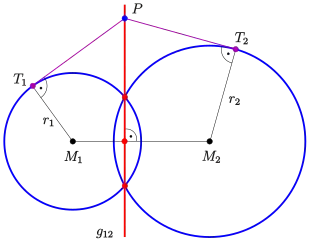
Liegen kollinear, so ist der Mittelpunkt von .
Ein Punkt gehört zur Potenzgerade , wenn
- gilt.
Die Potenzgerade ist nur definiert, wenn die gegebenen Kreise nicht konzentrisch sind, also keinen übereinstimmenden Mittelpunkt haben. Sind beide Radien gleich oder sogar 0, so ist die Potenzgerade die Mittelsenkrechte der Punkte .
Potenzgeraden spielen bei Kreisbüscheln eine wichtige Rolle: Ein Kreisbüschel ist eine Schar von Kreisen mit einer gemeinsamen Potenzgerade.[1]
Bezeichnungen:
J. Steiner nannte die Potenzgerade Linie der gleichen Potenzen.[2]
J.V. Poncelet verwandte chorde ideale.[3]
J. Plücker führte die Bezeichnung Chordale ein.[4]
M. Chasles bezeichnet sie als axe radical, was auch im Englischen (radical axis) üblich ist.[5]
O. Hesse nennt die Potenzgerade gemeinschaftliche Sekante, auch in dem Fall, dass die beiden Kreise keine (reellen) Punkte gemeinsam haben.[6]
Eigenschaften
Geometrische Form und Lage
Im Folgenden sind die Ortsvektoren der Punkte . Die definierende Gleichung der Potenzgerade lässt sich damit schreiben:
Aus der rechten Gleichung erkennt man
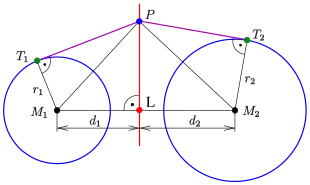
- Die als Potenzgerade definierte Punktmenge ist tatsächlich eine Gerade und steht senkrecht auf der Verbindungsgerade der Mittelpunkte. ( ist eine Normale der Potenzgerade!)
Dividiert man die Gleichung durch , erhält man die Hessesche Normalenform. Einsetzen der Mittelpunkte liefert die Abstände der Potenzgerade zu den Mittelpunkten:
- .
- Dabei ist .
(Bei Verwendung der äquivalenten linken Gleichung in der Form wird die Berechnung von besonders einfach.)
Schneiden sich die beiden Kreise, so geht die Potenzgerade durch die gemeinsamen Punkte. Falls sie sich nur berühren ist die gemeinsame Tangente die Potenzgerade.

Spezielle Lagen
- Für zwei sich schneidende Kreise (Fall 3) geht die Potenzgerade durch die beiden Schnittpunkte. Falls sich die beiden Kreise berühren (Fall 2 und Fall 4), stimmt die Potenzgerade mit der gemeinsamen Tangente überein.
Orthogonalkreise
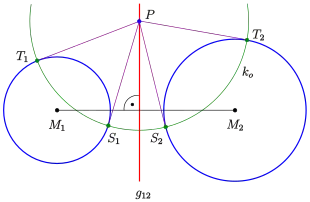
- Für die Punkte der Potenzgeraden, die außerhalb der gegebenen Kreise liegen, sind die Tangentenabschnitte an beide Kreise gleich lang (siehe den Artikel über Potenz). Sind die Berührpunkte der Tangenten durch an die beiden Kreise, so liegen auf einem die Kreise senkrecht schneidenden Kreis .
- Die Potenzgerade zweier Kreise ist die Menge der Mittelpunkte aller Kreise, welche die gegebenen Kreise rechtwinklig schneiden.
System orthogonaler Kreise
Die im vorigen Abschnitt enthaltene Möglichkeit zu zwei Kreisen ein System von Kreisen zu konstruieren, die die gegebenen Kreise orthogonal schneiden, lässt sich zu einer Konstruktion von zwei Systemen von Kreisen, die sich orthogonal schneiden[7][8], ausbauen:
Es seien zwei getrennt liegende Kreise (wie im vorigen Abschnitt), deren Mittelpunkte und Radien und deren Potenzgerade. Es werden nun diejenigen Kreise gesucht, deren Mittelpunkte auf der Gerade liegen und deren Potenzgerade zusammen mit auch ist. Es sei ein solcher Kreis, dessen Mittelpunkt von den Abstand und den Radius hat. Nach dem Resultat des vorigen Abschnitts ist dann
- , wobei fest sind.
Mit lässt sich diese Gleichung umformen zu:
- .

Gibt man den Radius vor, ergibt sich aus dieser Gleichung der Abstand des neuen Mittelpunktes von der (festen) Potenzgerade. In der Abbildung sind die neuen Kreise lila. Die grünen Kreise (siehe Abbildung) mit Mittelpunkte auf der Potenzgerade schneiden senkrecht und damit auch alle neuen Kreise (lila). Wenn man die (rote) Potenzgerade als y-Achse und als x-Achse wählt, haben die beiden Kreisscharen die folgenden Gleichungen:
- lila:
- grün:
( ist der Mittelpunkt eines grünen Kreises.)
Eigenschaften:
a) Die grünen Kreise schneiden sich alle auf der x-Achse in den beiden Punkten , den Polen des orthogonalen Kreissystems, d. h. die x-Achse ist die Potenzgerade der grünen Kreise.
b) Die lila Kreise haben keine (reellen) Punkte gemeinsam. Fasst man aber die reelle Ebene als Teil der komplexen Ebene auf, so schneiden sich die lila Kreise auf der y-Achse (gemeinsame Potenzgerade) in den beiden Punkten .

Sonderfälle:
a) Im Fall berühren sich sowohl die grünen als auch die lila Kreise im Nullpunkt. Sie bilden zwei sich orthogonal schneidende parabolische Kreisbüschel (siehe unten).
b) Lässt man auf den Punkt schrumpfen, d. h. , so vereinfachen sich die Gleichungen und es ist .

Zusammenfassung:
a) Für jede reelle Zahl gilt für die Kreisschar
- Je zwei Kreise haben die y-Achse als Potenzgerade.
- Für schneiden sich in den Punkten .
- Für haben keinen Punkt gemeinsam.
- Für berühren sich in dem Punkt .
b) Für jede reelle Zahl bilden die beiden Kreisscharen
- ein System orthogonaler Kreise. D.h.: schneiden sich für alle orthogonal.
- Für sind die Pole.
- Für sind die Pole.
- Für ist und das System ist parabolisch.
c) Die Gleichungen in b) lassen sich zur koordinatenfreien Formulierung verwenden:

- Sind die beiden Punkte gegeben, ihr Mittelpunkt und ihre Mittelsenkrechte, so beschreiben die beiden Gleichungen
- mit auf , aber nicht zwischen , und auf
- das durch eindeutig bestimmte orthogonale System von Kreisen. sind die Pole des Systems.
- Für muss man zusätzlich die beiden Potenzgeraden, die Achsen des Systems, vorgeben. Es ergibt sich das parabolische System:
- mit auf und auf .
Konstruktion mit Zirkel und Lineal:

Ein orthogonales Kreissystem ist durch die Vorgabe seiner Pole eindeutig bestimmt:
- Die Achsen (Potenzgeraden) sind die Gerade und die Mittelsenkrechte der Pole.
- Die Kreise (im Bild grün) durch haben ihre Mittelpunkte auf . Zu einem Punkt ist der Radius .
- Um einen Kreis der zweiten Schar (im Bild blau) mit Mittelpunkt auf zu zeichnen, bestimmt man mit dem Satz des Pythagoras den Radius aus wie in dem Bild gezeigt.
Falls ist, müssen die Achsen vorgegeben werden. Das System ist dann parabolisch und leicht zu zeichnen.
Kreisbüschel
Definition und Eigenschaften:
Sind zwei Kreise und ihre Potenzfunktionen, so ist für jedes
die Gleichung eines Kreises (siehe unten). Diese Schar von Kreisen nennt man das von erzeugte Kreisbüschel.
Die Potenzfunktion von ist
- .
Man rechnet leicht nach, dass gilt:
- haben dieselbe Potenzgerade wie .
(H): Schneiden sich in zwei Punkten , so gehen auch alle Kreise durch und die Gerade ist ihre gemeinsame Potenzgerade. Ein solches Kreisbüschel heißt elliptisch.
(P): Berühren sich in , so berühren sich alle und die gemeinsame Tangente ist die Potenzgerade. Das Kreisbüschel heißt parabolisch.
(E): Haben keinen Punkt gemeinsam, so auch alle Kreise und das Büschel heißt hyperbolisch.
Konkret:
Führt man so Koordinaten ein, dass
- ,
so ist die y-Achse ihre Potenzgerade (siehe oben).
Falls ist, haben die beiden Punkte
gemeinsam und das Kreisbüschel ist elliptisch.
Falls ist, haben den Punkt
gemeinsam und das Büschel ist parabolisch.
Falls ist, haben keinen Punkt gemeinsam und das Büschel ist hyperbolisch.
Die Berechnung der Potenzfunktion liefert die Gleichung des Kreises:
Quadratische Ergänzung und die Substitution (x-Koordinate des Mittelpunktes) führt auf die Mittelpunktsform
- .
Alternative Formen:
1) In der definierenden Gleichung des Kreisbüschels müssen nicht die Potenzfunktionen selbst stehen. Es können auch jeweils Vielfache davon verwendet werden.
2) Die Gleichung eines der beiden Kreise kann man auch durch die Gleichung der gewünschten Potenzgerade ersetzen. Die Potenzgerade kann man also als einen Kreis mit unendlich großem Radius ansehen. Z.B.:
- ,
beschreibt alle Kreise, die mit dem ersten Kreis die Gerade als Potenzgerade besitzen.
3) Um beide Kreise in der Definitionsgleichung formal gleich zu behandeln, verwendet man auch gelegentlich die symmetrisierte Form
- ,
wobei nicht gleichzeitig Null sein dürfen. Der Nachteil dieser Form: Sie ist bezgl. nicht eindeutig.
Anwendung:
a) Kreisspiegelungen und Möbiustransformationen sind kreistreue und winkeltreue Abbildungen der Ebene. Orthogonale Kreisbüschel spielen deshalb bei Untersuchungen dieser Abbildungen eine besondere Rolle.[9][10]
b) In der Elektrodynamik treten Kreisbüschel als Feldlinien auf. Sie werden dort, wie im Englischen (coaxal circles), auch koaxiale Kreise genannt.[11]
Radikal dreier Kreise, Konstruktion der Potenzgerade
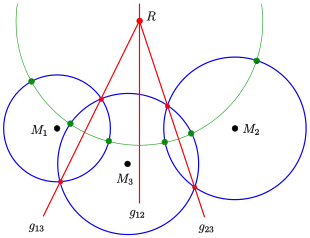
Der grüne Kreis schneidet die drei Kreise senkrecht.
- Sind drei Kreise gegeben, unter denen keine zwei konzentrisch sind, so existieren drei Potenzgeraden (jeweils eine zu zwei Kreisen). Falls die Mittelpunkte der gegebenen Kreise nicht auf einer Geraden liegen, schneiden sich die Potenzgeraden in einem Punkt (engl. radical center), und zwar im Mittelpunkt des Kreises, der die gegebenen Kreise rechtwinklig schneidet (engl. radical circle). Zum Nachweis: die Potenzgerade enthält alle Punkte, die vom i-ten und k-ten Kreis denselben tangentialen Abstand haben. Der Schnittpunkt von und muss also zu allen drei Kreisen denselben tangentialen Abstand besitzen und damit auch auf liegen.
- Diese Eigenschaft gibt die Möglichkeit die Potenzgerade von zwei sich nicht schneidenden Kreisen zeichnerisch zu bestimmen: Man zeichne einen dritten Kreis , der die gegebenen Kreise schneidet. Damit lassen sich die Potenzgeraden zeichnen. Ihr Schnittpunkt liegt auf , die als Lotgerade von auf die Gerade gezeichnet werden kann.
Weitere Konstruktion:
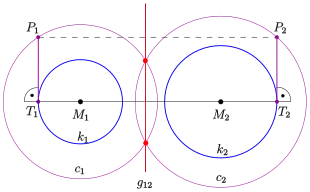
Es ist .
Die Punkte, die bezgl. eines Kreises die gleiche Potenz besitzen, liegen auf einem zu konzentrischen Kreis. Diese Eigenschaft lässt sich zu einer weiteren Methode zur Konstruktion der Potenzgerade zweier Kreise verwenden:
Sind zwei sich nicht schneidende Kreise gegeben, so lassen sich, wie in der Zeichnung gezeigt, zu jedem Kreis ein weiterer Kreis zeichnen, mit der Eigenschaft: Die Punkte der Kreise haben bezüglich der Kreise die gleiche Potenz. Formal: . Ist die Potenz groß genug gewählt, schneiden sich und liefern zwei Punkte der gesuchten Potenzgerade der Kreise .
Falls die Radien der beiden Kreise Null sind, ist die Potenzgerade die Mittelsenkrechte von und die Konstruktion ist die für Mittelsenkrechte übliche.
Literatur
- G. Aumann: Kreisgeometrie, S. 45
- Jakob Steiner: Einige geometrische Betrachtungen. In: Journal für die reine und angewandte Mathematik, Band 1, 1826, S. 165
- Ph. Fischer: Lehrbuch der analytische Geometrie, Darmstadt 1851, Verlag Ernst Kern, p. 67
- H. Schwarz: Die Elemente der analytischen Geometrie der Ebene, Verlag H. W. Schmidt, Halle, 1858, S. 218
- Michel Chasles, C. H. Schnuse: Die Grundlehren der neuern Geometrie, erster Theil, Verlag Leibrock, Braunschweig, 1856, S. 312
- O. Hesse: Analytische Geometrie der geraden Linie, des Punktes und des Kreises in der Ebene, Teubner-Verlag, Leipzig, 1881, S. 195.
- A. Schoenflies, R. Courant: Einführung in die Analytische Geometrie der Ebene und des Raumes, Springer-Verlag, 1931, S. 113
- C. Caratheodory: Funktionentheorie, Birkhäuser-Verlag, Basel, 1961, ISBN 978-3-7643-0064-7, S. 46
- Caratheodory: Funktionentheorie, S, 47.
- R. Sauer: Ingenieur-Mathematik: Zweiter Band: Differentialgleichungen und Funktionentheorie, Springer-Verlag, 1962, ISBN 978-3-642-53232-0, S. 105
- Clemens Schaefer: Elektrodynamik und Optik, Verlag: De Gruyter, 1950, ISBN 978-3-11-230936-0, S. 358.
- Günter Aumann: Kreisgeometrie, Springer Spektrum, 2015, ISBN 978-3-662-45305-6, S. 39
- Max Koecher, Aloys Krieg: Ebene Geometrie. Springer, 2013, ISBN 978-3-662-06809-0, S. 138–140
- Harald Scheid, Wolfgang Schwarz: Elemente der Geometrie. Springer, 2016, ISBN 978-3-662-50323-2, S. 156–158
Weblinks
- Eric W. Weisstein: Radical line. In: MathWorld (englisch).
- Geogebra: Potenzgeraden interaktiv