Peanosche Fläche

In der Mathematik ist die peanosche Fläche der Graph der Funktion

f(x,y)=(2x^{2}-y)(y-x^{2})\ .

Modell der peanoschen Fläche in der Dresdener Modellsammlung[1]

Sie wurde 1899 von Giuseppe Peano als Gegenbeispiel zu einer Vermutung für die Existenz eines lokalen Maximums/Minimums einer Funktion von zwei Variablen angegeben.[2][3][4]

Diese Fläche wurde 1920 von Georg Scheffers in seinem Lehrbuch der darstellenden Geometrie[5] als Fläche von Peano bezeichnet. Sie wird auch Peano-Sattel genannt.[6][7]

Die zu widerlegende Vermutung

Vermutung: Haben die Schnitte des Graphen einer Funktion $f(x,y)$ mit Ebenen durch die $z$ -Achse an der Stelle $(0,0)$ alle ein lokales Maximum, so hat auch die Funktion $f$ an der Stelle $(0,0)$ ein lokales Maximum.

Die Fläche von Peano zeigt: Diese Vermutung ist falsch. Dafür genügt es zu zeigen, dass für die Funktion $f(x,y)=(2x^{2}-y)(y-x^{2})$ gilt:

Jede Schnittkurve der Fläche mit einer Ebene durch die $z$ -Achse besitzt im Punkt $(0,0,0)$ ein lokales Maximum.
In jeder Umgebung von $(0,0)$ besitzt $f$ sowohl positive als auch negative Werte.

Peano-Fläche

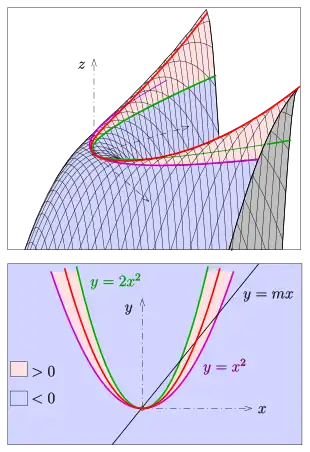
Eigenschaften der Funktion f

Die Funktion $f(x,y)=(2x^{2}-y)(y-x^{2})$ besitzt folgende Eigenschaften:

$f(x,y)=0\;$ auf den Parabeln $y=2x^{2}$ und $y=x^{2}$ .
$f(x,y)>0\;$ zwischen diesen Parabeln, also für $x^{2}<y<2x^{2}$ (im Bild rosa) und
$f(x,y)<0\;$ sonst (im Bild hellblau).
Schränkt man $f$ durch $ax+by=0$ mit $a^{2}+b^{2}>0$ ein, so prüft man leicht nach, dass jede solche Einschränkung von $f$ im Nullpunkt $(0,0,0)$ ein lokales Maximum besitzt.
Die Funktionswerte entlang der Parabel $y={\sqrt {2}}x^{2}$ (im Bild rot) sind außerhalb des Nullpunktes positiv (!). $f$ hat also im Nullpunkt einen Sattelpunkt. (Für diese Überlegung kann man eine beliebige zwischen den Parabeln verlaufende Kurve verwenden.)

Der übliche Sattelpunkt-Test mit der Determinante der Hessematrix liefert kein Ergebnis, da die Determinante 0 ist.[8]

Weblinks: weitere Modelle der peanoschen Fläche

Literatur

Peanosche Fläche. In: math.tu-dresden.de. Abgerufen am 2. August 2020.
Arnold Emch: A model for the Peano Surface. In: American Mathematical Monthly. 29, Nr. 10, 1922, S. 388–391.
Angelo Genocchi, Giuseppe Peano (Hrsg.): Differentialrechnung und Grundzüge der Integralrechnung. B.G. Teubner, 1899, S. 332.
Kuno Fladt: Analytische Geometrie spezieller Flächen und Raumkurven, Springer-Verlag, 2013, S. 197.
Georg Scheffers: Lehrbuch der darstellenden Geometrie. Band II, 1920, S. 261–263.
S. N. Krivoshapko, V. N. Ivanov: Encyclopedia of Analytical Surfaces. Springer, 2015. Siehe insbesondere den Abschnitt Peano Saddle, S. 562–563.
George K. Francis: A Topological Picturebook. Springer-Verlag, New York 1987, ISBN 0-387-96426-6, S. 88.
Kurt Meyberg, Peter Vachenauer: Höhere Mathematik 1. Springer-Verlag, 1995, ISBN 3-540-59188-5, S. 403.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Peanosche Fläche. In: math.tu-dresden.de. Abgerufen am 2. August 2020.

[2] Arnold Emch: A model for the Peano Surface. In: American Mathematical Monthly. 29, Nr. 10, 1922, S. 388–391.

[3] Angelo Genocchi, Giuseppe Peano (Hrsg.): Differentialrechnung und Grundzüge der Integralrechnung. B.G. Teubner, 1899, S. 332.

[4] Kuno Fladt: Analytische Geometrie spezieller Flächen und Raumkurven, Springer-Verlag, 2013, S. 197.

[5] Georg Scheffers: Lehrbuch der darstellenden Geometrie. Band II, 1920, S. 261–263.

[6] S. N. Krivoshapko, V. N. Ivanov: Encyclopedia of Analytical Surfaces. Springer, 2015. Siehe insbesondere den Abschnitt Peano Saddle, S. 562–563.

[7] George K. Francis: A Topological Picturebook. Springer-Verlag, New York 1987, ISBN 0-387-96426-6, S. 88.

[8] Kurt Meyberg, Peter Vachenauer: Höhere Mathematik 1. Springer-Verlag, 1995, ISBN 3-540-59188-5, S. 403.