Ovoid (Projektive Geometrie)

Ein Ovoid ist in der projektiven Geometrie eine kugelähnliche Punktmenge (Fläche) in einem projektiven Raum der Dimension $n\geq 3$ . Ein Ovoid ist das räumliche Analogon zu einem Oval in einer projektiven Ebene. Die einfachsten Beispiele in reellen projektiven Räumen sind Hyperkugeln (Quadriken).

Zur Definition eines Ovoids:
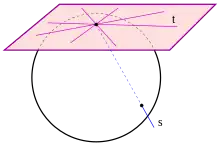
t Tangente, s Sekante

Die wesentlichen geometrischen Eigenschaften eines Ovoids ${\mathcal {O}}$ sind:

1) Eine Gerade trifft ${\mathcal {O}}$ in höchstens 2 Punkten,

2) die Tangenten in einem Punkt überdecken eine Hyperebene (und nicht mehr),

3) ${\mathcal {O}}$ enthält keine Geraden.

Eigenschaft 2) schließt ausgeartete Fälle (Kegel, …) aus. Eigenschaft 3) schließt Regelflächen (z. B. einschalige Hyperboloide) aus.

Auf der einen Seite macht die Tatsache, dass es keine nicht-desarguesschen projektiven Räume gibt, die Diskussion gegenüber dem ebenen Fall (es gibt nicht-desarguessche Ebenen) einfacher, andererseits gibt es nicht in jedem pappusschen Raum (projektiver Raum über einem Körper) eine Quadrik, die ein Ovoid ist. (In jeder pappusschen Ebene aber gibt es ovale Kegelschnitte!)

Ein Ovoid ist aufgrund der Definition eine spezielle quadratische Menge.

Ovoide spielen bei der Konstruktion von Möbius-Ebenen bzw. Möbius-Räumen eine wesentliche Rolle.

Definition eines Ovoids

Eine Menge ${\mathcal {O}}$ von Punkten in einem projektiven Raum der Dimension $\geq 3$ heißt Ovoid, wenn gilt:

(1) Eine beliebige Gerade

g

trifft

{\mathcal {O}}

in höchstens 2 Punkten.
Falls

|g\cap {\mathcal {O}}|=0

ist, heißt

g

Passante, falls

|g\cap {\mathcal {O}}|=1

ist, heißt

g

Tangente und falls

|g\cap {\mathcal {O}}|=2

ist, heißt

g

Sekante.

(2) Für jeden Punkt

P\in {\mathcal {O}}

gilt: Die Tangenten in

P

überdecken genau eine Hyperebene, die Tangential-Hyperebene, (projektiver Unterraum der Dimension

n-1

).

(3)

{\mathcal {O}}

enthält keine Geraden.

Ein Ovoid ist bezüglich der Hyperebenenschnitte eine homogene Struktur, denn es gilt

Ist ${\mathcal {O}}$ ein Ovoid und $\varepsilon$ eine Hyperebene, die wenigstens 2 Punkte von ${\mathcal {O}}$ enthält, so ist $\varepsilon \cap {\mathcal {O}}$ ein Ovoid (Oval, falls d=3) in der Hyperebene $\varepsilon$ .

Für endliche projektive Räume der Dimension $d\geq 3$ (d. h., Punktmenge und Geradenmenge sind endlich, der Raum ist über einem Körper koordinatisierbar[1]) gilt:

Ist ${\mathcal {O}}$ ein Ovoid in einem endlichen projektiven Raum der Dimension $d\geq 3$ , so ist ${\color {red}d=3}$ .

(Es gibt also im endlichen Fall nur im 3-dimensionalen Raum Ovoide !)[2]

In einem projektiven Raum der Ordnung $n>2$ (d. h., jede Gerade enthält $n+1$ Punkte) und Dimension $d={\color {red}3}$ ist eine Menge von Punkten ${\mathcal {O}}$ genau dann ein Ovoid, wenn $|{\mathcal {O}}|=n^{2}+1$ ist und keine drei Punkte von ${\mathcal {O}}$ kollinear (auf einer Gerade) liegen.[3]

Ersetzt man in der Definition das Wort projektiv durch affin, so erhält man die Definition eines affinen Ovoids.

Gibt es zu einem (projektiven) Ovoid eine passante Hyperebene, so kann man diese als Fernhyperebene erklären und das Ovoid ist in dem zugehörigen affinen Raum ein affines Ovoid. Umgekehrt ist jedes affine Ovoid in dem projektiven Abschluss (Zufügen einer Fernhyperebene) ein (projektives) Ovoid.

Beispiele

Im reellen projektiven Raum (inhomogene Darstellung)

${\mathcal {O}}=\{(x_{1},...,x_{d})\in \mathbb {R} ^{d}\;|\;x_{1}^{2}+\cdots +x_{d}^{2}=1\}\ ,$ (Hyperkugel)
${\mathcal {O}}=\{(x_{1},...,x_{d})\in \mathbb {R} ^{d}\;|x_{d}=x_{1}^{2}+\cdots +x_{d-1}^{2}\;\}\;\cup \;\{{\text{Fernpunkt der }}x_{d}{\text{-Achse}}\}$

Die beiden Beispiele sind Quadriken und projektiv äquivalent. (Siehe hierzu auch die Beispiele in Oval.)

Wie bei Ovalen erhält man hier einfache Beispiele, die keine Quadriken sind:

(a) Man füge eine halbe Hyperkugel und ein halbes Hyperellipsoid glatt zusammen.

(b) Man ersetze in den ersten beiden Beispielen den Term

x_{1}^{2}

durch

x_{1}^{4}

.

Bemerkung: Die reellen Beispiele lassen sich nicht auf den komplexen Fall (Räume über $\mathbb {C}$ ) übertragen. In komplexen projektiven Räumen der Dimension $d\geq 3$ gibt es keine ovoidalen Quadriken. Im komplexen Fall liegen auf einer nichtausgearteten Quadrik immer Geraden.

Aber es gilt:

In jedem nicht-endlichen projektiven Raum lassen sich mit Hilfe transfiniter Induktion Ovoide nachweisen.[4]

Endliche Beispiele

Ist ${\mathcal {O}}$ ein Ovoid in einem endlichen projektiven Raum der Dimension $d=3$ über einem Körper $K$ der Charakteristik ${\color {red}\neq }2$ , so ist ${\mathcal {O}}$ eine Quadrik.[5]

Dass das letzte Resultat im geraden Fall falsch ist, zeigen die folgenden Beispiele:

Es sei $K=GF(2^{m}),\;m$ ungerade und $\sigma$ der Automorphismus $x\mapsto x^{(2^{\frac {m+1}{2}})}\;.$

Dann ist

{\mathcal {O}}=\{(x,y,z)\in K^{3}\;|\;z=xy+x^{2}x^{\sigma }+y^{\sigma }\}\;\cup \;\{{\text{Fernpunkt der }}z{\text{-Achse}}\}

ein Ovoid im 3-dimensionalen projektiven Raum über

K

(in inhomogenen Koordinaten).

{\mathcal {O}}

ist nur im Fall

m=1

eine Quadrik.[6]

{\mathcal {O}}

heißt Tits-Suzuki-Ovoid.

Wann ist ein Ovoid eine Quadrik?

Eine ovoidale Quadrik zeichnet sich durch besonders viele Symmetrien aus. Es gilt:

Es sei ${\mathcal {O}}$ ein Ovoid in einem projektiven Raum ${\mathfrak {P}}$ und $\varepsilon$ eine Hyperebene eines mindestens 2-dimensionalen desargueschen projektiven Raums (im 2-dim. Fall ist ${\mathcal {O}}$ ein Oval) der Charakteristik $\neq 2$ . Liegt das Ovoid symmetrisch zu jedem Punkt $P\in \varepsilon \setminus {\mathcal {O}}$ (d. h., es gibt eine involutorische Perspektivität mit Zentrum $P$ , die ${\mathcal {O}}$ invariant lässt), so ist ${\mathfrak {P}}$ pappussch und ${\mathcal {O}}$ eine Quadrik.[7]

Ein Ovoid ${\mathcal {O}}$ in einem pappusschen projektiven Raum ist eine Quadrik, wenn die Gruppe der ${\mathcal {O}}$ invariant lassenden Projektivitäten auf ${\mathcal {O}}$ 3-fach transitiv operiert, d. h., zu 2 Tripeln von Punkten $A_{1},A_{2},A_{3},\;B_{1},B_{2},B_{3}$ gibt es eine Projektivität $\pi$ mit $\pi (A_{i})=B_{i},\;i=1,2,3$ .[8]

Im endlichen Fall folgt aus dem Satz von Segre:

Es sei ${\mathcal {O}}$ ein Ovoid in einem endlichen desargueschen projektiven 3-dimensionalen Raum ${\mathfrak {P}}$ ungerader Ordnung. Dann ist ${\mathfrak {P}}$ pappussch und ${\mathcal {O}}$ eine Quadrik.

Verallgemeinerung: Halbovoid

Lässt man bei der Definition eines Ovoids die Bedingung (1) weg, so erhält man die Definition eines Halbovoids:

Eine Punktmenge

{\mathcal {O}}

eines projektiven Raums heißt Halbovoid (engl.: semi ovoid), wenn gilt:

(HO1) Für jeden Punkt

P\in {\mathcal {O}}

gilt: Die Tangenten (Geraden, die mit

{\mathcal {O}}

nur einen Punkt gemeinsam haben) in

P

überdecken genau eine Hyperebene.

(HO2)

{\mathcal {O}}

enthält keine Geraden.

Halb hat also hier keine mengenmäßige Bedeutung, sondern bedeutet schwächere Voraussetzungen.

Ein Halbovoid ist eine spezielle hermitesche Menge (engl.: semi quadratic set[9]), die eine Verallgemeinerung der quadratischen Menge ist. Die Eigenschaft, die eine hermitesche von einer quadratischen Menge unterscheidet, ist, dass eine Gerade mit einer hermiteschen Menge mehr als 2 Punkte gemeinsam haben kann ohne, dass sie ganz enthalten ist.

Beispiele von Halbovoiden sind isotrope Punktmengen von hermiteschen Formen, sog. hermitesche Quadriken.

Auch für Halbovoide findet man in der Literatur Kriterien, wann ein Halbovoid eine hermitesche Quadrik ist. (z. B.[10])

Halbovoide werden analog den ovoidalen Möbiusebenen, zur Konstruktion von Möbius-Geometrien verwendet.

Weblinks

E. Hartmann: Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes. Skript, TH Darmstadt (PDF; 891 kB), S. 121–123.

Siehe auch

Einzelnachweise

P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 28
P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 48
P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 48
W. Heise: Bericht über $\kappa$ -affine Geometrien, Journ. of Geometry 1 (1971), S. 197–224, Satz 3.4.
P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 49
P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 52
H. Mäurer: Ovoide mit Symmetrien an den Punkten einer Hyperebene, Abh. Math. Sem. Hamburg 45 (1976), S. 237–244
J. Tits: Ovoides à Translations, Rend. Mat. 21 (1962), S. 37–59.
F. Buekenhout: A Characterization of Semi Quadrics, Atti dei Convegni Lincei 17 (1976), S. 393–421.
K.J. Dienst: Kennzeichnung hermitescher Quadriken durch Spiegelungen, Beiträge zur geometrischen Algebra (1977), Birkhäuser-Verlag, S. 83–85.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 28

[2] P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 48

[3] P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 48

[4] W. Heise: Bericht über $\kappa$ -affine Geometrien, Journ. of Geometry 1 (1971), S. 197–224, Satz 3.4.

[5] P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 49

[6] P. Dembowski: Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8, S. 52

[7] H. Mäurer: Ovoide mit Symmetrien an den Punkten einer Hyperebene, Abh. Math. Sem. Hamburg 45 (1976), S. 237–244

[8] J. Tits: Ovoides à Translations, Rend. Mat. 21 (1962), S. 37–59.

[9] F. Buekenhout: A Characterization of Semi Quadrics, Atti dei Convegni Lincei 17 (1976), S. 393–421.

[10] K.J. Dienst: Kennzeichnung hermitescher Quadriken durch Spiegelungen, Beiträge zur geometrischen Algebra (1977), Birkhäuser-Verlag, S. 83–85.