Normalisierter Fluss
Ein flussbasiertes generatives Modell ist ein generatives Modell, welches die Wahrscheinlichkeitsdichte der zugrundeliegenden Trainingsdaten schätzt, indem der normalisierte Fluss (normalizing flow)[1] berechnet wird. Der normalizing flow wird aus den Rechenregeln zum Wechseln der Variablen bei Integration (siehe Transformationssatz) hergeleitet, wobei eine einfache Verteilung in die komplizierte Zielverteilung transformiert wird.
Hintergrund
Normalisierten Flüssen liegt die folgende Tatsache zugrunde: Betrachten wir die bijektive Abbildung , sodass , dann gilt laut Transformationssatz
wobei der Betrag der Funktionaldeterminante ist und durch neuronale Netze parametrisiert wird.
Methode
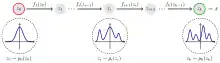
Log Likelihood
Betrachte Bijektionen , sodass , sodass .
Aufgrund des Transformationssatzes gilt:
- bzw.
daher gilt
und wiederholtes Einsetzen der Regel liefert:
Training
Ziel des Trainings ist es die Kullback-Leibler-Divergenz zwischen der geschätzten Wahrscheinlichkeitsdichte und der wahren, die Stichproben generierende, Wahrscheinlichkeitsdichte zu minimieren:
- .
Durch Schätzen des Erwartungswertes in der Kullback-Leibler-Divergenz mithilfe einer Realisierung des Stichprobenmittelwertes (und Vernachlässigung konstanter Terme) können die optimalen Maximum-Likelihood Parameter geschätzt werden:
Varianten
Planarer Fluss
Das früheste Beispiel einer Abbildung ist der planare Fluss[1]. Bei gegebener Aktivierungsfunktion , und Parametern mit entsprechender Dimension, ist
und die inverse (ohne allgemeingültige geschlossene Form).
Der Jacobian ist .
Damit der Fluss invertierbar ist, muss die Determinante überall ungleich null sein, was z. B. mit und der Fall ist.
Einzelnachweise
- Danilo Jimenez Rezende, Shakir Mohamed: Variational Inference with Normalizing Flows. 14. Juni 2016, arxiv:1505.05770 (englisch).