Nanoindentierung
Die Nanoindentierung (auch instrumentierter Eindringversuch) ist eine Methode der Werkstoffprüfung zur Bestimmung der Härte von Materialien auf kleinen Längenskalen (Nanometer, nm). Hauptanwendungsgebiet ist die Härtebestimmung an dünnen Schichten.
Geschichte
Die Untersuchung der Materialeigenschaften von Metallen ist bereits seit dem Mittelalter[2] von Interesse. Spätestens im Zuge der Industrialisierung ist es unerlässlich geworden, qualitativ hochwertige metallische Werkstoffe für die verschiedensten Aufgaben herstellen zu können. Um den immer weiter wachsenden Ansprüchen an die Werkstoffe genügen zu können, ist ein gutes Verständnis der Materialparameter, wie zum Beispiel Härte, Brüchigkeit und Rauheit, zwingend notwendig. All diese Materialeigenschaften wurden bereits früh mithilfe von sogenannten Indentationstests, bei denen zunächst nur der plastische Abdruck nach Aufschlagen eines Hammers vermessen wurde, untersucht. Konzeptionell entsprechen die heutigen Messverfahren zur Bestimmung der Härte noch immer der Vorgehensweise von Friedrich Mohs: Mittels Normmaterialien verschiedener Härte wird ein zu testendes Material plastisch verformt. Anhand der entstehenden plastischen Verformung wird dann die Härte in Relation zu den Normmaterialien festgelegt. Auf der Mohs’schen Skala von 1 (Talk) bis 10 (Diamant) haben die in der vorliegenden Arbeit verwendeten Materialien Kupfer und Aluminium eine Härte von 3 beziehungsweise 2.3...2.9.[3] Es stellt sich damals wie heute die Frage, wie bestimmte makroskopische Materialeigenschaften beeinflussbar sind. Oftmals schließen sich wünschenswerte Eigenschaften gegenseitig aus: So ist es zum Beispiel eine besondere Herausforderung, ein gleichzeitig hartes und duktiles Material zu finden. Heute können wir auf atomarer Ebene nach den Ursachen für die makroskopischen Materialeigenschaften suchen, und es stehen zunehmend mehr Möglichkeiten zur Verfügung, um auf kleinsten Längenskalen Materialien zu bearbeiten. Spätestens seit der richtungsweisenden Rede von Feynman[4] hat eine Miniaturisierung von Gebrauchsgegenständen (insbesondere elektrischen) eingesetzt. Das stellt natürlich ganz neue Anforderungen an die mechanischen Eigenschaften der Werkstoffe. Gleichzeitig ist die Auflösung der Messapparaturen deutlich gestiegen. War es 1968 noch bahnbrechend, Belastungstests auf der μm-Skala durchzuführen,[5] so sind heute Messungen auf der Å-Skala machbar.[6]
Methode
Die Nanoindentierung ist von der klassischen Härteprüfung abgeleitet, findet aber in viel kleinerem Maßstab statt. Es wird eine Diamantspitze mit bekannter Geometrie in die zu prüfende Oberfläche hineingedrückt. Durch die Miniaturisierung des Aufbaues ist es nur unter großem Aufwand möglich die Fläche des im Prüfling verbleibenden Härteeindruckes zu messen, wie das bei üblichen Verfahren zur Härtemessung getan wird.[7] Deshalb werden bei der Nanoindentierung während des Versuchs die aufgebrachte Eindringkraft und der Eindringweg der Spitze gleichzeitig gemessen. Durch die bekannte Geometrie der Prüfspitze und den Messdaten für Eindringkraft und Eindringweg kann die Kontaktfläche, und in weiterer Folge die Härte berechnet werden.
Der Messkopf für die Nanoindentierung (Hysitron Triboscope) besteht aus einem Dreiplattenkondensator und wird auf einem Rasterkraftmikroskop angebracht. Wird eine elektrische Spannung an den Kondensator angelegt, entsteht eine Kraft auf die mittlere Kondensatorplatte, die einen Stift mit einer Diamantspitze in die zu prüfende Oberfläche drückt. Die Verschiebung der mittleren Kondensatorplatte bewirkt eine Kapazitätsänderung des Kondensators und man erhält die erforderlichen Kraft- und Eindringtiefen Daten zur Ermittlung der Härte. Als Grenze zwischen Mikro- und Nanomessbereich sind nach DIN EN ISO 14577 0,2 µm festgelegt. Die meisten Geräte zur instrumentierten Eindringprüfung messen jedoch auch im Mikrobereich bis hin zur Grenze zum Makroprüfbereich von 2 N.
Warum Nanoindentation?
Zunächst ist es natürlich ganz allgemein ein Ziel, Materialeigenschaften mit immer höherer Auflösung zu vermessen – und so den relativen Fehler der Messungen zu minimieren. Je kleiner außerdem die untersuchten Proben sind, desto genauer lassen sie sich präparieren und desto kleiner sind daher die Fluktuationen aufgrund von Unreinheiten. Der Einfluss der einzelnen Parameter eines Materials kann also besser separiert werden. Während die Indentation auf der μm-Skala mittlerweile recht gut verstanden ist, sind bei der Nanoindentation (auf der nm-Skala) noch viele Fragen offen. Das heißt insbesondere, dass die atomistischen Prozesse und deren Rückwirkungen auf die makroskopischen Materialeigenschaften noch nicht im Detail verstanden sind.
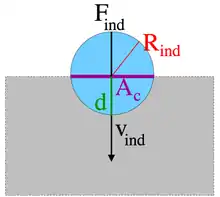
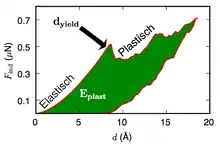
Nanoindentation in Metallen ist ein komplexer Prozess,[8][9] mit dem sowohl elastische als auch plastische Eigenschaften untersucht werden können. Wenn der Indenter in das Material hinein gedrückt wird, deformiert sich dieses zunächst elastisch. Unter weiterer Indentation bis hin zur kritischen Eindringtiefe dyield führt die entstehende Plastizität zunächst zu einem Lasteinbruch in der Kraft. Sobald die ersten Versetzungen erzeugt wurden, breiten sich diese aus, reagieren miteinander und es findet Materialtransport statt. Die meisten dieser atomistischen Prozesse haben direkte Konsequenzen für die Kraft , die auf den Indenter wirkt; der Indenter dringt also nicht mehr in ein ideales, sondern ein durch den Indentationsprozess gehärtetes Material ein (Workhardening).
Während ein idealer Kristall durch ein reines, ideales Kristallgitter charakterisiert wird, ist ein realer Kristall durchsetzt mit verschiedenen Arten von Gitterfehlern. Induziert das Kristallgitter eine Längenskala für das Substrat, so wird eine weitere Längenskala durch die Größe und Wechselwirkungsreichweite der Gitterfehler vorgegeben. Diese Längenskala ist inhärent größer als diejenige der Gitterkonstante. Weil aber weiter die makroskopischen Materialeigenschaften deutlich mit den mikroskopischen Gitterstrukturen variieren, sind reale Kristalle also durch eine Kopplung von verschiedenen Längenskalen dominiert. Es ist daher für ein Verständnis der makroskopischen Materialeigenschaften auch ein Verständnis der atomistischen Prozesse notwendig.
Die Methode der Nanoindentation ist besonders gut geeignet um den Zusammenhang zwischen mikroskopischen Materialparametern und makroskopischen Materialeigenschaften zu untersuchen. Während in einem klassischen Härtetest von makroskopischen Beobachtungen auf mikroskopische Eigenschaften geschlossen wird, verfolgen wir hier nun einen reziproken Ansatz, bei dem direkt die mikroskopischen Eigenschaften untersucht werden. Eine Untersuchung der atomistischen Struktur von Werkstoffen ermöglicht es, neue kontinuumstheoretische Modelle zu entwickeln.[10] So wurde zum Beispiel das Modell der geometrisch notwendigen Versetzungen aufgrund von Nanoindentation entwickelt.[11] Die Reaktion eines Materials auf die Belastung durch den Indenter kann sehr unterschiedlich sein. Am einfachsten zu verstehen ist der linear elastische Bereich – auch wenn dieser aufgrund der mehrachsigen Verspannung im Detail kompliziert zu beschreiben ist. Denn er ist nicht nur reversibel, sondern in ihm bleibt auch die Kristallstruktur erhalten. Im Hinblick auf seine Gitterstruktur bleibt ein idealer Kristall im elastischen Bereich homogen.
Komplizierter wird es, wenn sich die Kristallstruktur – also die Bindungen zwischen den Atomen unter der Belastung ändert, das Substrat also inhomogen wird. So wurden mittels der Nanoindentation Phänomene entdeckt, die bisher nicht durch die Kontinuumstheorie beschrieben wurden:[12] Es können zum Beispiel Phasentransformationen der Gitterstruktur auftreten, die zu (reversiblen) Lasteinbrüchen in der Kraft führen. Diese Lasteinbrüche rühren dann jedoch nicht von einsetzender Defektbildung her und sind damit in herkömmlichen kontinuumstheoretischen Modellen nicht enthalten.[13] Weiter können für andere Klassen von Materialien ganz andere Phänomene auftreten. So werden zum Beispiel im amorphen Silizium Scherbänder beobachtet.[14][15] Allgemein können Bindungsänderungen zu drastischen Effekten führen: So wurde kürzlich eine Kristallstruktur gefunden, die bei geringerer Dichte härter als Diamant ist.[16]
Obwohl die Methode der Indentation eigentlich direkt auf die freie Oberfläche wirkt, so beeinflusst dennoch das Geschehen innerhalb des Substrats die Reaktion des Materials auf die Belastung durch den Indenter erheblich. Der naheliegende Schluss, dass die gemessenen Eigenschaften durch die freie Oberfläche dominiert werden, ist trügerisch, denn der Indenter wirkt wie eine Lupe und fokussiert die maximale Scherspannung im Material.[17] Durch die lange Reichweite in den Wechselwirkungen der Verspannungen im Substrat können also mittels Indentation auch Rückschlüsse auf die Bulk-Eigenschaften gezogen werden. Das macht die Methode der Indentation auch für die Untersuchung von Einkristallen interessant. Während ein realer monodisperser Kristall in seinen Eigenschaften maßgeblich durch Versetzungen und Korngrenzen bestimmt ist, betrachten wir hier nur ideale einkristalline Materialien.
Indenterform
Die Form der Indenterspitze (Indenterform) ist üblicherweise entweder pyramidisch, rechteckig oder sphärisch. Sie beeinflusst stark die gewonnenen Resultate. Beispielsweise hinterlässt ein spitzer Indenter einen anderen plastischen Abdruck als ein sphärischer Indenter. Da in Abhängigkeit von der Indenterform die Verspannungen unter dem Indenter sehr verschieden sind, werden jeweils verschiedene Gleitsysteme aktiviert. Bei der Methode der Indentation gibt es daher eine starke Beeinflussung der ermittelten Kennwerte durch die Messmethode.[8] Es ist daher notwendig zu einem Messwert immer auch die verwendete Methode anzugeben.
Indentation als Härtetest
Die Methode der Härtemessung mittels Indentation ist prinzipiell recht einfach. Dabei wird der Indenter mit einer gewissen Kraft in ein Material eingedrückt und die wirkende Kraft gemessen. Dann kann der plastische Abdruck vermessen werden und daraus die Kontaktfläche approximiert werden. Über den Zusammenhang wird dann die Härte berechnet.
Materialeigenschaften auf der Nanoskala
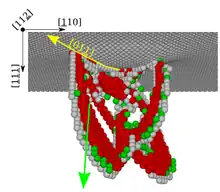
Durch atomistische Bewegungen können sich Materialeigenschaften drastisch ändern.[17] Dies motiviert die Herstellung und Untersuchung von sogenannten Nano-Materialien. Solche Materialien können härter als Diamant sein[18] oder ihre plastische Verformungen können ausheilen. Auf der anderen Seite sind für klassische Materialien die Ursachen ihrer Materialeigenschaften noch nicht umfassend verstanden. Dazu zählen insbesondere die Mechanismen der plastischen Verformung von Metallen, die Gegenstand der aktuellen wissenschaftlichen Debatten sind.
Anwendung

Das klassische und nach wie vor häufigste Anwendungsgebiet der Nanoindentation ist die Härte- und E-Modulbestimmung an Schichtwerkstoffen. Die geringen Kräfte und Eindringtiefen begrenzen die Wechselwirkung mit der indentierten Probe auf sehr kleine Raumvolumina. Dadurch ist es möglich, z. B. sehr dünne Schichten von weniger als 1 µm Dicke ohne nennenswerte Einflüsse des darunter liegenden Substratwerkstoffes zu untersuchen. Weitere Einsatzmöglichkeiten sind die Untersuchung einzelner Körner oder Werkstoffphasen sowie die Aufnahme von Härtegradienten in Randschichten. Da die Nanoindentation eine elektronische und damit kontinuierliche Wegmessung erforderlich macht stehen als Messdaten nicht nur Maximalkraft und Eindringfläche, sondern eine vollständige Kraft-Weg-Kurve zur Verfügung. Diesen zusätzlichen Informationen sind neben unterschiedlichen Härtekennwerten auch Kennwerte zum elastischen Entlastungsverhalten sowie dem Kriechverhalten zu entnehmen. Weiterentwickelte Geräte können z. B. durch zyklische Be- und Entlastung in einer Messung Tiefenprofile der Härte und des E-Moduls sowie Kennwerte zum plastischen Fließverhalten ermitteln. Im Folgenden wird eine Übersicht über die derzeit gängigen Einsatzbereiche gegeben.
Härteprüfung
Bei der makroskopischen Härteprüfung wird eine definierte Kraft für eine definierte Zeitdauer aufgebracht und der verbleibende plastische Eindruck anschließend optisch vermessen. Im Gegensatz dazu wird bei der Nanoindentation die Kraft und die Eindringtiefe kontinuierlich gemessen. Durch Variation der Belastungs- und Entlastungsgeschwindigkeit, der Maximalkraft, der Haltedauer der Maximalkraft und der Belastungsart (z. B. lineare oder quadratische Kraftsteigerung) können eine Vielzahl unterschiedlicher Härtekennwerte und weitere mechanische Kennwerte ermittelt werden.
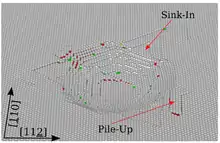
Da man bei den geringen Eindringtiefen der Nanoindentation Abweichungen des Indenters von der geometrischen Idealform (z. B. durch Spitzenverrundung oder Materialanlagerung) nicht vernachlässigen darf, ist die geometrische Form des Indenters über geeignete Prüfverfahren in regelmäßigen zeitlichen Abständen zu bestimmen. Über diese Formfunktion des Indenters kann der Nanoindenter dann zu jeder Eindringtiefe die korrekte Kontaktfläche berechnen. Weitere Besonderheiten der Nanoindentation sind die Berücksichtigung der thermischen Drift, welche über die Wärmeausdehnung von Probe und Indenter aufgrund von Temperaturänderungen einen unter Umständen erheblichen Einfluss auf die gemessene Eindringtiefe haben kann. Die thermische Drift wird in der Regel vor Beginn der Belastung und kurz vor vollständiger Entlastung gemessen. Der ermittelte Wert wird dann aus der Messkurve herausgerechnet. Materialspezifische Besonderheiten bei der Nanoeindringprüfung wie das sink-in oder pile-up werden durch geeignete mathematische Verfahren berücksichtigt.[19]
Bei neueren Geräten ist es möglich, durch Überlagerung des kontinuierlich ansteigenden Kraftsignals während der Belastung mit einem zyklisch schwingendem Kraftsignal kleiner Amplitude (continuouse stiffness measurement - csm) für jeden Zyklus eine eigene Bestimmung von Härte und E-Modul vorzunehmen und so einen Härteverlauf über die Eindringtiefe zu bestimmen.[20]
E-Modul Bestimmung
Aus dem Entlastungsteil der Eindringkurve lässt sich eine dem Elastizitätsmodul verwandte Größe berechnen, die diesem auch in wissenschaftlicher Literatur oft gleichgesetzt wird. Die Methode zur Berechnung dieses Eindringmoduls wurde von Oliver & Pharr[21] entwickelt. Für die Berechnung wird der Teil der Entlastungskurve herangezogen, in dem eine rein elastische Reaktion des Gegenkörpers auf die nachlassende Eindringkraft des Indenters angenommen werden kann.
Die E-Modulbestimmung kann wie die Härtemessung tiefenaufgelöst durch csm-Messung erfolgen. In diesem Fall wird der E-Modul aus der Entlastungskurve des zyklischen Messignals gewonnen, welches stets elastisch sein sollte.
Bei der E-Modulbestimmung ist zu beachten, dass stets ein gewisser Einfluss des Substratmaterials erhalten bleibt, da sich die vom eindringenden Indenter im Material ausbreitenden Spannungsfelder prinzipiell unendlich weit (bei zunehmend geringerer Intensität) ausbreiten und daher überall auch eine elastische Reaktion hervorrufen, die letztlich in die Messung einfließt. Bei tiefenaufgelöster Messung lässt sich der wahre E-Modul einer homogenen Schicht gut abschätzen, indem man die E-Modul vs. Eindringtiefe-Kurve gegen die Eindringtiefe 0 extrapoliert.
Plastisches Fließverhalten
Der Härtewert eines Werkstoffes bei der Härteprüfung ergibt sich aus dem elastischen und plastischen Verformungsverhalten des Werkstoffes. Während der elastische Anteil als singulärer Wert recht einfach aus der Entlastungskurve berechnet werden kann, sind die plastischen Verformungsparameter deutlich aufwendiger zu bestimmen. Dies liegt insbesondere am nichtlinearen Charakter der Fließkurve, wodurch für jeden Wert der Dehnung ein eigener Spannungswert bestimmt werden muss.
Ein wichtiger und vergleichsweise einfach zu bestimmender Kennwert für das plastische Fließen ist die Streckgrenze, welche je nach Indentergeometrie analytisch ermittelt werden kann.[22][23] Zur Bestimmung der weiteren Fließkurve sind Spezialmessungen erforderlich, bei denen ein üblicherweise sphärischer Indenter in einer vorgegebenen Weise in das Material eingedrückt wird. Aus den Messdaten wird dann beispielsweise über FEM-Simulation (Imprintec I3dTest) oder neuronale Netze (ASMEC-Nanoindenter) die Fließkurve bestimmt. Die FEM-Simulation ermöglicht in Kombination mit angepassten Messmethoden dabei auch die Bestimmung der Dehnratenabhängigkeit[24] und der Temperaturabhängigkeit.[25]
Scratchtest
Die meisten Nanoindenter erlauben während des Eindrückens des Indenters in die Probe ein laterales Verfahren des Probentischs, so dass die Indenterspitze durch die Probe „pflügt“. Je nach Gerät ist es möglich Prüfparameter wie Eindringkraft und Verfahrgeschwindigkeit zu variieren sowie Eindringtiefe und laterale Kraft zu messen. Auch ermöglichen es viele Geräte, die gescratchte Strecke vor und nach dem scratchen mit sehr geringer Indenterkraft abzufahren und so für die gesamte Strecke die maximale (elastische & plastische) sowie die bleibende (nur plastische) Tiefe des Scratchgrabens zu bestimmen.
Die Scratchmethode wird mittlerweile für vielfältige Untersuchungen eingesetzt. Beispielsweise ist in der Haftcharakterisierung die Anwendung eines Rampen-Scratches (ein Scratch mit zunehmender Eindringkraft während des scratchens) üblich. Durch Beobachtung, ab welchem Zeitpunkt bzw. welcher Wegstrecke es zu Delaminationen der Schicht kommt kann der zugehörige Kraftwert bestimmt werden und so Schichten bezüglich ihrer Haftfestigkeit verglichen werden. Durch die Kombination von Nanoscratchen und FEM-Simulation kann untersucht werden, unter welchen Lastzuständen es in einem Werkstoff zu Versagen (Enthaftung, Rissbildung) kommt.[26] Dies ermöglicht beispielsweise die Entwicklung von Versagenskriterien für Werkstoffe. Auch die Bestimmung des Reibungskoeffizienzten ist über Scratchtests möglich.
Quellen
- Nanoindentierung, TU-Graz
- Nanoindentierung, Das Fraunhofer-Institut für Schicht- und Oberflächentechnik IST
- Karsten Durst, Mathias Göken (Universität Erlangen-Nürnberg): „Nanoindentierung: Eine Sonde für die lokalen mechanischen Eigenschaften“. (PDF; 6,3 MB) (Memento vom 13. Februar 2006 im Internet Archive)
- Nanoindentierung. (Memento vom 11. Februar 2013 im Webarchiv archive.today) Max-Planck-Institut für Eisenforschung
Literatur
- Karsten Durst: Mikrostrukturelle und mikromechanische Charakterisierung ausscheidungsgehärteter Werkstoffe mit dem nanoindentierenden Rasterkraftmikroskop. 1. Auflage. Der Andere Verlag, Osnabrück 2003, ISBN 3-89959-129-1.
- G. Ziegenhain: Atomistische Simulation von Nanoindentation. 2009, DNB 1002491576.
Einzelnachweise
- G. Ziegenhain: Atomistische Simulation von Nanoindentation. 2009, DNB 1002491576.
- G. Agricola: De Re Metallica. Basel 1556.
- D. Tabor: The Hardness of Metals. Clarendon Press, Oxford 1951.
- R. Feynman: Plenty of Room at the Bottom. In The annual meeting of the American Physical Society at the California Institute of Technology (Caltech, December 29th 1959). In: Caltech’s Engineering and Science. 1960.
- N. Gane, F. Bowden: Microdeformation of Solids. In: Journal of Applied Physics. 39(3), 1968, S. 1432–1436.
- M. Göken, M. Kempf: Pop-ins in Nanoindentations - the Initial Yield Point. In: Zeitschrift fuer Metallkunde. 92(9), 2001, S. 1061–1067.
- Härteprüfung nach Vickers
- A. C. Fischer-Cripps: Nanoindentation. 2. Auflage. Springer, New York 2004.
- A. Gouldstone, N. Chollacoop, M. Dao, J. Li, A. Minor, Y. Shen: Indentation across size scales and disciplines: Recent developments in experimentation and modeling. In: Acta Materialia. 55(12), 2007, S. 4015–4039.
- U. Landman, W. Luedtke, N. Burnham, R. Colton: Atomistic Mechanisms and Dynamics of Adhesion, Nanoindentation, and Fracture. In: Science. 248(4954), 1990, S. 454–461.
- W. D. Nix, H. Gao: Indentation size effects in crystalline materials: A law for strain gradient plasticity. In: Journal of the Mechanics and Physics of Solids. 46(3), 1998, S. 411–426.
- Pan u. a., 2007.
- Chrobak u. a., 2007.
- I. Szlufarska, R. Kalia, A. Nakano, P. Vashishta: A molecular dynamics study of nanoindentation of amorphous silicon carbide. In: Journal of Applied Physics. 102, 2007, S. 023509.
- P. Walsh, R. Kalia, A. Nakano, P. Vashishta, S. Saini: Amorphization and anisotropic fracture dynamics during nanoindentation of silicon nitride: A multimillion atom molecular dynamics study. In: Applied Physics Letters. 77(26), 2000, S. 4332.
- Z. Pan, H. Sun, C. Chen: Colossal Shear-Strength Enhancement of Low-Density Cubic BC 2 N by Nanoindentation. In: Physical Review Letters. 98(13), 2007, S. 135505.
- J. Li: The mechanics and physics of defect nucleation. In: MRS bulletin. 32(2), 2007, S. 151–159.
- Y. Shi, M. L. Falk: Structural transformation and localization during simulated nanoindentation of a noncrystalline metal film. In: Applied Physics Letters. 86(1), 2005, S. 011914.
- Warren C. Oliver, George M. Pharr: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. In: Journal of Materials Research. Band 7, Nr. 6. Springer Nature, Juni 1992, ISSN 0884-2914, S. 1564–1583, doi:10.1557/JMR.1992.1564 (springer.com).
- X. Li, B. Bhushan: Materials Characterization. 48, 2002, S. 11–36.
- W. C. Oliver, G.M. Pharr, J. Mater In: Res. 7, 1992, S. 1564.
- T. F. Juliano, V. M. R. vanLandingham, T. Weerasooriya, P. Moy: Extracting Stress–Strain and Compressive Yield Stress Information From Spherical Indentation. In: Army Research Laboratory Report ARL-TR-4229. 2007, S. 1.
- S. Basu, A. Moseson, M. W. Barsoum In: J. Mater. Res. 21, 2006, S. 2628–2637.
- J. Perne: Plastic flow behavior of (Cr, Al)N hard coatings in dependence of strain rate and nanostructure. In: Thin Solid Films. 556, 2014, S. 390–394.
- K.-D. Bouzakis, M. Pappa, S. Gerardis, G. Skordaris, E. Bouzakis: PVD Coatings’ Strength Properties at Various Temperatures by Nanoindentations and FEM Calculations Determined. In: Tribology in Industry. Vol. 34, No 1, 2012, S. 29–35.
- J. Perne: Experimental and simulative strain field investigation of nano- and microscratches on nanolaminated (Cr, Al)N coating. In: Thin Solid Films. 573, 2014, S. 33–40.