Magneto-optische Falle
Eine magneto-optische Falle (englisch magneto-optical trap, MOT) ist ein Hilfsmittel der Atomphysik, welches zur Kühlung und Speicherung von neutralen Atomen benutzt wird. Kühlung bedeutet hier Abbremsen der Atome, da sich die Temperatur eines einzelnen Atoms durch seine kinetische Energie, also seine Geschwindigkeit ausdrückt. Konkret bedeutet das: Befindet sich eine große Anzahl von Teilchen (Atome, Moleküle etc.) im thermischen Gleichgewicht, so kann die mittlere kinetische Energie eines Teilchens durch eine Temperatur ausgedrückt werden.

Im Gegensatz zur Speicherung von geladenen Teilchen (Ionen), die durch elektrische und magnetische Felder in einer Paul- oder Penning-Falle gefangen werden können, benötigt man für neutrale Atome die optische Kraft, da diese ladungsunabhängig ist. Eine MOT besteht aus sechs paarweise gegenläufigen Laserstrahlen, die die Laserkühlung vornehmen. Zusätzlich benötigt man ein Magnetfeld, um die gekühlten Atome am Platz zu halten. Dabei bewirkt das Magnetfeld eine Zeeman-Aufspaltung der Atomniveaus, die in Verbindung mit den Laserstrahlen zu einer ortsabhängigen Kraft führt.
Die magneto-optische Falle stand am Anfang der experimentellen Forschung zur Bose-Einstein-Kondensation und wird in vielen Experimenten zur Untersuchung von kalten Atomen benutzt.
Funktionsprinzip
Kühlen
Atome werden nach dem Prinzip der Laserkühlung abgekühlt. Das heißt, die Photonen aus den Laserstrahlen übertragen ihren Impuls auf das Atom, das dabei energetisch angeregt wird. Dieser Anregungszustand zerfällt danach spontan oder induziert. Während jedoch bei der stimulierten Emission die Richtung des absorbierten und emittierten Photons gleich sind, ist bei der spontanen Emission die Richtung des emittierten Photons unabhängig von der des absorbierten. Deshalb tragen nur Absorptionsprozesse zur Kühlung bei, bei denen spontane Emission stattfindet (Mittelung über viele Absorptions-Emissions Prozesse). Werden sechs paarweise gegenläufige Strahlen benutzt, wie es oben gezeigt ist, so lassen sich die Atome in allen Raumrichtungen abbremsen und abkühlen. Die folgende Abbildung verdeutlicht den Bremsvorgang schematisch:
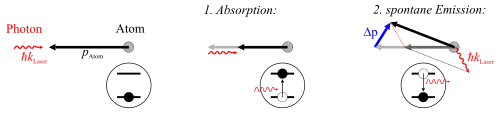
Fangen
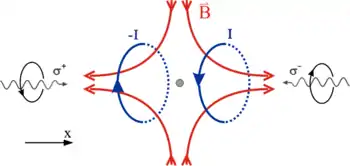
Würde man nur dieses Prinzip anwenden, so erhielte man zwar gekühlte Atome, sie würden aber aus dem Bereich der Kühlung herausdiffundieren, da es nur eine geschwindigkeitsabhängige, aber keine ortsabhängige Kraft gibt. Fügt man nun ein mit dem Abstand zum Kühlbereich linear ansteigendes Magnetfeld hinzu (z. B. mittels einer Anti-Helmholtz-Anordnung von Spulen), so ergibt sich aufgrund der Zeeman-Aufspaltung der Atomzustände, die proportional zum Magnetfeld ist, eine rückstellende Kraft durch den Laser. Aufgrund der Auswahlregeln des Zeeman-Effekts ist es nun nötig, zirkular polarisiertes Licht einzustrahlen, da sonst keine Wechselwirkung mit den Atomzuständen möglich wäre.
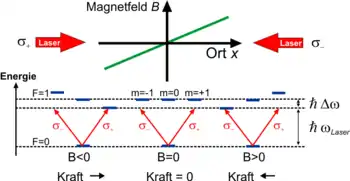
Die Zeichnung rechts erklärt diesen Vorgang genauer für ein einfaches Modellsystem, den (F=0 nach F=1)-Übergang. Das Magnetfeld führt zu einer ortsabhängigen Aufspaltung der Niveaus in einen höheren, einen niedrigeren und einen unveränderten Zustand (mF=±1,0). Da der Laser um Δω gegen die Resonanzfrequenz rotverstimmt ist, kommt er an einer bestimmten Position in Resonanz mit dem abgesenkten bzw. angehobenen Zustand. Links der Kühlregion gibt es einen Punkt, an dem der Kühllaser in Resonanz mit dem abgesenkten Zustand (mF = +1) kommt. Dieser kann aufgrund der Auswahlregeln nur mit Licht der Helizität σ+ interagieren. Dasselbe gilt für σ−-Licht, rechts der Kühlregion mit dem (mF = -1)-Zustand. Strahlt man also von links σ+- und von rechts σ−-Licht ein, so ergibt sich eine Nettokraft, die die Atome in die Kühlregion zurücktreibt.
Die Helizitäten übersetzen sich im Labor in zirkulare Polarisationen, und zwar so, dass ein Paar gegenläufiger Strahlen jeweils gleiche Polarisation hat. Diese Tatsache rührt daher, dass man den Drehsinn des Lichtes einmal in Bezug auf die Ausbreitungsrichtung des Strahles (Polarisation des Lichtes) und einmal in Bezug auf die Quantisierungsachse des Atoms (Helizität σ+, bzw. σ−) betrachtet. Die Quantisierungsachse liegt parallel zum Magnetfeld, an der Stelle x=0 dreht sie sich also um. Für das Atom ist nur der Drehsinn bezüglich dieser Achse von Bedeutung, nicht jedoch die Richtung, aus der das Licht kommt. Damit führt das Drehen der Quantisierungsachse (beim Umkehren des Magnetfeldes) im Bezugssystem des Atoms auch zu einer Änderung des Drehsinnes des Lichtes.
Eine magneto-optische Falle kann nur Atome, die langsamer als eine bestimmte Maximalgeschwindigkeit sind, einfangen. Für schnellere Atome reicht die Bremsung durch die Absorptions-/Emissionszyklen nicht mehr aus und sie werden zwar langsamer, aber nicht gefangen. Dies ist in der folgenden Grafik verdeutlicht, die die Trajektorien (Geschwindigkeit v in Abhängigkeit vom Ort z) von Atomen mit unterschiedlichen Anfangsgeschwindigkeiten zeigt. Zu schnelle Atome werden gebremst, aber nicht gefangen. Das graue Profil gibt das Intensitätsprofil der MOT-Laser an (rechte Koordinatenachse, IS ist die sog. Sättigungsintensität des Übergangs). Das Magnetfeld wurde als linear angenommen, was für die Zentrumsregion einer MOT i. A. eine gute Näherung darstellt.

Reale Atome
Reale Atome haben normalerweise mehrere Zustände, in die das angeregte Atom zerfallen kann, die aber nicht alle mit dem Kühllicht wechselwirken. Um zu verhindern, dass die Atome durch solche Zerfälle aus der Falle verloren gehen, benutzt man je nach atomarer Spezies einen oder mehrere Rückpumplaser, die diese konkurrierenden Zustände wieder in den Kühlprozess zurück transferieren.
Literatur
- Harold J. Metcalf, Peter van der Straten: Laser cooling and trapping. Springer, New York NY u. a. 1999, ISBN 0-387-98747-9 (Graduate Texts in contemporary Physics).
- William D. Phillips: Laser cooling and trapping of neutral atoms. In: Reviews of Modern Physics. 70, 1998, ISSN 0034-6861, S. 721–741.
- E. L. Raab, M. Prentiss, Alex Cable, Steven Chu, D. E. Pritchard: Trapping of neutral sodium atoms with radiation pressure. In: Physical Review Letters. 59, 1987, ISSN 0031-9007, S. 2631–2634, doi:10.1103/PhysRevLett.59.2631.
Weblinks
- Anleitung zu einem Praktikumsversuch an der Universität Colorado (englisch) (Memento vom 10. Juni 2010 im Internet Archive)