Ludwig Schläfli

Ludwig Schläfli (* 15. Januar 1814 in Grasswil, heute zu Seeberg, Kanton Bern; † 20. März 1895 in Bern) war ein Schweizer Mathematiker, der sich mit Geometrie und Funktionentheorie beschäftigte. Er spielte eine Schlüsselrolle bei der Entwicklung des Begriffs der Dimension, welcher unter anderem eine entscheidende Rolle in der Physik spielt. Obwohl seine Ideen heute in jedem Grundstudium in Mathematik behandelt werden, ist Schläfli selbst unter Mathematikern eher unbekannt.

Ludwig Schläfli

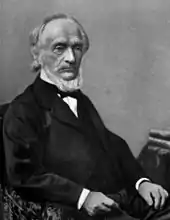
Leben

Schläfli verbrachte den grössten Teil seines Lebens in der Schweiz. Er kam in Grasswil, dem Heimatort seiner Mutter, zur Welt. Kurz darauf zog seine Familie zum nahen Burgdorf, wo sein Vater als Geschäftsmann arbeitete. Ludwig sollte in die Fussstapfen seines Vaters treten, allerdings war er nicht für die praktische Arbeit gemacht.

Auf Grund seiner mathematischen Begabung bekam er 1829 die Möglichkeit, das Gymnasium in Bern zu besuchen. Zu jener Zeit lernte er bereits die Differentialrechnung aus Abraham Gotthelf Kästners Mathematische Anfangsgründe der Analysis des Unendlichen (1761). 1831 begab er sich an die Akademie in Bern, um sich weiter fortzubilden. 1834 wurde aus der Akademie die neue Universität Bern, an der er das Studium der Theologie aufnahm.

Lehre

Nach seinem Abschluss 1836 wurde er zum Lehrer in Thun ernannt. Dieser Beschäftigung ging er bis 1847 nach, wobei er seine Freizeit mit dem Studium der Mathematik und Botanik verbrachte und einmal wöchentlich die Universität in Bern besuchte, um weiter Theologie zu studieren.

Das Jahr 1843 markiert einen Wendepunkt in Schläflis Leben. Schläfli hatte einen Besuch in Berlin geplant, um mit der dortigen mathematischen Gemeinschaft Bekanntschaft zu machen, insbesondere mit Jakob Steiner, einem bekannten Schweizer Mathematiker. Aber unerwarteterweise kam Steiner nach Bern und traf auf Schläfli. Steiner war nicht nur beeindruckt von Schläflis mathematischem Wissen, sondern auch von seinen ausgezeichneten Sprachkenntnissen in Italienisch und Französisch.

Steiner schlug Schläfli vor, seine Berliner Kollegen Carl Gustav Jacob Jacobi, Peter Gustav Lejeune Dirichlet, Karl Wilhelm Borchardt und Steiner selber als Dolmetscher auf der bevorstehenden Reise nach Italien zu unterstützen. Steiner pries diese Idee seinen Freunden in der folgenden Art an (was ein Hinweis darauf ist, dass Schläfli etwas unbeholfen in alltäglichen Angelegenheiten war):

„[…] während er den Berliner Freunden den neugeworbenen Reisegefährten durch die Worte anpries, der sei ein ländlicher Mathematiker bei Bern, für die Welt ein Esel, aber Sprachen lerne er wie ein Kinderspiel, den wollten sie als Dolmetscher mit sich nehmen.“[1]

Schläfli begleitete sie nach Italien und profitierte stark von der Reise. Während des mehr als sechsmonatigen Aufenthalts in Italien übersetzte Schläfli sogar einige Werke der anderen Mathematiker ins Italienische.

Späteres Leben

Schläfli blieb mit Steiner bis 1856 in Kontakt. Die Perspektiven, die ihm eröffnet wurden, ermutigten ihn, sich 1847 für eine Stelle an der Universität Bern zu bewerben. Er wurde 1848 zum Privatdozenten ernannt, 1853 zum ausserordentlichen Professor und 1872 schliesslich zum ordentlichen Professor. Schläflis Lehrtätigkeit dauerte bis zu seiner Emeritierung im Jahr 1891. Bis zu seinem Tod 1895 widmete er sich dem Studium des Sanskrit und der Übersetzung der hinduistischen Schrift Rigveda ins Deutsche.

Höhere Dimensionen

Schläfli ist einer der drei Begründer der mehrdimensionalen Geometrie zusammen mit Arthur Cayley und Bernhard Riemann. Um 1850 war das allgemeine Konzept der euklidischen Räume noch nicht entwickelt – aber lineare Gleichungen in Variablen wurden bereits gut verstanden. In den 1840er Jahren entwickelte William Rowan Hamilton seine Quaternionen und John Thomas Graves und Cayley die Oktaven. Diese beiden Systeme arbeiteten mit einer Basis von vier bzw. acht Elementen und legten eine Interpretation analog zu den kartesischen Koordinaten des dreidimensionalen Raums nahe.

Von 1850 bis 1852 arbeitete Schläfli an seinem Hauptwerk Theorie der vielfachen Kontinuität, in dem er das Studium der linearen Geometrie des -dimensionalen Raums begründete. Er definierte auch die -dimensionale Sphäre und berechnete ihr Volumen. Er beschloss, sein Werk zu publizieren, und sandte es der Akademie in Wien zu, aber es wurde aufgrund seines Umfangs abgelehnt. Ein zweiter Versuch in Berlin endete mit demselben Ergebnis. Schliesslich wurde Schläfli 1854 gebeten, eine kürzere Version zu schreiben, was er aber nicht tat. Steiner versuchte ihm dabei zu helfen, das Werk in Crelles Journal zu veröffentlichen. Aber aus unbekannten Gründen kam dies auch nicht zustande. Teile des Werkes wurden 1860 von Cayley auf Englisch veröffentlicht. Die erste Veröffentlichung der gesamten Schrift erfolgte erst 1901 nach Schläflis Tod. Die erste Rezension des Buches erschien 1904 im niederländischen Mathematikjournal Nieuw Archief voor de Wiskunde und wurde vom niederländischen Mathematiker Pieter Hendrik Schoute verfasst.

Ein Auszug aus der Einleitung zur Theorie der vielfachen Kontinuität:

„Anzeige einer Abhandlung über die Theorie der vielfachen Kontinuität
Die Abhandlung, die ich hier der Kaiserlichen Akademie der Wissenschaften vorzulegen die Ehre habe, enthält einen Versuch, einen neuen Zweig der Analysis zu begründen und zu bearbeiten, welcher, gleichsam eine analytische Geometrie von Dimensionen, diejenigen der Ebene und des Raumes als spezielle Fälle für in sich enthielte. Ich nenne denselben Theorie der vielfachen Kontinuität überhaupt in demselben Sinne, wie man zum Beispiel die Geometrie des Raumes eine Theorie der dreifachen Kontinuität nennen kann. Wie in dieser eine Gruppe von Werten der drei Koordinaten einen Punkt bestimmt, so soll in jener eine Gruppe gegebener Werte der Variabeln eine Lösung bestimmen. Ich gebrauche diesen Ausdruck, weil man bei einer oder mehreren Gleichungen mit vielen Variabeln jede genügende Gruppe von Werten auch so nennt; das Ungewöhnliche der Benennung liegt nur darin, daß ich sie auch noch beibehalte, wenn gar keine Gleichung zwischen den Variabeln gegeben ist. In diesem Falle nenne ich die Gesamtheit aller Lösungen die -fache Totalität; sind hingegen Gleichungen gegeben, so heißt bzw. die Gesamtheit ihrer Lösungen -faches, -faches, -faches, […] Kontinuum. Aus der Vorstellung der allseitigen Kontinuität der in einer Totalität enthaltenen Lösungen entwickelt sich diejenige der Unabhängigkeit ihrer gegenseitigen Lage von dem System der gebrauchten Variabeln, insofern durch Transformation neue Variabeln an ihre Stelle treten können. Diese Unabhängigkeit spricht sich aus in der Unveränderlichkeit dessen, was ich den Abstand zweier gegebener Lösungen (), () nenne und im einfachsten Fall durch

definiere, indem ich gleichzeitig das System der Variabeln ein orthogonales heiße, […]“

Schläfli fasste Punkte im -dimensionalen Raum zuerst als Lösungen von linearen Gleichungen auf, um dann den brillanten Gedankengang auszuführen, ein System ohne Gleichungen zu betrachten, um dadurch alle möglichen Punkte des (wie wir es heute nennen würden) zu erhalten. Er verbreitete dieses Konzept in den Artikeln, die er in den 1850er und 1860er Jahren publizierte, und es entwickelte sich schnell. 1867 begann er einen Artikel mit den Worten Wir betrachten den Raum der -Tupel von Punkten. […]. Dies deutet nicht nur darauf hin, dass er die Theorie in den Griff bekommen hatte, sondern auch, dass sein Publikum keine langen Erklärungen mehr nötig hatte.

Polytope

In der Theorie der vielfachen Kontinuität definiert Schläfli sogenannte Polyschemas, welche heutzutage Polytope genannt werden. Sie sind die mehrdimensionalen Analoga der Polygone und Polyeder. Er entwickelte deren Theorien und fand unter anderem die mehrdimensionale Variante des Eulerschen Polyedersatzes. Er bestimmte auch die regulären Polytope, d. h. die -dimensionalen Verwandten der regulären Polygone und der Platonischen Körper. Es stellte sich heraus, dass es deren sechs im vierdimensionalen Raum und drei in allen höher dimensionalen Räumen gibt.

Obwohl Schläfli in der zweiten Hälfte des 19. Jahrhunderts ziemlich bekannt bei seinen Kollegen, im Speziellen für seine Beiträge zur komplexen Analysis, war, bekam sein frühes geometrisches Werk lange Zeit keine grosse Aufmerksamkeit. Zu Beginn des 20. Jahrhunderts befasste sich Pieter Hendrik Schoute zusammen mit Alicia Boole Stott mit Polytopen. Sie bewies Schläflis Resultat über reguläre Polytope noch einmal, allerdings nur für den vierdimensionalen Raum, und entdeckte danach Schläflis Buch. Später studierte Willem Abraham Wijthoff semi-reguläre Polytope. Seine Arbeit wurde von H. S. M. Coxeter, John Horton Conway und anderen fortgesetzt. Es gibt immer noch viele ungelöste Probleme in diesem Bereich, der auf der Arbeit von Ludwig Schläfli gründet.

Trivia
  • Das Schläfli-Symbol ist nach Ludwig Schläfli benannt.
  • Ludwig Schläfli sollte wie sein Vater Geschäftsmann werden. Aber er machte die denkbar schlechtesten Geschäfte, da er nicht begreifen konnte, dass man einen Gegenstand teurer verkaufte, als dass man ihn einkaufte.[2]
  • Schläfli machte ein theologisches Staatsexamen und war (nach einigen Komplikationen mit der Probepredigt[2]) im Berner Verzeichnis der zum Pfarramt berechtigten Personen zu finden. Er hat aber ein solches wohl nie innegehabt.
  • In der Bibliothek Exakte Wissenschaften der Universität Bern erinnert der Schriftzug Three quarks for Muster Mark, Einstein und Schläfli an Schläflis Tätigkeit in Bern.

Literatur

Einzelnachweise
  1. Moritz Cantor: Schläfli, Ludwig. In: Allgemeine Deutsche Biographie (ADB). Band 54, Duncker & Humblot, Leipzig 1908, S. 29–31.
  2. Moritz Cantor: Schläfli, Ludwig. In: Allgemeine Deutsche Biographie (ADB). Band 54, Duncker & Humblot, Leipzig 1908, S. 29–31.
Normdaten (Person): GND: 118795082 | LCCN: no2001080371 | VIAF: 113316205 |
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.