Lagrange-Kreisel

Lagrange-Kreisel unterscheiden sich kreiseltheoretisch nur in drei Größen:

1. dem axialen Trägheitsmoment C = Θ₃ um die Figurenachse,
2. dem äquatorialen Trägheitsmoment A = Θ₁ = Θ₂ um dazu senkrechte Achsen und
3. dem Stützpunktmoment[1]^:89 c₀ = mg s, das sich aus dem Abstand s zwischen Stützpunkt und Schwerpunkt und der Gewichtskraft mg des Kreisels ergibt.

Bei der Bewegung des Lagrange-Kreisels gibt es die folgenden Integrale der Bewegung, die in der Kreiseltheorie kurz Integrale genannt werden:

Gesamtenergie E des Kreisels

Sie setzt sich aus der Lage- und der Rotationsenergie zusammen. Das Schwerefeld der Erde ist konservativ und die Kreiselbewegung befolgt somit den Energieerhaltungssatz.

Drehimpuls L_z um die Lotlinie

Dieser ist konstant, weil die Lotlinie parallel zur Gewichtskraft ist, deren Moment daher den Drehimpuls L_z nicht verändern kann.

Axialer Drehimpuls L₃ um die Figurenachse

Dieser ist konstant, weil der Schwerpunkt des Lagrange-Kreisels per definitionem auf der Figurenachse liegt und das Moment der Gewichtskraft senkrecht zu ihrem Hebelarm ist, der hier vom Stützpunkt zum Schwerpunkt weist. Daher kann sich der Endpunkt des Drehimpulsvektors nur in einer Ebene senkrecht zur Figurenachse bewegen, siehe auch Winkelgeschwindigkeit und Drehimpuls beim symmetrischen Kreisel. Somit ist die Komponente L₃ im körperfesten System konstant.[3]^:110[1]^:95[4]^:155

Dissipative Einflüsse wie Reibung werden, wenn nicht ausdrücklich erwähnt, vernachlässigt. Alle Lagrange-Kreisel, die in A, C, c₀, E, L_z und L₃ übereinstimmen und aus gleichen Ausgangspositionen starten zeigen identisches Verhalten.

Um die Locuskurve zu analysieren, reicht es aus, Kugelkreisel mit A = Θ₁ = Θ₂ = Θ₃ = C zu betrachten, deren Trägheitsmomente also gleich dem äquatorialen Trägheitsmoment A eines interessierenden Kreisels sind. Denn alle Kreisel die denselben Drehimpuls besitzen und in den Größen A, c₀ sowie einer Konstanten k übereinstimmen, die potentielle- und kinetische Energien kombiniert, zeigen bei gleicher Ausgangsposition gleiche Locuskurven. Diese sich ähnelnden Kreisel – und dazu gehören auch besagte Kugelkreisel – werden einander homolog genannt. Die Analyse von Kugelkreiseln ist in dieser Hinsicht gleichzeitig einfacher und allgemeiner. Die Gemeinsamkeiten aller homologen Lagrange-Kreisel beschränken sich allerdings auf die Locuskurve und schließen insbesondere nicht den Eigendrehwinkel φ um die Figurenachse ein. Die Differenz der entsprechenden Eigendrehgeschwindigkeit zwischen zwei homologen Kreiseln ist jedoch immer konstant. Diese Ähnlichkeiten in den Kreiselbewegungen fiel erstmals Gaston Darboux auf.[8]

Zentral bei der Diskussion der Bewegungen eines Lagrange-Kreisels ist die Locuskurve, auf der sich der Durchstoßpunkt der Figurenachse durch die Einheitskugel um den Stützpunkt, der Locus der Figurenachse, bewegt. Als Orientierungshilfe werden an dieser Kugel Bezeichnungen aus der Geographie übernommen: Der obere Totpunkt liegt im Nordpol und der untere Totpunkt im Südpol der Kugel. Die horizontale Ebene durch den Stützpunkt schneidet die Kugel am Äquator und ein zu ihm paralleler Kleinkreis der Kugel wird Breitenkreis genannt. Ein halber Großkreis, der den Nordpol und Südpol verbindet heißt Meridian.

Zur Darstellung der Locuskurven von hängenden Kreiseln in den Abbildungen 3 und 4 wurde eine stereografische Projektion verwendet. Das Projektionszentrum ist über dem Stützpunkt × und der Bildebene im Nordpol der Kugel.

Alternativ werden auch perspektivische Ansichten wie in Abb. 5 benutzt.

Abb. 2: Waagerecht im Kreis (entlang der roten Ellipse R) präzedierendes Speichenrad (fett schwarz)

Bei der Bewegung des Lagrange-Kreisels folgt der axiale Drehimpuls L₃ der Figurenachse. Dem Drallsatz zufolge entsteht daher beim Richtungswechsel der Figurenachse eine Kreiselwirkung, die dieser Bewegung genau entgegengesetzt ist.

Dieser Mechanismus ermöglicht die paradoxe Bewegung des waagerechten Kreisels, bei dem sich die Figurenachse in der horizontalen Ebene bewegt, siehe Abb. 2. Hier ist die besagte Kreiselwirkung horizontal orientiert und wenn diese gerade so groß ist, dass sie das immer horizontale Moment der Gewichtskraft ausgleicht, bleibt die Figurenachse in der horizontalen. Die Bedingung für diese besondere reguläre Präzession ist L_z · L₃ = A · c₀, siehe #Reguläre Präzession.

Im Allgemeinen besitzt die Kreiselwirkung jedoch eine horizontale und eine vertikale Komponente. Letztere wird durch kein äußeres Moment ausgeglichen, sodass der Kreisel durch die vertikale Kreiselwirkung ablenkt wird. Der Kreisel weicht dabei soweit aus, bis in der horizontalen ein dynamisches Gleichgewicht mit der Gewichtskraft gefunden ist[7]^{:204 f}.

• 
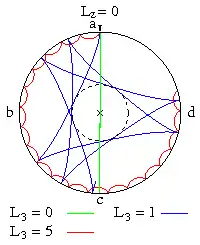  Abb. 3: Locuskurven ohne vertikalen Drehimpuls[9]
• 
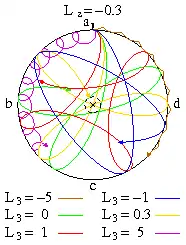  Abb. 4: Locuskurven mit negativem vertikalen Drehimpuls[9]

Die Abb. 3 zeigt Kreiselbewegungen ohne vertikalen Drehimpuls, wo die Umrundung des Südpols ausschließlich durch die oben beschriebene Kreiselwirkung hervor gerufen wird. Im Fall L₃ = 0 entspricht der Kreisel einem sphärischen Pendel, das zwischen den Punkten a, dem Südpol und c hin und her schwingt (senkrechte grüne Linie). Mit zunehmendem axialen Drehimpuls wird durch dessen Bewegung die Figurenachse immer stärker in Bewegungsrichtung rechts abgelenkt. Wird L₃ größer als etwa 10, werden die durchlaufenen Bögen so klein, dass sie mit dem Auge nicht mehr als solche erkennbar sind. Diese dann regelmäßig erscheinende Bewegung wird pseudoreguläre Präzession genannt und führt hier am Äquator abcd entlang.

Durch einen Drehstoß in horizontaler Richtung im Uhrzeigersinn bekommt das sphärische Pendel einen Drehimpuls L_z = -0,3, siehe Abb. 4 grüne Kurve. Bei L₃ = -L_z schwingt der Kreisel durch den Südpol (gelbe Kurve). Die Schleifen, die bei L₃ > -L_z auftreten, werden auch hier mit L₃ > 10 so klein, dass sie mit dem Auge nicht mehr als solche erkennbar sind und der Kreisel eine pseudoreguläre Präzession entlang des Äquators zeigt. Bekommt der Kreisel einen Drehimpuls L₃ < -L_z, dann wird er in Bewegungsrichtung so weit nach links abgelenkt, dass er den unteren Totpunkt verfehlt. Bei ${\displaystyle L_{3}={\tfrac {Ac_{0}}{L_{z}}}=-3{\tfrac {1}{3}}}$ kann er in regulärer Präzession am Äquator adcb entlang laufen (schwarzer Kreis). Unterhalb dieses Wertes liegt die Locuskurve in der Nordhalbkugel, zeigt dort zunächst Wellen, später Spitzen und schließlich Schleifen. Ab L₃ < -10 sind diese Schleifen wieder so klein, dass eine pseudoreguläre Präzession entlang des Äquators stattfindet.

Abb. 5: Locuskurven eines aufrechten Lagrange-Kreisels[10]

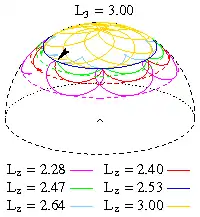
Abbildung 5 zeigt Locuskurven eines aufrechten Lagrange-Kreisels, dessen Bewegung beim schwarzen Pfeil beginnt. Die Locuskurven zeigen Schleifen (lila und gelb), Spitzen (hellrot und hellblau) oder Wellen (grün). Bei L_z ≈ 2,53 findet eine langsame reguläre Präzession statt (blauer Breitenkreis) und bei L_z ≈ L₃ erreicht der Kreisel den oberen Totpunkt (gelbe Schleifen). Bei zunehmendem L_z > L₃ umschlingen die Schleifen den Nordpol und die Kugel immer weiter und nähern sich von Norden dem blauen Breitenkreis an, in dem dann schließlich eine schnelle reguläre Präzession stattfindet. Weitere Zunahme von L_z liefert immer größere Schleifen, die den blauen Breitenkreis von süden und einen südlicheren Breitenkreis von Norden tangieren. Mit L_z → ∞ nähert sich der südliche tangierte Breitenkreis dem am Äquator gespiegelten blauen Breitenkreis an und die Locuskurve wird zu einem Großkreis, der diese beiden Breitenkreise tangiert.[7]^{:255 f}

Wenn der Drehimpuls hinreichend groß und nahe der Figurenachse ausgerichtet ist, findet auch beim aufrechten Kreisel eine pseudoreguläre Präzession statt.

Die pseudoreguläre Präzession ist der wichtigste Punkt der Theorie des Lagrange-Kreisels und hat ob der Häufigkeit ihres Auftretens und ihrer paradoxen Eigenschaften größtes Interesse seitens der Naturphilosophie auf sich gezogen[7]^:209. Die Phänomenologie zeigt, dass sich die Locuskurve des Lagrange-Kreisels bei großem axialen Drehimpuls oft auf Schleifen zwischen zwei Breitenkreisen bewegt, siehe Locuskurven in Abhängigkeit von L₃. Bei der pseudoregulären Präzession nähern sich die beiden Breitenkreise ohne zusammen zu fallen so weit an, dass sie mit dem Auge nicht mehr voneinander getrennt und die Schleifen nicht mehr als solche wahrgenommen werden können. Die Bewegung sieht dann aus wie eine reguläre Präzession, ist aber keine und wird nach Felix Klein und Arnold Sommerfeld[7]^:209,291 pseudoreguläre Präzession genannt.

Die reguläre Präzession kann nur bei ganz bestimmten Anfangsbedingungen entstehen, wohingegen die pseudoreguläre beliebige Anfangsbedingungen erlaubt[3]^:120, solange der anfängliche Drehimpuls L nahe an der Figurenachse ausgerichtet ist und hinreichend groß, also etwa L² > 100 A c₀, ist[7]^{:291 f}.

Weil sich die Figurenachse nur in der Nähe des Drehimpulsvektors befindet, umläuft sie diesen rasch auf engem Kegel. Diese Erzitterungen der Figurenachse werden nach einem der Astronomie entlehnten Wort Nutationen genannt[1]^{:63 ff}. Der Umlauf der Figurenachse eines Kreisels um den Drehimpulsvektor kann durch eine Zykloide in einer Tangentialebene an die Einheitskugel angenähert werden, was im Hauptartikel nachzugeschlagen ist.

Beim schnellen Kreisel dominiert seine Rotationsenergie über seine potentielle Energie. Wenn bei gleichen Anfangsbedingungen des Kreisels die Winkelgeschwindigkeit um die Figurenachse auf das n-fache gesteigert wird, dann ist die Trajektorie des Kreisels identisch mit der des Kreisels mit der ursprünglichen Winkelgeschwindigkeit, bei dem die Schwerebeschleunigung jedoch durch n² geteilt wurde. Im ersteren Fall großer Winkelgeschwindigkeit wird die Trajektorie n-mal schneller durchlaufen. Entsprechend zeigt der schnelle schwere Kreisel asymptotisch für ω → ∞ das gleiche Verhalten wie der kräftefreie Euler-Kreisel.[4]^{:161 ff}

Für die analytische Lösung der Bewegungsgleichungen wird die Kreiselbewegung mit Euler-Winkeln ψ, ϑ und φ dargestellt, siehe Euler-Winkel in der Kreiseltheorie. Mit deren Zeitableitungen können die Winkelgeschwindigkeit, die Gesamtenergie und die konstanten Drehimpulse um die Figurenachse und die Lotlinie ausgedrückt werden. So liegen also drei Gleichungen in drei unbekannten Winkeln vor, die in diesem Fall gestatten den Neigungswinkel ϑ auszurechnen, wobei elliptische Integrale entstehen, die von elliptischen Funktionen gelöst werden.

Für den Winkel ϑ ergibt sich mit der Konstanten

${\displaystyle k:=2AE+\left(1-{\tfrac {A}{C}}\right)L_{3}^{2}}$

und u := cosϑ die autonome Differentialgleichung

${\displaystyle {\dot {u}}^{2}=U(u):={\frac {1}{A^{2}}}[(k-L_{3}^{2}-2c_{0}Au)(1-u^{2})-(L_{z}-L_{3}u)^{2}]}$

Die Kreiselfunktion[3]^:122[1]^:104 U ist ein Polynom dritten Grades in u. Im physikalisch relavanten Bereich muss U(u) ≥ 0 und |u| ≤ 1 sein. Falls L₃ und L_z betraglich gleich sind, ist u = 1 oder u = -1 eine Nullstelle von U und somit kann die Figurenachse die Senkrechte erreichen. Wenn L_z ≠ L₃, ist wegen U(1) < 0 und U(∞) > 0 eine Nullstelle größer als eins. Das Vorzeichen von ${\displaystyle {\dot {u}}}$ ergibt sich nach dem bei Schwingungen üblichen Verfahren. Die Variable u bewegt sich im Intervall [-1, 1] zwischen zwei Extremen, zwischen denen das Polynom U positiv ist und in denen U = 0 ist. In diesen Nullstellen wechselt ${\displaystyle {\dot {u}}}$ sein Vorzeichen.

Die Bewegungsfunktion folgt nach Trennung der Variablen[7]^{:222 f.}:

${\displaystyle {\begin{aligned}t(\vartheta )=&\int {\frac {\mathrm {d} u}{\sqrt {U(u)}}}\\\psi (\vartheta )=&\int {\underline {\frac {L_{z}-L_{3}u}{A(1-u^{2})}}}{\frac {\mathrm {d} u}{\sqrt {U(u)}}}\\\varphi (\vartheta )=&\int {\underline {\left[{\frac {L_{3}-L_{z}u}{A(1-u^{2})}}+L_{3}\left({\frac {1}{C}}-{\frac {1}{A}}\right)\right]}}{\frac {\mathrm {d} u}{\sqrt {U(u)}}}\end{aligned}}}$

Der Bruch ${\displaystyle {\tfrac {\mathrm {d} u}{\sqrt {U(u)}}}}$ ist gleich dem Differential der Zeit dt und die unterstrichenen Terme sind die Winkelgeschwindigkeiten zu den Winkeln ψ und φ. Der Winkel ϑ ergibt sich aus der Umkehrung der Funktion t( ϑ ). Auf den rechten Seiten stehen sogenannte elliptische Integrale, deren Lösungen elliptische Funktionen sind.

Die Wahl des Vorzeichens der Wurzel in den Nennern der Integranden hängt vom Integrationsintervall ab. Bei der Integration über ein nullstellenfreies Intervall [u₀, u₁] ist für die Wurzel in den Nennern das Vorzeichen der Differenz u₁ − u₀ zu nehmen. Deswegen liefern die Integrale über ein Intervall [u₀, u₁] dasselbe Ergebnis, wie bei Integration über das Intervall [u₁, u₀]. Das erklärt die Symmetrieeigenschaften der Locuskurven, die aus Stücken zusammengesetzt sind, die kongruent oder spiegelbildlich zueinander sind.

Der Neigungswinkel ϑ berechnet sich speziell aus[3]^:113

${\displaystyle {\begin{aligned}\cos \vartheta =&u=u_{0}+(u_{1}-u_{0})\operatorname {sn} ^{2}\left({\sqrt {\frac {c_{0}(u_{2}-u_{0})}{2A}}}(t-t_{0});k\right)\\K(k)=&\int _{0}^{\frac {\pi }{2}}{\frac {\mathrm {d} x}{\sqrt {1-k^{2}\sin ^{2}(x)}}}\\T=&2K(k){\sqrt {\frac {2A}{c_{0}(u_{2}-u_{0})}}}\end{aligned}}}$

Darin sind sn(z; k) die Jacobische elliptische Funktion sinus amplitudinis, u_0,1,2 die drei nach Größe sortierten Nullstellen der Kreiselfunktion und ${\displaystyle k:={\sqrt {\tfrac {u_{1}-u_{0}}{u_{2}-u_{0}}}}}$ das elliptische Modul. Das dimensionslose elliptische Modull tritt nur im vollständigen elliptischen Integral K und der elliptischen Funktion sn auf und darf nicht mit der kinetischen Konstante k verwechselt werden, die die Dimension M² L⁴ T ^–2 besitzt. Die Funktion sn(z; k) hat die Periode 4K und der Winkel ϑ die Periode T. Diese Zeit verstreicht zwischen zwei Berührungen der Locuskurve mit dem südlichen Breitenkreis bei ${\displaystyle \cos \vartheta =u_{0}}$. Die Winkel ψ und φ ergeben sich als Linearkombination zweier Legendre-Integrale Π der dritten Art[7]^{:267 f}.

Darstellung des Neigungswinkels mit elliptischen Funktionen
Darstellung des Neigungswinkels mit dem sinus amplitudinis sn
Die Kreiselfunktion wird durch ihre drei Nullstellen u0,1,2 ausgedrückt, für die -1 < u0 < u1 < +1 < u2 angenommen wird[3]:111: ${\displaystyle {\dot {u}}^{2}=U(u)={\frac {2c_{0}}{A}}(u-u_{0})(u-u_{1})(u-u_{2})}$ Im Bereich -∞ < u ≤ u0 sowie u1 ≤ u < u2 ist die Kreiselfunktion negativ ansonsten positiv. Im Intervall u ∈ [ u0, u1 ] liefert die Substitution ${\displaystyle \sin ^{2}(v):={\tfrac {u-u_{0}}{u_{1}-u_{0}}}}$ die Faktoren ${\displaystyle {\begin{aligned}u-u_{0}=&(u_{1}-u_{0})\sin ^{2}(v)\\u-u_{1}=&-(u_{1}-u_{0})\cos(v)^{2}\\u-u_{2}=&-(u_{2}-u_{0})\left(1-{\frac {u_{1}-u_{0}}{u_{2}-u_{0}}}\sin ^{2}(v)\right)\end{aligned}}}$ und mit dem elliptischen Modul ${\displaystyle k^{2}={\tfrac {u_{1}-u_{0}}{u_{2}-u_{0}}}}$ (nicht zu verwechseln mit der kinetischen Konstante k) die Zeitableitungen ${\displaystyle {\begin{aligned}{\dot {u}}=&{\sqrt {U(u)}}=(u_{1}-u_{0})\sin(v)\cos(v){\sqrt {{\frac {2c_{0}}{A}}(u_{2}-u_{0})\left(1-k^{2}\sin ^{2}(v)\right)}}\\{\frac {\mathrm {d} }{\mathrm {d} t}}\sin ^{2}(v)=&2\sin(v)\cos(v){\dot {v}}={\frac {\dot {u}}{u_{1}-u_{0}}}\\\rightarrow {\dot {v}}=&{\sqrt {{\frac {c_{0}}{2A}}(u_{2}-u_{0})\left(1-k^{2}\sin ^{2}(v)\right)}}\end{aligned}}}$ Das führt nach Trennung der Variablen auf die Legendre-Form eines elliptischen Integrals erster Art:[2]:263 ff. ${\displaystyle {\begin{aligned}z(v):=&\int _{0}^{v}{\frac {\mathrm {d} \vartheta }{\sqrt {1-k^{2}\sin(\vartheta )^{2}}}}={\sqrt {{\frac {c_{0}}{2A}}(u_{2}-u_{0})}}(t-t_{0})\end{aligned}}}$ Hier wurde angenommen, dass der Kreisel zur Zeit t0 am Breitenkreis u = u0, also mit ${\displaystyle v=0}$, startet. Die Jacobische elliptische Funktion sn hat die Eigenschaft sn(z(v);k) = sin(v) was die im Text stehende Lösungsfunktion ergibt.
Darstellung des Neigungswinkels mit der Weierstraßschen ℘-Funktion
Die Differentialgleichung ${\displaystyle {\dot {u}}^{2}=U(u)}$ lässt sich mittels ${\displaystyle u={\tfrac {2A}{c_{0}}}x+{\tfrac {k}{6Ac_{0}}}}$ in die Form ${\displaystyle {\dot {x}}^{2}=4x^{3}-g_{2}x-g_{3}}$ bringen, die durch die Weierstraß’sche ℘-Funktion erfüllt wird. Darin sind ${\displaystyle {\begin{aligned}g_{2}=&{\frac {k^{2}+12A^{2}c_{0}^{2}-12AL_{z}L_{3}c_{0}}{12A^{4}}}\\g_{3}=&{\frac {{\big (}k^{2}-18Ac_{0}(2Ac_{0}+L_{z}L_{3}){\big )}k+54A^{2}c_{0}^{2}(L_{z}^{2}+L_{3}^{2})}{216A^{6}}}\end{aligned}}}$ Bewegungskonstanten.[11]

Wie im Abschnitt #Bewegungsfunktion des Lagrange-Kreisels bereits dargelegt, ist eine Nullstelle der Kreiselfunktion größer als eins. Nur die beiden anderen Nullstellen u_1,2 = cosϑ_1,2 können den Locus bestimmen, der sich entsprechend zwischen zwei Extremen aufhält. In diesen Extremen verschwindet die Kreiselfunktion (U = 0.)

Wegen ${\displaystyle {\dot {\psi }}={\tfrac {L_{z}-L_{3}u}{A(1-u^{2})}}}$ bestimmt die Nullstelle e des Zählers, mit L_z − L₃e = 0, die Form der Locuskurve:

1. Liegt e außerhalb des physikalisch erreichbaren Bereichs, dann ist überall ${\displaystyle {\dot {\psi }}<0}$ oder ${\displaystyle {\dot {\psi }}>0}$ und die Locuskurve ist wellenförmig und ähnelt einer verkürzten Zykloide.
2. Ist e innerhalb des physikalisch erreichbaren Bereichs, dann wechselt dort ${\displaystyle {\dot {\psi }}}$ das Vorzeichen und die Locuskurve gleicht einer verlängerten Zykloide mit Schleifen.
3. Fällt e mit einer der Nullstellen von U zusammen, dann ist dort ${\displaystyle {\dot {\psi }}={\dot {\vartheta }}=0}$ und die Locuskurve erscheint wie eine gewöhnliche Zykloide mit Spitzen. Das entspricht dem Fall, wo die Figurenachse aus der Ruhe losgelassen wird.[12]

Bei der regulären Präzession ist ϑ genauso wie u und die Winkelgeschwindigkeiten ${\displaystyle {\dot {\psi }},{\dot {\varphi }}}$ konstant. Mit den Drehimpulskomponenten

${\displaystyle {\vec {L}}=L_{v}{\hat {e}}_{z}+L_{f}{\hat {e}}_{3},\;L_{v}={\frac {L_{z}-L_{3}u}{1-u^{2}}},\;L_{f}={\frac {L_{3}-L_{z}u}{1-u^{2}}}}$

stellt sie sich ein, wenn

${\displaystyle Ac_{0}=L_{v}L_{f}={\frac {L_{z}-L_{3}u}{1-u^{2}}}{\frac {L_{3}-L_{z}u}{1-u^{2}}}}$

In den Euler-Winkeln schreibt sich das

${\displaystyle C{\dot {\psi }}{\dot {\varphi }}+(C-A){\dot {\psi }}^{2}u=c_{0}}$

Bei der regulären Präzession erfüllen die Konstanten diese Bedingung. Die Bedingung ist symmetrisch in L₃ und L_z, denn die Bedingung bleibt erfüllt, wenn die beiden Drehimpulse ihre Werte tauschen. Die Bewegungsgleichungen können bei der regulären Präzession nicht mit den elliptischen Integralen oben gelöst werden, weil die Integrationsintervalle null Ausdehnung besitzen. Jedoch können die Winkelgeschwindigkeiten ${\displaystyle {\dot {\psi }},{\dot {\vartheta }},{\dot {\varphi }}}$ weil sie konstant sind direkt integriert werden zu

${\displaystyle {\begin{aligned}\vartheta =&\arccos(u)\\\psi =&{\frac {L_{z}-L_{3}u}{A(1-u^{2})}}t+\psi _{0}\\\varphi =&L_{3}\left({\frac {1}{C}}-{\frac {1}{A}}\right)t+{\frac {L_{3}-L_{z}u}{A(1-u^{2})}}t+\varphi _{0}\end{aligned}}}$

worin ψ₀ und φ₀ der Anpassung an Anfangsbedingungen bei t = 0 dienen.

Die reguläre Präzession ist eine stabile Bewegungsform.

• 
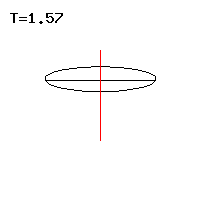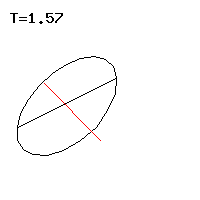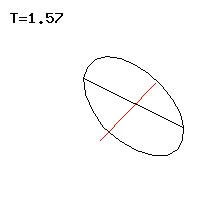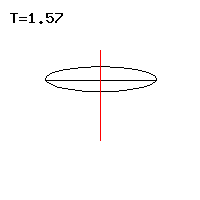  Abb. 7: Schnelle reguläre Präzession
• 
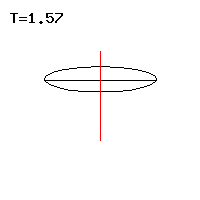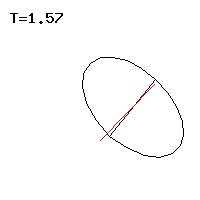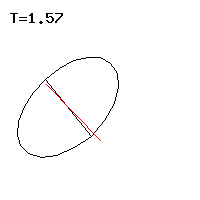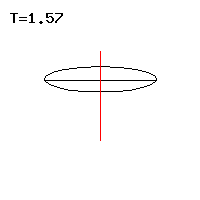  Abb. 8: Langsame reguläre Präzession

Zu gegebenem Richtungskosinus u und Drehimpuls L₃ um die Figurenachse gibt es höchstens zwei Winkelgeschwindigkeiten ${\displaystyle {\dot {\psi }}}$, die mit einer regulären Präzession verträglich sind.

Denn dann ist die Bedingung ${\displaystyle c_{0}=C{\dot {\psi }}{\dot {\varphi }}+(C-A){\dot {\psi }}^{2}u}$ wegen ${\displaystyle {\dot {\varphi }}=\omega _{3}-{\dot {\psi }}u}$ eine quadratische Gleichung in ${\displaystyle {\dot {\psi }}}$ mit den Lösungen:[3]^:120

${\displaystyle {\dot {\psi }}_{1,2}={\frac {L_{3}}{2Au}}\left(1\pm {\sqrt {1-{\frac {4c_{0}Au}{L_{3}^{2}}}}}\right)\approx {\begin{cases}{\frac {L_{3}}{Au}}\\{\frac {c_{0}}{L_{3}}}\end{cases}}}$

Die rechte Näherung gilt für den schnellen Kreisel, wo ${\displaystyle L_{3}^{2}\gg 4Ac_{0}u}$ ist. Die schnelle Präzession des ersten Falls entspricht demnach der Nutation des kräftefreien Euler-Kreisels, die proportional zum axialen Drehimpuls ist, siehe Abb. 7. Bei der langsamen Präzession im zweiten Fall ist die Präzessionsgeschwindigkeit umgekehrt proportional zum axialen Drehimpuls, siehe Abb. 8.

Die Euler-Poisson-Gleichungen sind die spezifischen Bewegungsgleichungen für den schweren Kreisel mit Stützpunkt und nehmen beim Lagrange-Kreisel die Form

${\displaystyle {\begin{aligned}&A{\dot {\omega }}_{1}+(C-A)\omega _{2}\omega _{3}={\dot {L}}_{1}+\left({\frac {1}{A}}-{\frac {1}{C}}\right)L_{2}L_{3}=c_{0}n_{2}\\&A{\dot {\omega }}_{2}+(A-C)\omega _{3}\omega _{1}={\dot {L}}_{2}+\left({\frac {1}{C}}-{\frac {1}{A}}\right)L_{3}L_{1}=-c_{0}n_{1}\\&C{\dot {\omega }}_{3}={\dot {L}}_{3}=0\end{aligned}}}$

${\displaystyle {\begin{aligned}{\dot {n}}_{1}=&\omega _{3}n_{2}-\omega _{2}n_{3}={\frac {L_{3}}{C}}n_{2}-{\frac {L_{2}}{A}}n_{3}\\{\dot {n}}_{2}=&\omega _{1}n_{3}-\omega _{3}n_{1}={\frac {L_{1}}{A}}n_{3}-{\frac {L_{3}}{C}}n_{1}\\{\dot {n}}_{3}=&\omega _{2}n_{1}-\omega _{1}n_{2}={\frac {L_{2}}{A}}n_{1}-{\frac {L_{1}}{A}}n_{2}\end{aligned}}}$

an. Der Überpunkt bildet die Zeitableitung, c₀ = mg s das Stützpunktmoment resultierend aus der Gewichtskraft mg und dem Abstand s des Schwerpunkts vom Stützpunkt auf der Figurenachse und für j = 1,2,3 ist jeweils

• ω_j die Komponente der Winkelgeschwindigkeit,
• L_j die Komponente des Drehimpulses und
• n_j die Komponente des Einheitsvektors ê_z

im Hauptachsensystem.

Unter Verwendung der Euler-Winkel sind die letzten drei Poisson-Gleichungen identisch erfüllt und die ersten drei Euler-Gleichungen spezialisieren sich zu

${\displaystyle {\begin{aligned}c_{0}\sin(\vartheta )\cos(\varphi )=&A{\dot {\omega }}_{1}+(C-A)\omega _{2}\omega _{3}\\-c_{0}\sin(\vartheta )\sin(\varphi )=&A{\dot {\omega }}_{2}+(A-C)\omega _{3}\omega _{1}\\0=&C{\dot {\omega }}_{3}\end{aligned}}}$

Einsetzen der Winkelgeschwindigkeiten

${\displaystyle {\begin{aligned}\omega _{1}=&{\dot {\psi }}\sin(\vartheta )\sin(\varphi )+{\dot {\vartheta }}\cos(\varphi )\\\omega _{2}=&{\dot {\psi }}\sin(\vartheta )\cos(\varphi )-{\dot {\vartheta }}\sin(\varphi )\\\omega _{3}=&{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}\end{aligned}}}$

und deren Zeitableitungen liefert Differentialgleichungen zweiter Ordnung in den Winkeln:[3]^:51

${\displaystyle {\begin{aligned}{\ddot {\psi }}=&{\frac {-2A{\dot {\psi }}\cos(\vartheta )+C({\dot {\varphi }}+{\dot {\psi }}\cos(\vartheta ))}{A\sin(\vartheta )}}{\dot {\vartheta }}={\frac {-2A{\dot {\psi }}\cos(\vartheta )+C\omega _{3}}{A\sin(\vartheta )}}{\dot {\vartheta }}\\{\ddot {\vartheta }}=&{\frac {(A-C){\dot {\psi }}^{2}\cos(\vartheta )-C{\dot {\psi }}{\dot {\varphi }}+c_{0}}{A}}\sin(\vartheta )={\frac {A{\dot {\psi }}^{2}\cos(\vartheta )-C\omega _{3}{\dot {\psi }}+c_{0}}{A}}\sin(\vartheta )\\{\ddot {\varphi }}=&{\dot {\psi }}{\dot {\vartheta }}\sin(\vartheta )-{\ddot {\psi }}\cos(\vartheta )\end{aligned}}}$

Die Winkelbeschleunigungen ${\displaystyle {\ddot {\psi }},{\ddot {\varphi }}}$ sind proportional zur Winkelgeschwindigkeit ${\displaystyle {\dot {\vartheta }}}$. Wo der Winkel ϑ momentan stillsteht – wie beispielsweise bei der regulären Präzession – bleiben die Winkelgeschwindigkeiten ${\displaystyle {\dot {\psi }},{\dot {\varphi }}}$ unveränderlich.

Abb. 9: Locuskurve (rot) mit ihrer senkrechten Projektion auf die horizontale Ebene (blau) beim aufrechten Kreisel

Bei einem Kreisel, der im oberen Totpunkt rotiert, ist L_z = L₃. Der aufrechte Kreisel dreht im oberen Totpunkt nur um die Figurenachse und die Kreiselfunktion vereinfacht sich zu

${\displaystyle {\dot {u}}^{2}=U(u)={\frac {2c_{0}}{A}}\left(u+{\frac {2Ac_{0}-L^{2}}{2Ac_{0}}}\right)(1-u)^{2}}$

Um den oberen Totpunkt u = 1 kann der Kreisel beständig rotieren. Wenn

L² > 4 A c₀

ist, dann ist unter realen Umständen U ≤ 0 und der Kreisel kann die Senkrechte u = 1 ohne äußere Einwirkungen nicht verlassen. Ein solcher Kreisel wird schlafender Kreisel genannt und seine Bewegung ist eine stabile.

Nach einer Weile kann der Drehimpuls infolge Reibung soweit abnehmen, dass L² < 4 A c₀ wird. Dann wird der obere Totpunkt eine instabile Gleichgewichtslage[1]^:109[3]^:123 und der Kreisel kann aus der Senkrechten ausbrechen. Bei einem geringfügigen Anstoß verlässt der Kreisel den oberen Totpunkt, fällt zum Breitenkreis mit ${\displaystyle u={\tfrac {L^{2}-2Ac_{0}}{2Ac_{0}}}=:{\textsf {e}}}$ ab und kehrt zurück. Für diese Bewegung zum Breitenkreis e und zurück zum Ausgangspunkt nahe dem oberen Totpunkt kann die Locuskurve analytisch berechnet werden:

${\displaystyle \psi =\arctan {\sqrt {\frac {u-{\textsf {e}}}{1+{\textsf {e}}}}}+{\frac {1}{2}}{\sqrt {\frac {1+{\textsf {e}}}{1-{\textsf {e}}}}}\ln {\frac {{\sqrt {1-{\textsf {e}}}}+{\sqrt {u-{\textsf {e}}}}}{{\sqrt {1-{\textsf {e}}}}-{\sqrt {u-{\textsf {e}}}}}}}$

Darin ist arctan der Arcus-Tangens und ln der natürliche Logarithmus. Die Kurve ist eine Art sphärische logarithmische Spirale die den Breitenkreis e tangiert und sich unendlich oft um den oberen Totpunkt windet, siehe Abb. 9.[1]^:107[3]^:124

Bei einem Kreisel, der um den unteren Totpunkt rotiert, ist L_z = -L₃ und die Kreiselfunktion vereinfacht sich zu

${\displaystyle {\dot {u}}^{2}=U(u)=-{\frac {1}{A^{2}}}[2Ac_{0}(1-u)+L^{2}](1+u)^{2}}$

Um den unteren Totpunkt u = -1 kann der Kreisel beständig rotieren. Weil jedoch U unter keinen realen Umständen positiv wird, kann der senkrecht nach unten hängende, rotierende Lagrange-Kreisel die Lotlinie ohne äußere Einwirkungen nicht verlassen. Der untere Totpunkt ist eine jedenfalls stabile Gleichgewichtslage[1]^:110.

Das ist im Gegensatz zum gleichmäßig rotierenden gestreckten Fliehkraftpendel, bei dem der untere Totpunkt bei einer kritischen Drehzahl instabil wird. Dort wird jedoch die Winkelgeschwindigkeit um die Lotlinie künstlich konstant gehalten, was beim sich selbst überlassenen Lagrange-Kreisel nicht der Fall ist. Dem Pendel wird, sobald es minimal von der Lotlinie abweicht, unablässig Drehimpuls zugeführt, bis eine Position gefunden ist, in der das Moment der Fliehkraft mit dem Moment der Gewichtskraft im Gleichgewicht ist.[1]^:111

Die Reibung in den Drehlagern der Aufhängung bewirken folgendes:

• Bei pseudoregulärer Präzession werden die Nutationen kleiner und verschwinden schließlich, sodass die Bewegung in eine reguläre Präzession übergeht.
• Der axiale Drehimpuls nimmt beständig ab.
• Die Präzessionsgeschwindigkeit wächst, denn sie ist umgekehrt proportional zum axialen Drehimpuls.
• Der Neigungswinkel ϑ nimmt zu, sodass sich die Figurenachse absenkt.
• Die Kreiselbewegung kommt irgendwann zum Stillstand.

Wenn der Drehimpuls so weit abnimmt, dass der Kreisel aufhört ein schneller zu sein, noch ehe die Figurenachse merklich abwärts weist, so wird die Wirkung der Reibung verwickelter.

Diesem Fall liegt die Annahme zugrunde, dass die Figurenachse im Stützpunkt in einer Halbkugel ausläuft, die sich in der Spitze eines nach oben offenen Kegeltrichters befindet und durch die Gewichtskraft dort festgehalten wird. Der Stützpunkt befindet sich hier im Mittelpunkt der Halbkugel, die bei der Drehung des Kreisels im Kegel mit Schlupf gleitet. Die Reibkraft wirkt etwa senkrecht zur Präzessionsebene in horizontaler Richtung und entgegengesetzt zur Tangentialgeschwindigkeit der Berührungspunkte auf der Halbkugel. Entsprechend übt die Reibkraft ein Drehmoment aus, das in der Präzessionsebene etwa waagerecht orientiert ist und mit der Figurenachse einen stumpfen Winkel einschließt. Dieses Reibmoment besitzt eine axiale und eine äquatoriale Komponente bezüglich des Kreisels. Die axiale Komponente vermindert unablässig den axialen Drehimpuls, wodurch dann wieder die Präzessionsgeschwindigkeit zunimmt. Die äquatoriale Komponente in der Präzessionsebene hebt oder senkt die Figurenachse, je nachdem der Schwerpunkt des Kreisels höher oder tiefer als der Stützpunkt liegt. Wenn sie, wie üblich, höher liegt, dann nähert sich die Kreiselspitze in einer archimedischen Spirale in der Zeit ${\displaystyle t={\tfrac {L_{3}}{c_{0}}}\sin \vartheta }$ der Lotlinie. Anders als bei der kardanischen Aufhängung richtet sich hier der Kreisel auf.