Komplexität von Handschriften
Eine Ermittlung der Komplexität von Handschriften mit Hilfe einer Anzahl abzählbarer Parameter erlaubt eine a-priori-Einschätzung der Befundergiebigkeit bei schriftvergleichenden Untersuchungen zur Echtheit oder der Urheberidentität handgeschriebener Schriften.
A priori-Kriterien
Es ist anzumerken, dass neben der Komplexität auch weitere Kriterien wie Umfang und Vielfalt, Eigenprägung und Variabilität sowie die Zeitnähe des Vergleichsschriftmaterials zu den fraglichen Schreibleistungen erste Hinweise darauf liefern können, ob die dem Endergebnis zugrundeliegende Wahrscheinlichkeitsskala nach oben eingeschränkt werden muss oder ob sie uneingeschränkt ausgeschöpft werden kann. Das gutachtliche Ergebnis hängt in erster Linie von der Qualität, aber auch von der Quantität der Befunde ab: Je mehr hypothesenspezifisch wesentliche Befunde objektiviert werden können, desto valider wird das gutachtliche Ergebnis ausfallen.
Bislang wurde in forensischen Gutachten der Komplexität von Handschriften eher marginal Rechnung gezollt, indem diese lediglich einer "prima vista"-Einschätzung durch den Schriftsachverständigen unterzogen wurde. Eine hochwertigere Ausnutzung des Kriteriums "Komplexität" wird im Folgenden beschrieben.
Zusammenhang Komplexität vs. Validität
Die Befund-Ergiebigkeit ihrerseits hängt ab von der Komplexität k und der Länge L der zu untersuchenden Schreibleistungen. Mit der weiter unten definierten – von L unabhängigen – relativen Komplexität lässt sich ein Maß für die Befundergiebigkeit definieren als
- E = k * L.
Die Komplexität wird üblicherweise auf einer grobgerasterten Ordinalskala mit nur wenigen Stufen (sehr niedrig … mittel … sehr hoch) abgeschätzt. Schließt man hochgradig gestörte Schriften aus, darf davon ausgegangen werden, dass in erster Näherung die folgende Proportionalität besteht:
- E = k * L ~ Validität.
Der Gutachter kann nur selten dem eigentlichen Entstehungsprozess des Schriftzuges beim Schreibvorgang beiwohnen. In den meisten Fällen liegt das Schreibprodukt fertig vor. Demgemäß kann nur die rein formale Komplexität des fertigen Schriftzuges, nicht aber die Komplexität der zugrundeliegenden Steuerungsprozesse beobachtet werden (s. unten).
Parameter
Ähnlich wie bei der Strichspannung[1] kann bei der Einschätzung der Komplexität das Bild eines Seiles hilfreich sein, das mehr oder weniger geordnet abgelegt worden ist und dabei komplexere oder einfachere Muster bildet. Es mag gewunden sein, es mag Schleifen bilden, dabei in sich mehrfach überkreuz liegen, zerhackt und aus mehreren Teilstücken zusammengesetzt sein. – Analog hierzu bieten sich zur Beschreibung der Komplexität von Schriftzügen die im Folgenden näher beschriebenen Parameter an.
Strichkreuzungen
Unter einer Strichkreuzung S versteht man die berührende oder überlappende Überlagerung zweier im Ablauf eines Schriftzuges nacheinander gefertigter Teile des Striches in der Ebene des Schriftträgers.
Strichkreuzungen 1. Ordnung:  "echte" Strichkreuzung | 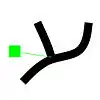 überlappende T-Formen |  berührende T-Formen |
Strichkreuzungen 2. Ordnung: 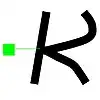 überlappende Bogenform |  berührende Bogenformen | Entstehung: Zwei Kreuzungspunkte 1. Ordnung fallen zu einem überlappenden bzw. berührenden Kreuzungspunkt zweiter Ordnung zusammen |
Strichkreuzungen höherer Ordnung:  Strichkreuzung höherer Ordnung: teildeckzügig | Veränderung der Krümmung (v. l. n. r.): Schlinge, Spitzkehre, Winkel, Bogen, Deckzug |
Bewegungsunterbrechungen
Unter einer Bewegungsunterbrechung U innerhalb eines Schriftzuges ist – unbeschadet etwaiger Strichüberlappungen/-berührungen – das Abheben des Schreibgerätes vom Schriftträger mit anschließender Neuaufnahme des Schreibvorgangs zu verstehen.
Beispiel-Muster:  zeichenintern: Nach dem 1. Grundstrich und nach der Querung wird das Schreibgerät abgehoben. | 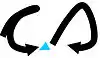 Unterbrechung zur Trennung zweier Zeichen |
Zwar sind kürzere Bewegungselemente der effektiv und affektiv eingesetzten Kontrolle des Schreibvorgangs leichter zugänglich. Aber es ist zu unterscheiden, ob der avisierte Schreibvorgang oder das fertige Schreibprodukt beurteilt werden soll. Die Aneinanderreihung kurzer Bewegungselemente mag leichter fallen, aber das formale Produkt selbst ist dennoch möglicherweise hoch komplex. (Man vergleiche eine Menge von kurzen Seilstücken, die kunstvoll so zusammengelegt werden, dass der Eindruck eines zusammenhängenden Gebildes entsteht.) Insofern sind erkennbare Bewegungsunterbrechungen bei der Ermittlung der Komplexität eines Schriftzuges – trotz erleichterter Kontrolle während des Schreibvorgangs – ebenfalls abzuzählen.
Wendepunkte
Unter einem Wendepunkt W versteht man den Ort eines Drehrichtungswechsels ein und desselben Schriftzuges in der Ebene des Schriftträgers von der Bewegungsrichtung im Uhrzeigersinn zur Bewegungsrichtung gegen den Uhrzeigersinn und umgekehrt.
Beispiel-Muster(1):  Wendepunkt 1. Ordnung: S-Form: Anfangsspin gegen den Uhrzeigersinn, Endspin im Uhrzeigersinn drehend | ||
Wendepunkte 2. und höherer Ordnung:  Winkel |  Spitzkehre(2) |  Deckzug |
| Entstehung von Wendepunkten höherer Ordnung: Die beiden ursprünglichen Wendepunkte erster Ordnung rücken zusammen und verschmelzen im Knotenpunkt des Winkels. Nach Erweiterung zur Schleife entfällt der Wendepunkt. | ||
Wendepunkte bei Bewegungsunterbrechungen:  Bewegungsunterbrechung mit Spinwechsel = 1 Wendepunkt |  Bewegungsunterbrechung ohne Spinwechsel = kein Wendepunkt |  Bewegungsunterbrechung zwischen bogen- und linienzügigen Elementen = 1 Wendepunkt |
- (1) Feinheiten der Strichbeschaffenheit (wie z. B. der Bewegungsvor- und -rückschläge, Tremor …) werden nicht berücksichtigt.
- (2) Im Gegensatz zu den beiden Schenkeln eines Winkels gehen die „Schenkel“ der Spitzkehre im Knotenpunkt tangential in die gleiche Richtung über.
Besonderheiten
Die Komplexität mancher Sonderformen F werden durch die zuvor angegebenen Parameter nur unbefriedigend beschrieben. Sonderformen können zusätzlich gezählt werden.
Ausrollungen:  1 Zähler | 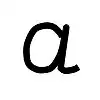 Das "a" ist geringer komplex als das "at" | ||
Einrollungen:  2 Zähler (1/Windung) |  Die "6" ist geringer komplex als die Einrollung | ||
Sonstige:  Bewegungsrückführungen |  Bewegungsrückführung | zusätzlich: z. B. Unterstreichungen, Verlängerungen etc. |
Bei Querungen ergeben die zusätzlichen Kreuzungen eine unzulässige Erhöhung der Komplexität, wie das folgende Beispiel zeigt:
kreuzende Querungen:  unzulässige Erhöhung um die Anzahl der Strichkreuzungen |
Die zusätzlichen Kreuzungen werden nicht gezählt, stattdessen gilt nur die Zahl der Querungen:
Äquivalent:  Die 7 Kreuzungen werden durch 1 Querung ersetzt |
Praxisbeispiele
In den folgenden Beispielen sind für die Parameter
 |
die Kennzeichnungen „von Hand“ gesetzt.
Beispiel 1: Unterschrift „N. Volkhausen“
Schriftsystem: Lateinisches Ausgangsalphabet; Schriftart: Anlehnung an Kurrentschrift


(1) Normschriftzug: Bei den Strichkreuzungen 2 (im „k“) und 4 (im „h“) handelt es sich um „echte“ Strichkreuzungen mit dem unmittelbar nachfolgenden Grundstrich. Die Strichkreuzungen 3 und 5 rühren von der Deckzügigkeit des Anstrichs mit dem zweiten Aufstrich der Buchstaben her.
Beispiel 2: Unterschrift „Kamahn“
Schriftsystem: Lateinisches Ausgangsalphabet; Schriftart: Anlehnung an Druckschrift



- (1) Normschriftzug: Kein Spinwechsel zwischen Linienzügen (z. B. „h“ – „n“. Je nach Druckschrift-Set variieren einige Zeichenformen erheblich. (z. B. die „a“-Form; s. Absatz „Kritik“.
Rechnerische Ermittlung der Komplexität
Die oben genannten Parameter sind in den meisten Fällen abzählbar und führen zu einem rechnerischen Zugang der Beschreibung der Komplexität von Schriftgebilden. Mit geringem Zähl- und Zeitaufwand lässt sich vor jeder schriftvergleichenden Untersuchung ein Zahlenwert ermitteln, der die Komplexität des zu untersuchenden Objektes hinreichend genau widerspiegelt.
Es wird vorgeschlagen, die absolute Komplexität der Schriftzüge als Summe aus den obigen Parametern zu ermitteln.
| Beispiel 1 | Beispiel 2 | |
|---|---|---|
| eigengeprägter Schriftzug: | K1e = W+U+S+F = 13+3+6+0 = 22 | K2e = W+U+S+F = 7+6+8+0 = 21 |
| Normschriftzug: | K1n = W+U+S+F = 26+4+7+0 = 37 | K2n = W+U+S+F = 8+13+10+0 = 31 |
| relative Komplexität: | k1 = 22/37 ≈ 0,59 | k2 = 21/31 ≈ 0,68 |
Man sieht: Die Länge des untersuchten Schriftzuges spielt wegen der Normierung keine Rolle.
Bei Textschriften wird die Ermittlung etwa von drei „schrifttypischen“ Worten (Anfang – Mitte – Ende) empfohlen. Wenn nicht nur von der jeweiligen fraglichen, sondern auch von einer Vergleichsschrift die Komplexität ermittelt wird, erhält man neben den üblichen Befunden noch einen weiteren auswertbaren Vergleichsbefund.
In größeren Schreiberpopulationen lassen sich über der Menge vieler Schriftzüge
- Mittelwert km und Standardabweichung SA
der jeweiligen relativen Komplexitäten getrennt für Unterschriften und Textschriften in Abhängigkeit vom Schriftsystem (Lateinisches Alphabet/Sütterlin/…) und von der Schriftart (Kurrent-/Druck-/Blockschrift) berechnen (s. u.). In jedem Fall lässt sich eine
- Normalkomplexität als kn := 1
definieren, bei der der untersuchte Schriftzug die gleiche absolute Komplexität wie der hierzu zeichenweise übereinstimmende Normschriftzug hat.
Skalenniveau
Ein Übergang von den Zahlenwerten der Proportionalskala auf eine Ordinalskala der Art:
- sehr große Komplexität
- große
- eher große
- mittlere Komplexität
- eher kleine
- kleine
- sehr kleine Komplexität
ist wünschenswert: Einerseits steht die Begrifflichkeit der Ordinalskala dem Verständnis der Alltagssprache näher als reine Zahlenwerte, andererseits beruht der Zahlenwert der relativen Komplexität auf einer genauen und nachvollziehbaren Ermittlung durch Abzählung der Parameter. Allerdings sollten sowohl der Zahlenwert für die relative Komplexität als auch der Rang der obigen Skala nebeneinander genannt werden, damit der Begriff der „Komplexität“ von Laien (Rechtsanwälten, Richtern, Beteiligten) leicht verstanden und akzeptiert wird.
Kritik
Verteilung
Dem steht jedoch entgegen, dass in größeren Schreiberpopulationen keine Normalverteilung (Gauß-Kurve der relativen Komplexität) zu erwarten ist, sondern eine zum Mittelwert km asymmetrische Verteilungskurve, die zudem noch gegen Null begrenzt ist. Die relativen Komplexitäten können nämlich theoretisch aus dem Intervall stammen.
Ein Übergang von der Proportionalskala der Zahlenwerte zur obigen siebenstufigen bipolaren Ordinalskala ist dadurch möglich, dass das Intervall zwischen k = 0 (minimale Komplexität) und k = km (Mittelwert der Komplexitäten) in sieben gleich große Intervalle geteilt und den unteren Komplexitätsgraden in der folgenden Art zugeordnet wird:
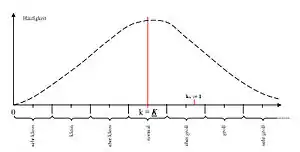
Eine Spiegelung um die Vertikale durch k = k führt auf die höheren Komplexitätsintervalle.
Axiomatik
Jedem der Parameter Strichkreuzungen, Wendepunkte, Bewegungsunterbrechungen und Einzelformen den Zählwert eins beizumessen, muss in Ermangelung einer angemessenen Gewichtung willkürlich bleiben. Auch die Summenbildung über alle Zähler der genannten Parameter ist nicht axiomatisch verankert. Es handelt sich lediglich um praktisch anwendbare Definitionen bzw. Vorgehensweisen, die ihre Gültigkeit aus einer wirklichkeitsnahen Wiedergabe der Gegebenheiten gewinnen, wie sie sich für den Schriftsachverständigen bei der Anschauung eines mehr oder weniger komplexen Schriftgebildes im Vergleich mit den Vorgaben der Schulnorm durch Abschätzung erschließen. Demgemäß ist der hier dargestellte Begriff der relativen Komplexität eines Schriftgebildes plausibel und praktikabel, aber verhandelbar. Die hier vorgeschlagene Systematik kann durch jede andere ersetzt werden, sofern sich in Fachkreisen ein besserer Konsens findet.
Druckschriften-Set
Bei druckschriftlichen Erzeugnissen kann die Normschrift trotz gegebenem Schriftsystem/Schriftart (verschiedene Sets!) stark variieren. Beispielsweise variiert das lateinische Kürzel für „et“ je nach künstlerischer Ausgestaltung in der folgenden Weise:
-Varianten.jpg.webp)
Außerdem hängt die Anzahl der Wendepunkte u. U. davon ab, wie die handschriftliche Reproduktion des druckschriftlichen Bildes imaginiert und vollzogen wird.
Es wird vorgeschlagen, der Normung eine der aktuell am häufigsten verwendeten serifenlosen Schriftarten zugrunde zu legen, beispielsweise Arial.
Literatur
- J. C. Sita, D. Rogers, B. Found: A Model Using Complexity Classification, Spatial Score and Line Quality for Forensic Signature Comparison. Teulings, H.L. u. van Gemmert; A.W.A. (Hrsg.): Proceedings of the 11th Conference of the International Graphonomics Society (IGS); Scottsdale 2003. 257-260
- T. Dewhurst, B. Found, D. ROGERS: The Relationship Between Quantitatively Modelled Signature Complexity Levels and Forensic Document Examiners' Qualitative Opinions on Casework. Journal of Forensic Document Examination; 2007; 18; 21-40
- B. Schwid: Complexity of Writing Rated and Forged by Non-handwriting Experts. Ref. anl. 8. Biennial Conference of the International Graphonomics Society (IGS); Genua 1997. 119
- L. Michel: Leserlichkeit und Fälschungsresistenz von Unterschriften. Ref. anl. der Tagung der Gesellschaft für Forensische Schriftuntersuchung (GFS) in Dresden; 1996. Dresden 1996.
- D.D. Kerrick, A.C. Bovik: Microprocessor-Based Recognition of Handprinted Characters from a Tablet Input. Pattern Recognition; 1988; 21; 525-537
- J.E. Behrendt: Problems Associated with the Writing of Senile Dementia Patients; Ref. anl. 40. Annual Conference of ASQDE; Boston, Mass. 1982
Einzelnachweise
- Strichspannung - Die Strichspannung als Befundkategorie der Grundkomponente "Strichbeschaffenheit" bei der schriftvergleichenden Untersuchung.