Kerbgrundkonzept

Bild 1: Dehnungswöhlerlinie (schematisch) mit zugehörigen Parametern

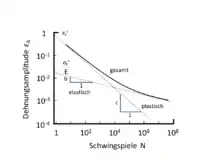
Die Basis zur Beschreibung der Widerstandsfähigkeit des Werkstoffes bildet die Dehnungswöhlerlinie (Bild 1: Dehnungswöhlerlinie).

Ermittelt wird diese mit einer polierten Probe in einem dehnungskontrollierten Versuch, bei konstantem Mittelspannungsverhältnis, normalerweise ${\displaystyle R_{\varepsilon }=-1}$, d. h. mittelspannungsfrei. Die Beziehung zwischen der Dehnungsamplitude und der Schwingspielzahl kann nach Manson[5], Coffin[6] und Morrow[7], für ein bestimmtes Mittelspannungsverhältnis, in der folgenden Form ausgedrückt werden:[4]

${\displaystyle \varepsilon _{A}=\varepsilon _{A,{\text{el}}}+\varepsilon _{A,{\text{pl}}}={\frac {\sigma _{f}^{'}}{E}}\cdot (2N)^{b}+\varepsilon _{f}^{'}\cdot (2N)^{c}}$

mit

${\displaystyle \varepsilon _{A}}$ – Dehnungsamplitude,

${\displaystyle N}$ – Schwingspiele (${\displaystyle N}$ Schwingspiele = ${\displaystyle 2N}$ Schwingumkehrungen),

${\displaystyle \sigma _{f}^{'}}$ – Schwingfestigkeitskoeffizient,

${\displaystyle b}$ – Schwingfestigkeitsexponent,

${\displaystyle \varepsilon _{f}^{'}}$ – zyklischer Duktilitätskoeffizient,

${\displaystyle c}$ – zyklischer Duktilitätsexponent,

${\displaystyle E}$ – Elastizitätsmodul.

Bild 2: Spannungs-Dehnungs-Hysteresen mit zugehöriger Last-Zeit-Folge, „Rechenbeispiel Kerbgrundkonzept“

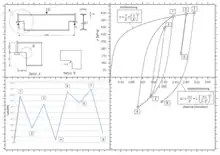
Zur Ermittlung der über-elastischen Spannungen bzw. Dehnungen im Kerbgrund wird ein (zyklisch stabilisiertes) Werkstoffgesetz benötigt. Versuchstechnisch wird die zyklische Werkstofffließkurve punktweise aus dem dehnungskontrollierten Wöhlerlinien-Versuch gewonnen. Um die zyklische Spannungs-Dehnungs-Kurve schneller und weniger aufwendig als punktweise durch dehnungskontrollierte Wöhler-Versuche zu bestimmen, gibt es den Incremental-Step-Test,[8] bei dem die Dehnungsamplitude stufenweise bis zu einem festzulegenden Größtwert gesteigert und stufenweise wieder vermindert wird. Dabei vollziehen sich etwaige Ver- oder Entfestigungen des Werkstoffs in ähnlicher, aber nicht unbedingt gleicher Weise wie im Wöhler-Versuch. Nach zwei oder drei Auf-Ab-Folgen dieser Art liefern die Umkehrpunkte der Beanspruchung eine weitgehend stabilisierte zyklische Spannungs-Dehnungs-Kurve, die sich in etwa mit derjenigen deckt, die sich aus Wöhler-Versuchen ergibt.[4] Zur analytischen Beschreibung der Werkstofffließkurve kann z. B. der Ansatz von Ramberg und Osgood herangezogen werden. Als Resultat ergeben sich, für beliebige Last-Zeit-Folgen, Spannungs-Dehnungs-Hysteresen mit entsprechenden offenen und geschlossenen Hystereseästen in einem ${\displaystyle \sigma }$-${\displaystyle \varepsilon }$-Diagramm (Bild 2: Spannungs-Dehnungs-Hysteresen). Die zyklisch stabilisierte ${\displaystyle \sigma }$-${\displaystyle \varepsilon }$-Kurve wird (für die Erstbelastung) wie folgt geschrieben:[9]

Bild 3: „Universal Material Law“ (UML) nach Bäumel und Seeger

${\displaystyle \varepsilon =\varepsilon _{\text{el}}+\varepsilon _{\text{pl}}={\frac {\sigma }{E}}+\left({\frac {\sigma }{K^{'}}}\right)^{1/n'}}$,

wobei ${\displaystyle K^{'}}$ den zyklischen Verfestigungskoeffizient und ${\displaystyle n'}$ den zyklischen Verfestigungsexponent darstellen. Zwischen der Werkstofffließkurve und der Dehnungswöhlerlinie gelten außerdem die Beziehungen (Kompatibilitätsbeziehung):

${\displaystyle K^{'}={\frac {\sigma _{f}^{'}}{(\varepsilon _{f})^{n'}}}}$

${\displaystyle n'={\frac {b}{c}}}$

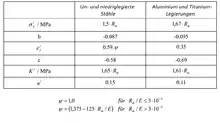
Eine Möglichkeit zyklische Werkstoffkennwerte, für un- und niedriglegierte Stähle sowie für Aluminium- und Titanium-Legierungen, abzuschätzen, bietet das „Universal Material Law“ (UML) von Bäumel und Seeger (Bild 3: Universal Material Law)[10]

Bei einer zyklischen Belastung von technischen Bauteilen (d. h. mehrfache Wiederbelastung) müssen zwei weitere Effekte berücksichtigt werden: das sogenannte Masing-Verhalten[11] und die Memory-Gesetze (oder auch Memory-Effekte). Masing-Verhalten bedeutet, dass bei Wiederbelastung eine Spannungs- bzw. Dehnungsschwingbreite ${\displaystyle (\Delta \sigma }$, ${\displaystyle \Delta \varepsilon )}$ angesetzt wird, die dem doppelten Amplitudenwert der Spannung bzw. Dehnung der Erstbelastungskurve entspricht (Bild 4: Drei verschiedene Formen der „Werkstoffgedächtnisse“):

${\displaystyle \Delta \sigma =2\cdot \sigma }$, ${\displaystyle \Delta \varepsilon =2\cdot \varepsilon }$.

Unter Berücksichtigung des Masing-Verhaltens ergibt sich somit für die Werkstofffließkurve nach Ramberg und Osgood bei Wiederbelastung:

${\displaystyle \Delta \varepsilon ={\frac {\Delta \sigma }{E}}+2\cdot \left({\frac {\Delta \sigma }{2\cdot K^{'}}}\right)^{1/n'}}$.

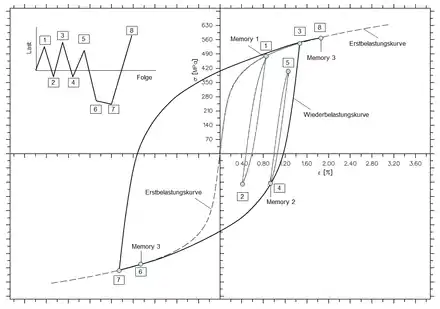
Bei den Memory-Gesetzen (Memory-Effekten) handelt es sich um eine Art Werkstoffgedächtnis. Nach[12][13] können drei verschiedene Formen von Memory-Gesetzen unterschieden werden (Memory 1 bis Memory 3, siehe Bild unten). Die folgende Beschreibung der Memory-Effekte wurde[4] entnommen:

• Für die Erstbelastung gilt die Spannungs-Dehnungs-Kurve als Spannungs-Dehnungs-Pfad (zyklisch stabilisierte ${\displaystyle \sigma }$-${\displaystyle \varepsilon }$-Kurve bzw. Erstbelastungskurve, Pfad 0–1).
• Memory 1: Nach dem Schließen einer Hystereseschleife (Wiederbelastungskurve unter Berücksichtigung des Masing-Verhaltens, ${\displaystyle \Delta \sigma }$-${\displaystyle \Delta \varepsilon }$-Kurve), die auf der Erstbelastungskurve begonnen wurde (Pfad 1-2-1), verläuft der Spannungs-Dehnungs-Pfad weiter auf der Erstbelastungskurve (Pfad 1–3).
• Memory 2: Nach Schließen einer Hystereseschleife, die auf einem Schleifenast begonnen wurde (Pfad 4-5-4), folgt der Spannungs-Dehnungs-Pfad dem ursprünglichen Schleifenast (Pfad 3-4-6).
• Memory 3: Ein auf der Erstbelastungskurve begonnener Hysterese-Schleifenast (Pfad 3-4-6) endet, wenn der Spiegelpunkt 6 seines Startpunktes 3 im gegenüberliegenden Quadranten erreicht ist; sodann setzt sich der Spannungs-Dehnungs-Pfad auf der Erstbelastungskurve fort (Pfad 6–7).

Bild 4: Drei verschiedene Formen der „Werkstoffgedächtnisse“ nach[4]

Bild 5: Ermittlung der lokalen Spannungen und Dehnungen mittels der Neuber-Regel

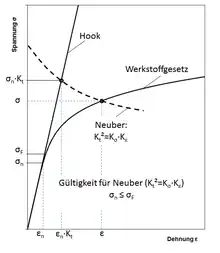
Der Zusammenhang zwischen der äußeren Belastung und der lokalen Spannung bzw. Dehnung, lässt sich nach der Kerbnäherungsbeziehung nach Neuber (Bild 5: Ermittlung der lokalen Spannungen), ausgehend von der Makrostützwirkungsformel, wie folgt herstellen.[14]

${\displaystyle K_{t}^{2}=K_{\varepsilon }\cdot K_{\sigma }}$ (Makrostützwirkungsformel),

dabei stellen ${\displaystyle K_{t}}$ die (elastizitäts-theoretische) Kerbformzahl, ${\displaystyle K_{\varepsilon }}$ und ${\displaystyle K_{\sigma }}$ die inelastischen Spannungs- bzw. Dehnungsformzahlen dar. Unter Berücksichtigung des Hookeschen Gesetzes ${\displaystyle (E={\frac {\sigma }{\varepsilon }})}$ sowie des Zusammenhangs zwischen örtlicher (inelastischer) Spannung bzw. Dehnung und Mechanische Spannung bzw. -dehnung (${\displaystyle K_{\varepsilon }={\frac {\varepsilon }{\varepsilon _{n}}},K_{\sigma }={\frac {\sigma }{\sigma _{n}}}}$) lässt sich die Neuber-Formel wie folgt schreiben:

${\displaystyle {\frac {K_{t}^{2}\cdot \sigma _{n}^{2}}{E}}=\varepsilon \cdot \sigma }$.

Soll wegen der Stützwirkung ${\displaystyle n}$ die Beanspruchung reduziert werden, kann statt der Kerbformzahl ${\displaystyle K_{t}}$ die Kerbwirkungszahl ${\displaystyle K_{f}}$ verwendet und dem oben beschriebenen Werkstoffgesetz gleichgesetzt werden:[1]

${\displaystyle {\frac {K_{f}^{2}\cdot \sigma _{n}^{2}}{E}}=\left({\frac {\sigma }{E}}+\left({\frac {\sigma }{K^{'}}}\right)^{1/n'}\right)\cdot \sigma }$ (Erstbelastung)

${\displaystyle {\frac {K_{f}^{2}\cdot \Delta \sigma _{n}^{2}}{E}}=\left({\frac {\Delta \sigma }{E}}+2\cdot \left({\frac {\Delta \sigma }{2\cdot K^{'}}}\right)^{1/n'}\right)\cdot \Delta \sigma }$ (Wiederbelastung, Masing-Verhalten)

Die Neuber-Regel gilt genaugenommen nur in dem Fall, wenn sich der Nettoquerschnitt rein elastisch verhält. Die elastisch-plastische Kerbbeanspruchung nach teilweiser oder vollständiger Plastifizierung des Nettoquerschnitts lässt sich nach Seeger und Heuler[15] über folgende Modifikation der Neuber-Formel bestimmen:[3][4]

${\displaystyle K_{t}^{2}\cdot {\frac {\varepsilon _{n}^{*}\cdot E}{\sigma _{n}^{*}}}=K_{\varepsilon }\cdot K_{\sigma }}$.

Dabei werden die traglastbezogene Nennspannung

${\displaystyle \sigma _{n}^{*}=\sigma _{n}\cdot {\frac {K_{t}}{K_{p}}}}$,

zusammen mit der gemäß Spannungs-Dehnungs-Kurve des Werkstoffs modifizierten Nenndehnung

${\displaystyle \varepsilon _{n}^{*}=f(\sigma _{n}^{*})}$

und die Traglastformzahl

${\displaystyle K_{p}={\frac {\sigma _{\text{pl}}}{\sigma _{n,F}}}}$

eingeführt. Die modifizierte Nenndehnung wird, bei Verwendung des Werkstoffgesetzes nach Ramberg und Osgood (siehe oben), wie folgt geschrieben:

${\displaystyle \varepsilon _{n}^{*}={\frac {\sigma _{n}^{*}}{E}}+\left({\frac {\sigma _{n}^{*}}{K^{'}}}\right)^{1/n'}}$

Mit den bisher besprochenen Berechnungsbausteinen (Masing-Verhalten, Werkstoffgedächtnis sowie die Kerbnäherungsbeziehung) lassen sich die Spannungs-Dehnungs-Pfade unter Berücksichtigung des Werkstoffverhaltens sowie der auf das Bauteil einwirkenden Last ermitteln. Liegt eine Einstufenlast vor, können die schädigungswirksamen Spannungs-Dehnungs-Hysteresen direkt mit der Dehnungswöhlerlinie verglichen werden. Dabei kann die Fläche innerhalb einer geschlossenen Hysterese, als ein Maß für die Werkstoffschädigung betrachtet werden. Im Falle einer Betriebslast, in der, zeitlich, eine beliebige Last-Zeit-Folge auf das Bauteil einwirkt, ist ein Vergleich der Hysteresen mit der Dehnungswöhlerlinie, welche für ein bestimmtes Lastverhältnis gilt, nicht mehr möglich. Hier müssen die Hysteresen bezüglich der Mittelspannung bzw. -dehnung transformiert, d. h., in schädigungsequivalente Hysteresen mit einer Mittelspannung von ${\displaystyle \sigma _{m}=0}$ umgerechnet werden. Dies erfolgt mit einem sogenannten Schädigungsparameter (oder auch Mittelspannungsparameter genannt), welcher diesem Sachverhalt, durch eine entsprechende Berücksichtigung in der Schadensakkumulation Rechnung trägt. Der in der Fachliteratur am weitesten verbreitete Parameter stammt von Smith, Watson und Topper[16]:

${\displaystyle P_{SWT}={\sqrt {(\sigma _{a}+\sigma _{m})\cdot \varepsilon _{a}\cdot E}}}$.

Dabei entsprechen ${\displaystyle \sigma _{a}}$, ${\displaystyle \varepsilon _{a}}$ bzw. ${\displaystyle \sigma _{m}}$ dem Amplituden- bzw. dem Mittelwert einer Spannungs-Dehnungs-Hysterese. Eine Schwäche des Schädigungsparameter P_SWT ist die, dass er bei Druckmittelspannungen (${\displaystyle \sigma _{m}<0}$) die ertragbaren Amplituden, insbesondere bei hochfesten Stählen, deutlich zu hoch vorher sagt.[17] Eine Übersicht über die verschiedenen Schädigungsparameter wird vor allem in[1][3][4][18] gegeben.

Auf der Seite der Beanspruchbarkeit muss die entsprechende Dehnungswöhlerlinie in eine dem Schädigungsparameter entsprechende Wöhlerlinie umgerechnet werden. Bei Verwendung des Ansatzes nach Manson, Coffin, Morrow (siehe oben) erhält man für die Mittelspannung ${\displaystyle \sigma _{m}=0}$ die P_SWT-Wöhlerline:

${\displaystyle P_{SWT}={\sqrt {\sigma _{f}^{'2}\cdot (2\cdot N)^{2b}+\sigma _{f}^{'}\cdot \varepsilon _{f}^{'}\cdot E\cdot (2\cdot N)^{b+c}}}}$.

Bei schwingender Beanspruchung wird die Kerbwirkung mittels der Kerbwirkungszahl ${\displaystyle K_{f}}$ im Festigkeitsnachweis berücksichtigt (wobei das Formelzeichen ${\displaystyle \beta _{k}}$ häufig verwendet wird). Der mögliche Wertebereich von ${\displaystyle K_{f}}$ ist dabei:

${\displaystyle 1\leq K_{f}\leq K_{t}}$

Erreicht die Kerbwirkungszahl betragsmäßig den Wert der (elastizitäts-theoretischen) Kerbformzahl ${\displaystyle K_{t}}$ (oder auch ${\displaystyle \alpha _{k}}$) ist die theoretisch errechnete Spannungsspitze voll schädigungswirksam; ist die Kerbwirkungszahl dagegen 1, bedeutet das, dass sich die Kerbe gegenüber einem ungekerbter Probestab, mit den Abmessungen des Kerbquerschnitts, nicht festigkeitsmindernd auswirkt.[19] Das Verhältnis zwischen theoretischer und schwingfestigkeitswirksamer Spannungsüberhöhung wird dabei mittels einer Stützziffer ausgedrückt:

${\displaystyle n={\frac {K_{t}}{K_{f}}}}$.

Bild 6: Spannungsgradientenansatz nach Siebel und Stiehler

Zur Bestimmung der Stützziffer existieren verschiedene Modelle; zwei sehr bekannte Modelle sind:

• das Verfahren nach Siebel und Stieler[20] (Spannungsgradientenansatz)
• sowie der Spannungsmittelungsansatz nach Neuber[21]

Für weiterführende Informationen siehe Grundlagen[19] oder weiterführende Fachliteratur.[3]

Die Berechnung der Stützziffer nach Siebel und Stieler – diese soll hier kurz angesprochen werden – beruht auf dem bezogenen Spannungsgradienten an der Stelle der höchsten Beanspruchung. Der auf die maximale elastische Kerbspannung bezogene Spannungsgradient ${\displaystyle \chi ^{*}}$ berechnet sich zu (Bild 6: Spannungsgradientenansatz):

${\displaystyle \chi ^{*}={\frac {1}{\sigma _{\text{max}}}}\left({\frac {d\sigma }{dx}}\right)_{x=0}}$.

Die Zuordnung zwischen dem bezogenen Spannungsgradienten ${\displaystyle \chi ^{*}}$ und der dynamischen Stützziffer ${\displaystyle n_{\chi ^{*}}}$ (der Buchstabe ${\displaystyle \chi ^{*}}$, im tiefgestellten Index, deutet an, dass die dynamische Stützziffer, siehe oben, nach dem Spannungsgradientenansatz ermittelt wurde) erfolgt werkstoffabhängig und kann Tabellenwerken[22] oder der Fachliteratur (z. B.[19][3]) entnommen werden:

${\displaystyle n_{\chi ^{*}}=f(\chi ^{*}}$, Werkstoff${\displaystyle )}$.

Die so ermittelte Stützziffer kann im Rahmen des Kerbdehnkonzeptes nicht unmittelbar angewendet werden. Diese muss zunächst aufgrund möglicher Anteile größerer plastischer Verformungen, welche auf der makroskopischen Stützwirkung (Abbau der Kerbwirkung durch lokales Fließen) beruhen, modifiziert werden. Ein Ansatz, der von Neuber stammt und in[17] beschrieben wird, resultiert in die Makrostützwirkung ${\displaystyle n_{p}}$:

${\displaystyle n_{p}={\sqrt {1+{\frac {\varepsilon _{D}^{\text{pl}}}{\varepsilon _{D}^{\text{el}}}}}}}$,

dabei sind ${\displaystyle \varepsilon _{D}^{\text{el}}}$ und ${\displaystyle \varepsilon _{D}^{\text{pl}}}$ die elastischen und plastischen Dehnungsanteile in der Dauerfestigkeit, die der Dehnungswöhlerlinie entnommen werden. Die bezüglich der Makrostützwirkung modifizierte Stützziffer ${\displaystyle n}$ ergibt sich damit zu:

${\displaystyle n={\frac {n_{p}}{n_{\chi ^{*}}}}}$.

Die Stützwirkung kann nun entweder auf der Seite der Beanspruchung, in der die Kerbwirkungszahl mittels der hier beschriebenen Stützziffer berechnet und zur Ermittlung der lokalen Spannungen und Dehnungen (siehe Abschnitt Kerbnäherungsbeziehung nach Neuber) herangezogen wird, oder alternativ, auf der Seite der Beanspruchbarkeit, durch das Anheben der ${\displaystyle P_{SWT}}$-Wöhlerlinie, berücksichtigt werden:

${\displaystyle P_{SWT,n}=n\cdot P_{SWT}}$

Grundsätzlich müssen alle signifikanten Faktoren und Einflüsse in die Lebensdauer-Berechnung einkalkuliert werden. In der Praxis sind das vor allem fertigungsbedingte Einflüsse, wie z. B. Eigenspannungen aus einer Oberflächenverfestigung, Oberflächenrauhigkeiten oder ein steiler Spannungsgradient bei scharfen Kerben.

Um z. B. den Einfluss von Oberflächenrauhigkeiten in die Berechnung einzubeziehen, bestehen mehrere Möglichkeiten. Zum einen kann die Dehnungswöhlerlinie an Proben mit entsprechend rauer Oberfläche ermittelt werden. Zum anderen kann die Schädigungsparameter-Wöhlerlinie über einen Oberflächenfaktor im Verhältnis der Dauerfestigkeiten bei rauer und polierter Oberfläche abgemindert werden. In beiden Fällen geht dabei i. d. R. summarisch neben dem Rauigkeitseinfluss auch noch der in anderer Weise zu bewertenden Einfluss etwaiger Eigenspannungen ein.[4] Siehe hierzu z. B. die FKM-Richtlinie.[22]

Bild 7: Lineare Schadensakkumulation

Auf Basis der berechneten Spannungs-Dehnungs-Hysteresen kann die Schädigungsrechnung durchgeführt werden. Dabei wird der Schädigungsbeitrag jeder einzelnen geschlossenen Spannungs-Dehnungs-Hysterese ${\displaystyle D_{j}}$ zu einer Schädigungssumme ${\displaystyle D}$ akkumuliert:

${\displaystyle D=\sum _{j=1}^{N_{i}}D_{j}=\sum _{j=1}^{N_{i}}{\frac {1}{N_{j}}}=1{,}0}$,

mit ${\displaystyle D=1{,}0}$ (Miner-Regel) oder einer anderen empirisch belegten Schädigungssumme (relative Miner-Regel). Siehe hierzu auch Bild 7 und den Artikel: Lineare Schadensakkumulation.