Halbwertszeit
Die Halbwertszeit oder Halbwertzeit[1] (abgekürzt HWZ, Formelzeichen meist , auch ) ist die Zeitspanne, nach der eine mit der Zeit abnehmende Größe die Hälfte des anfänglichen Werts (oder, in Medizin und Pharmakologie, die Hälfte des Höchstwertes) erreicht.
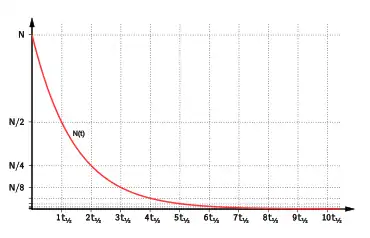
Folgt die Abnahme einem Exponentialgesetz (siehe Abbildung), dann ist die Halbwertszeit immer die gleiche, auch wenn man eine beliebige Zeitspanne abwartet und die Restmenge, die dann noch übrig ist, als neue Anfangsmenge nimmt. Bei einem Exponentialgesetz charakterisiert daher die Halbwertszeit den zugrunde liegenden Prozess als solchen.
Eine eng verwandte Größe ist die durchschnittliche Lebensdauer. Bei exponentieller Abnahme ist sie die Zeitspanne , nach der die Größe auf den Bruchteil 1/e ≈ 36,8 % des anfänglichen Wertes abgenommen hat.
Nimmt eine Größe dagegen mit der Zeit zu, so wird die Zeitspanne, nach der das Doppelte des anfänglichen Werts erreicht ist, als Verdopplungszeit bezeichnet. In der Mikrobiologie nennt man die Verdopplungszeit einer Population von Einzellern auch Generationszeit.
Halbwertszeiten in verschiedenen Vorgängen
Exponentielle Abnahme
Bei exponentieller Abnahme einer Größe hängt die Halbwertszeit weder von der Wahl des Anfangszeitpunkts noch von dem dann vorliegenden Startwert ab. In diesem Fall ist immer
- nach Verstreichen von der Wert auf ,
- nach auf ,
- nach auf ,
- allgemein nach auf
gefallen.
Radioaktive Zerfälle

Der radioaktive Zerfall eines gegebenen Radionuklids verläuft exponentiell. Die Halbwertszeit ist die Zeitspanne, in der die Menge und damit auch die Aktivität eines gegebenen Radionuklids durch den Zerfall auf die Hälfte gesunken ist.[2] 50 % der Atomkerne haben sich – i. A. unter Aussendung ionisierender Strahlung – in ein anderes Nuklid umgewandelt; dieses kann seinerseits ebenfalls radioaktiv sein oder nicht. Für jedes Nuklid ist die Halbwertszeit eine feste Größe, die sich nicht (nur in Ausnahmen ganz geringfügig) beeinflussen lässt.
Die Halbierung gilt allerdings nur als statistischer Mittelwert. Man findet sie umso genauer bestätigt, je mehr nicht zerfallene Atome die betrachtete Probe noch enthält. Der Zeitpunkt der Umwandlung eines einzelnen Atomkerns kann nicht vorhergesagt werden, nur die Wahrscheinlichkeit der Umwandlung pro Zeitintervall kann angegeben werden (Zerfallskonstante , siehe unten). Die Wahrscheinlichkeit, dass ein betrachteter einzelner Kern sich innerhalb der ersten Halbwertszeit umwandelt, beträgt 50 %, dass er sich innerhalb von zwei Halbwertszeiten umwandelt, 50 % + 25 % = 75 %, bei drei Halbwertszeiten 50 % + 25 % + 12,5 % = 87,5 % usw.
Es gibt radioaktive Halbwertszeiten im Bereich von weniger als einer Mikrosekunde bis zu einigen Quadrillionen Jahren. Polonium-212 beispielsweise hat 0,3 µs Halbwertszeit, Tellur-128 dagegen etwa 7·1024 (7 Quadrillionen) Jahre.
Eng verknüpft mit der Halbwertszeit eines Radionuklids ist seine spezifische Aktivität, also die Aktivität pro Masse, ausgedrückt z. B. in Becquerel pro Milligramm, Bq/mg. Der Zusammenhang zwischen spezifischer Aktivität und der Halbwertszeit ist umgekehrt proportional: je kürzer die Halbwertszeit, desto größer ist bei gegebener Substanzmenge die Aktivität und umgekehrt.
Die folgende Tabelle enthält einige Beispiele. In den Zahlenwerten ist hier nur die Masse des Radionuklids selbst berücksichtigt; in der Praxis werden spezifische Aktivitäten eher auf das jeweilige natürliche Isotopengemisch oder das Gesamtmaterial der Probe bezogen.
| Isotop | Halbwertszeit | spezifische Aktivität |
|---|---|---|
| 131I | 8 Tage | 4.600.000.000.000 Bq/mg |
| 3H | 12,33 Jahre | 370.000.000.000 Bq/mg |
| 137Cs | 30 Jahre | 3.300.000.000 Bq/mg |
| 239Pu | 24.110 Jahre | 2.307.900 Bq/mg |
| 235U | 703.800.000 Jahre | 80 Bq/mg |
| 238U | 4.468.000.000 Jahre | 12 Bq/mg |
| 232Th | 14.050.000.000 Jahre | 4 Bq/mg |
Erst Ende des 20. Jahrhunderts sind einige früher als stabil geltende Nuklide als extrem langlebige Radionuklide „entlarvt“ worden, zum Beispiel 149Sm, 152Gd (beides Lanthanoide), 174Hf, 180W und 209Bi mit Halbwertszeiten von bis zu einigen Trillionen Jahren. Die Aktivität ist bei so langen Halbwertszeiten entsprechend gering und nur mit großem Aufwand nachweisbar.
Für manche praktischen Zwecke, etwa bei der Betrachtung des gesamten Radioaktivitätsinventars eines Labors oder einer kerntechnischen Anlage, sieht man als Faustregel die Aktivität einer gegebenen Strahlenquelle nach 10 Halbwertszeiten als vernachlässigbar an, denn sie hat dann auf das 2−10-Fache (= 1/1024), also weniger als ein Tausendstel des Anfangswertes abgenommen.
Messung radioaktiver Halbwertszeiten
Zur Messung der Halbwertszeit sind wegen der verschiedenen Größenordnungen verschiedene Methoden nötig.
- In einem mittleren Bereich, für Halbwertszeiten etwa von Sekunden bis zu Tagen, kann man direkt die Abnahme bis auf die halbe Aktivität verfolgen.
- Sehr lange Halbwertszeiten misst man durch Zählen der Zerfälle pro Zeitintervall an einer bekannten Menge der Substanz; man bestimmt also nicht , sondern die Zerfallskonstante (siehe unten). Die genaue Menge des Radionuklids kann beispielsweise mittels Massenspektroskopie bestimmt werden. Mit einer solchen Methode ist die Halbwertszeit des Eisenisotops Fe-60 von 2,5·106 Jahren auf 2 % genau gemessen worden.[3]
- Für sehr kurze Halbwertszeiten gibt es Techniken, die z. B. den Ort des Zerfalls feststellen, wenn das Atom oder Molekül mit bekannter Geschwindigkeit an einer Reihe von Detektoren vorbeifliegt, und andere Methoden.[4]
- Extrem kurze Halbwertszeiten, z. B. von angeregten Kernzuständen im Bereich 10−22 … 10−16 Sekunden, kann man über die Zerfallsbreite der entstehenden Strahlung messen.
Datensammlungen
Die Halbwertszeiten aller Radionuklide sind in der Liste der Isotope zu finden. Allgemein werden sie neben weiteren Daten in Nuklidkarten angegeben. Eine sehr viel verwendete gedruckte Sammlung ist die Karlsruher Nuklidkarte.[5] Als Online-Nuklidkarte ist beispielsweise eine Darstellung vom Korean Atomic Energy Research Institute verfügbar.[6]
Geschichte
Die erste Beobachtung, dass die Aktivität eines Radionuklids in gleichen Zeiträumen um den gleichen Faktor abnimmt – also durch eine feststehende Halbwertszeit beschrieben werden kann – wurde 1900 von Rutherford veröffentlicht.[7][8] Die von Rutherford untersuchte Substanz war in heutiger Bezeichnungsweise das Radon-Isotop .
Biologische Halbwertszeit
Die biologische Halbwertszeit oder Eliminationshalbwertszeit (siehe auch Plasmahalbwertszeit) ist die Zeitspanne, in der in einem Organismus (Mensch, Tier, Pflanze, Einzeller) die Menge einer inkorporierten Substanz durch die Wirkung aller beteiligten biologischen Prozesse (Stoffwechsel, Ausscheidung usw.) auf die Hälfte abgesunken ist.[9][2]
In der Pharmakokinetik ist Halbwertszeit die Zeit, in der die Hälfte des aufgenommenen Arzneimittels verstoffwechselt oder ausgeschieden ist. Pharmakokinetische Halbwertszeiten können sehr verschieden sein. Beim Erwachsenen werden beispielsweise für Penicillin-G 0,5 Stunden angegeben, für Phenobarbital 120 Stunden.[10] Da an der Mengenabnahme verschiedene Prozesse mit teilweise verschiedenen Konzentrationsabhängigkeiten beteiligt sind, hängt die Eliminationshalbwertszeit mancher Stoffe von der Ausgangskonzentration ab; für Phenytoin beträgt sie z. B. bei geringer Konzentration sieben Stunden, bei höherer bis zu 40 Stunden.[10]
Effektive Halbwertszeit
Die effektive Halbwertszeit eines Radionuklids ist die Zeitspanne, innerhalb derer die halbe Menge eines inkorporierten (in einen Organismus aufgenommenen) Radionuklids verschwindet. Hier sind zwei Prozesse beteiligt, der radioaktive Zerfall und unabhängig davon die Wiederausscheidung durch den Stoffwechsel.[2] Beide verlaufen exponentiell mit meist unterschiedlichen Halbwertszeiten. Die resultierende Funktion kann durch eine einzige Exponentialfunktion und damit ebenfalls durch eine Halbwertszeit beschrieben werden.
Die effektive Halbwertszeit ist immer kleiner als die kleinere der beiden einzelnen Halbwertszeiten. Sind die biologische und die physikalische Halbwertszeit sehr verschieden, so entspricht die effektive Halbwertszeit etwa der kürzeren. Bei gleich langen Halbwertszeiten ist die effektive Halbwertszeit die Hälfte jeder der ursprünglichen Halbwertszeiten.
Bibliometrische Halbwertszeiten
In der Bibliometrie ist für das Veralten naturwissenschaftlicher Publikationen – gemessen an der abnehmenden Häufigkeit der Zitate in anderen Publikationen – ein mehr oder weniger exponentielles Verhalten mit einer Halbwertszeit von rund fünf Jahren festgestellt worden.[11] Aus der Benutzungsstatistik der Universitätsbibliothek Ulm wurde die gleiche Halbwertszeit auch für die Häufigkeit der Bestellungen von Kopien der Zeitschriftenartikel gefunden.[12] Eine naturwissenschaftliche Veröffentlichung wird also durchschnittlich jedes Jahr um etwa 13 % weniger oft gelesen oder zitiert als im vorangegangenen (abgesehen von Klassikern und den neuesten Werken).
Mathematische Definition
Vorbemerkung:
Das Zerfallsgesetz setzt als „Menge“ eine kontinuierliche, als reelle Zahl darstellbare Größe voraus. Es ist aber auch auf ganzzahlige Größen wie z. B. die Anzahl der Atome in der radioaktiven Substanzprobe anwendbar, denn es beschreibt jeweils den messtechnischen Erwartungswert, also Mittelwert über viele (gedachte) Einzelmessungen.
Exponentieller Zerfall
Man nimmt an, dass ein Vorgang die Menge einer Substanz mit einer festen Zerfallskonstante verringert. Dies bedeutet, dass während einer kurzen Zeitspanne sich die Menge um ändert, also der -te Teil der aktuellen Substanzmenge zerfällt. Daraus ergibt sich eine einfache Differentialgleichung, die diesen Vorgang beschreibt:
Diese Gleichung hat als Lösung eine Exponentialfunktion
wobei die Anfangsmenge der Substanz ist. Die Halbwertszeit ist nun die Zeit , nach der nur noch die Hälfte der Substanz vorhanden ist, es gilt also . Daraus ergibt sich durch Einsetzen
und allgemeiner für die Zeit , nach der nur noch der -te Teil der Substanz vorhanden ist, für die also gilt,
Allgemeiner Zerfall
Für allgemeinere Zerfälle ist die Definition für die Halbwertszeit weiterhin
allerdings folgt dann die Größe keiner einfachen Exponentialfunktion mehr.
Ein Beispiel hierfür sind chemische Reaktionen zweiter Ordnung, wie etwa Dimerisierungen der Form
bei denen sich immer zwei Moleküle N zu einem Molekül P verbinden. Die Ratengleichung hierfür ist eine gewöhnliche Differentialgleichung, die den Zerfall beschreibt:[13]
Hierbei ist die Reaktionsgeschwindigkeitskonstante und die Reaktionsgeschwindigkeit. Die Lösung dieser Gleichung ist dann
und die Halbwertszeit ergibt sich zu
Im Gegensatz zum exponentiellen Fall hängt hier nicht nur von der Reaktionsgeschwindigkeitskonstante ab, sondern explizit auch von der Ausgangsmenge ; „Halbwertszeit“ bezeichnet hier also immer die Zeit, nach der die Ausgangsmenge sich halbiert hat. Die Zeit , nach der der -te Teil der Substanz zerfallen ist, ergibt sich zu
Weblinks
- Rechenhilfe zur Aktivität nach wählbarer Abklingzeit mit fast 4500 frei wählbaren Nukliden.
Einzelnachweise
- Duden.
- Otto-Albrecht Neumüller (Hrsg.): Römpps Chemie-Lexikon. Band 3: H–L. 8. neubearbeitete und erweiterte Auflage. Franckh’sche Verlagshandlung, Stuttgart 1983, ISBN 3-440-04513-7, S. 1612–1613.
- A. Wallner u. a.: Physical Review Letters. Bd. 114 (2015) 041101.
- E. B. Paul: Nuclear and Particle Physics. North-Holland 1969, S. 47–49.
- J. Magill, G. Pfennig, R. Dreher, Z. Sóti: Karlsruher Nuklidkarte. 8. Auflage 2012. Nucleonica GmbH 2012, ISBN 92-79-02431-0 (Wandkarte) bzw. ISBN 978-3-00-038392-2 (Faltkarte).
- KAERI-Nuklidkarte.
- E. Rutherford: A Radioactive Substance emitted from Thorium Compounds. In: Philosophical Magazine. Ser. 5, 49, Seite 1–14 (1900).
- Jörn Bleck-Neuhaus: Elementare Teilchen. Von den Atomen über das Standard-Modell bis zum Higgs-Boson. 2., überarbeitete Auflage. Springer, 2013, ISBN 978-3-642-32578-6, ISSN 0937-7433, S. 157–159, doi:10.1007/978-3-642-32579-3.
- S. Ebel, H. J. Roth (Hrsg.): Lexikon der Pharmazie. Georg Thieme Verlag, 1987, S. 307, ISBN 3-13-672201-9.
- Malcolm Rowland und Thomas N. Tozer: Clinical Pharmacokinetics. Philadelphia 1980, S. 91, ISBN 0-8121-0681-4.
- P. F. Cole: A new look at reference scattering. In: Journal of Documentation. 18 (1962), S. 58–64.
- W. Umstätter, M. Rehm, Z. Dorogi: Die Halbwertszeit in der naturwissenschaftlichen Literatur. (Memento vom 27. September 2011 im Internet Archive). In: Nachr. f. Dok. 33 (1982), S. 50–52, abgerufen am 5. Mai 2015.
- Peter Atkins, Julio de Paula: Atkins’ Physical Chemistry. Oxford University Press, 2010, ISBN 978-0-19-954337-3, S. 793–795 (google.de).