Gleitsystem

Die Gleitebenen bilden in einem Kristall die Ebenen zwischen Atomlagen mit dichtester Packung und großem Schichtabstand. In ihnen findet bei Verformung die Versetzungsbewegung statt, da die relativ kleinste kritische Schubspannung benötigt wird.

Gleitebenen werden mit den in der Kristallographie üblichen millerschen Indizes gekennzeichnet. Typische Beispiele sind

• die {111}-Ebene im kubisch-flächenzentrierten Gitter (kfz, engl. fcc)
• die {110}- und {112}-Ebenen im kubisch-raumzentrierten Gitter (krz, engl. bcc)
• die {0001}-Gleitebene im hexagonalen Kristallsystem (hex, engl. hcp) (meistens).

• 
  {111}-Gleitebene in einem kubisch-flächenzentrierten Gitter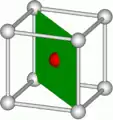
• 
  {110}-Gleitebene in einem kubisch-raumzentrierten Gitter

In Molekülkristallen mit komplizierter Struktur können sich die Gleitsysteme auch nach anderen Auswahlregeln richten. So wurde bei zwei isomorphen triklinen TCNQ-Komplexsalzen gefunden, dass die Gleitebene (010) parallel zu einer Art Gasse in der Struktur orientiert ist, welche nicht von Teilen der Moleküle gekreuzt wird, so dass Gleitung in den Gleitrichtungen [${\displaystyle 101}$], [${\displaystyle 10{\bar {1}}}$] und deren Gegenrichtungen erfolgen kann, ohne dass die Moleküle selbst beschädigt werden.[1]

Gleitrichtung und Burgersvektor im kfz-Gitter

Gleitrichtung und Burgersvektor im krz-Gitter

Die Gleitrichtung ist die Richtung der dich(tes)ten Atompackung und somit die Richtung, in die das Gleiten der Atomschichten mit relativ kleinstem Energieaufwand möglich ist.

Typische Beispiele sind[2]

• im kubisch-flächenzentrierten Gitter die <110>-Richtung um den Betrag: ${\displaystyle |b|={\frac {a}{2}}|\langle 110\rangle |={a{\frac {\sqrt {2}}{2}}}}$
• im kubisch-raumzentrierten Gitter die <111>-Richtung um den Betrag: ${\displaystyle |b|={\frac {a}{2}}|\langle 111\rangle |=a{\frac {\sqrt {3}}{2}}}$
• im hexagonalen Kristallsystem meistens die <1120>-Richtung um den Betrag ${\displaystyle |b|=a}$

Aus den möglichen Gleitebenen und Gleitrichtungen ergeben sich verschiedene mögliche Gleitsysteme.

Die unterschiedlichen Gleitsysteme erklären auch die unterschiedlich gute Verformbarkeit der Kristallstrukturen: In kfz- und krz-Strukturen sind Systeme des gleichen Typs räumlich gleichmäßig verteilt. Dagegen ermöglichen in hex-Strukturen die leicht aktivierbaren {0001}<1120>-Systeme eine Bewegung nur in einer Ebene; daher ist hier für beliebige Verformungen immer der Beitrag der anderen Gleitsysteme (oder die mechanische Zwillingsbildung) notwendig, was aber in der Regel eine deutlich höhere Spannung benötigt.

Kritische Schubspannung ${\displaystyle \tau _{0}}$ im Idealkristall an Beispielen der theoretischen Schubspannung ${\displaystyle \tau _{th}}$ als 0,1 des Schubmodul[6]

Schubspannung	Cu (kfz)	Fe (krz)	Cd (hex)
${\displaystyle \tau _{th}}$	4200	8000	200
${\displaystyle \tau _{0}}$	0,6	14	0,5

• G. Gottstein: Physikalische Grundlagen der Metallkunde. 3. Auflage. Springer, Berlin 2007, ISBN 978-3-540-71104-9.
• Gustav E. R. Schulze: Metallphysik. 2. Auflage. Springer, Wien 1974, ISBN 3-211-81113-3.

1. Heinz H. W. Preuß: Trikline TCNQ-Komplexsalze als Modellkörper zur Untersuchung der Kristallplastizität bei niederer Symmetrie, Dissertation B (Habilitationsschrift) Leipzig, 1977. In: Freiberger Forschungsheft. B 204. VEB Deutscher Verlag für Grundstoffindustrie, Leipzig 1978.
2. Van Vliet, Krystyn J. (2006); "3.032 Mechanical Behavior of Materials"
3. damask.mpie.de/Documentation/FCC, Übersicht aller Systeme und Kugelmodell.
4. damask.mpie.de/Documentation/BCC, Übersicht aller Systeme und Kugelmodell.
5. damask.mpie.de/Documentation/hex, Übersicht aller Systeme und Kugelmodell.
6. Wolfgang Weißbach: Werkstoffkunde : Strukturen, Eigenschaften, Prüfung. 16. Auflage. Vieweg, Wiesbaden 2007, ISBN 978-3-8348-0295-8.