Gauß-Filter

Gauß-Filter sind Frequenzfilter, welche bei der Sprungantwort keine Überschwingung und gleichzeitig maximale Flankensteilheit im Übergangsbereich aufweisen. Als Besonderheit besitzt bei diesem Filter sowohl die Übertragungsfunktion als auch die Impulsantwort den Verlauf einer gaußschen Glockenkurve, wie in den Abbildungen dargestellt, wovon sich auch der Name dieses Filtertyps ableitet.

Betragsfrequenzgang

\left\vert H(j\omega )\right\vert

eines Gauß-Filters mit normierter Frequenz und einer Bandbreite

B

von 1.

Impulsantwort

h(t)

eines Gauß-Filters

Anwendungsbereiche dieses Filters liegen bei digitalen Modulationsverfahren und im Bereich der Bildverarbeitung.

Ein Gauß-Filter faltet das Eingangssignal mit einer Gauß-Verteilung, um die Glättung zu erzielen.

Binomialfilter approximieren Gauß-Filter effizient und nutzen dabei, dass die (diskrete) Binomialverteilung der (kontinuierlichen) Gauß-Verteilung ähneln kann.

Eigenschaften

Ein Filter wird als Gauß-Filter bezeichnet, wenn die geschätzten Dichten über dem unbekannten Zustand durch Gauß-Dichten dargestellt werden. Gauß-Filter sind insbesondere für höherdimensionale Systeme attraktiv, da sie normalerweise einfacher zu implementieren sind als Filter, die mit komplexeren Arten von Dichten arbeiten. Die Rechenanforderungen sind typischerweise niedriger und die Schätzung kann kompakt durch den mittleren Vektor und die Kovarianzmatrix dargestellt werden.

Andererseits ist die einfache Dichtedarstellung in einigen Fällen nicht ausreichend, um die Zustandsschätzung darzustellen. Darüber hinaus gibt es verschiedene Arten von Gauß-Filtern, die weitere Annahmen treffen, beispielsweise eine zweite Gaußsche Annahme zwischen Zustand und Messung. Diese Filter erreichen natürlich nicht die Leistung von Filtern, die nur die Zustandsschätzungen als Gauß-Filter festlegen. Ohne zusätzliche Annahmen sind Gauß-Filter jedoch weitaus schwieriger zu entwerfen.[1]

Definition

Der eindimensionale Gauß-Filter hat eine Impulsantwort, die durch

g(x)={\sqrt {\frac {a}{\pi }}}\cdot {\text{e}}^{-a\cdot x^{2}}

gegeben ist und der Frequenzgang ist durch die Fourier-Transformation gegeben

{\hat {g}}(f)={\text{e}}^{-{\frac {\pi ^{2}f^{2}}{a}}}

wobei $f$ die gewöhnliche Frequenz ist. Diese Gleichungen können auch mit der Standardabweichung als Parameter ausgedrückt werden:

g(x)={\frac {1}{{\sqrt {2\pi }}\cdot \sigma }}\cdot {\text{e}}^{-{\frac {x^{2}}{2\sigma ^{2}}}}

und der Frequenzgang ist gegeben durch

{\hat {g}}(f)={\text{e}}^{-{\frac {f^{2}}{2\sigma _{f}^{2}}}}

Indem $a$ als Funktion von $\sigma$ mit den beiden Gleichungen für $g(x)$ und als Funktion von $\sigma _{f}$ mit den beiden Gleichungen für ${\hat {g}}(f)$ geschrieben wird, kann gezeigt werden, dass das Produkt der Standardabweichung und der Standardabweichung im Frequenzband gegeben ist durch

\sigma \cdot \sigma _{f}={\frac {1}{2\pi }}

wobei die Standardabweichungen in ihren physikalischen Einheiten ausgedrückt werden, z. im Fall von Zeit und Frequenz in Sekunden bzw. Hertz.

In zwei Dimensionen ist es das Produkt von zwei solchen Gauß-Filtern, einer pro Richtung:

g(x,y)={\frac {1}{2\pi \sigma ^{2}}}\cdot {\text{e}}^{-{\frac {x^{2}+y^{2}}{2\sigma ^{2}}}}

Dabei ist $x$ der Abstand vom Ursprung auf der horizontalen Achse, $y$ der Abstand vom Ursprung auf der vertikalen Achse und $\sigma$ die Standardabweichung der Normalverteilung.[2]

Übertragungsfunktion

Der Betrag der Übertragungsfunktion $H(j\omega )$ ist bei Gauß-Filtern gegeben durch

|H(j\omega )|={\text{e}}^{-\left({\frac {\omega }{2\alpha }}\right)^{2}}

mit der Konstanten $\alpha$

\alpha ={\frac {\pi }{\sqrt {\ln({\sqrt {2}})}}}

.

Die Impulsantwort eines Gauß-Filters lautet

h(t)={\frac {\alpha }{\sqrt {\pi }}}{\text{e}}^{{-(\alpha t)}^{2}}

.

Daraus ist ersichtlich, dass das Gauß-Filter eine Idealisierung darstellt, denn es ist nicht-kausal: Die Hälfte der Impulsantwort (Verlauf bei t < 0) ist am Ausgang des Filters bereits erschienen, wenn am Eingang des Filters das auslösende Signal, der Impuls, bei t = 0 auftritt.

Anwendungen

Digitale Signalverarbeitung

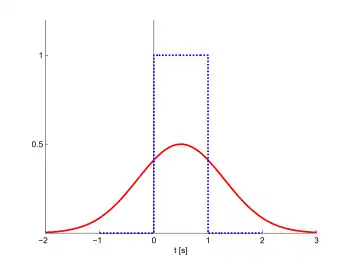
Ein Rechteckimpuls, blau punktiert dargestellt, wird durch die Impulsformung eines Gauß-Filters in den rot dargestellten Signalverlauf übergeführt.

Gauß-Filter besitzen eine konstante Gruppenlaufzeit im Sperr- und Durchlassbereich und kein Überschwingen in der Sprungantwort[3]. Einsatzbereich dieses Filters liegt primär zur Impulsformung mit Anwendungsbereichen in der digitalen Signalverarbeitung.

Die Impulsformung findet bei digitalen Modulationsverfahren wie dem Gaussian Minimum Shift Keying (GMSK), da damit die einzelnen, meist rechteckförmigen Sendesymbole in Impulse der gaußschen Glockenkurve mit geringerem Bandbreitenbedarf als die ursprünglichen rechteckförmigen Sendesymbole umgewandelt werden können. Damit ist eine höhere spektrale Effizienz des Modulationsverfahrens verbunden.

In Mobilfunksystemen wie GSM werden Gauß-Filter im Rahmen der GMSK-Modulation auf der Funkschnittstelle zur Übertragung der digitalen Sprach- und Steuerinformationen eingesetzt.

Weitere Anwendungen liegen bei Modulationstechniken wie dem Chirp Spread Spectrum, bei dem die unstetige Frequenzänderung bei zeitlich aufeinanderfolgenden Chirps durch Gauß-Filter geglättet wird.

Bildverarbeitung

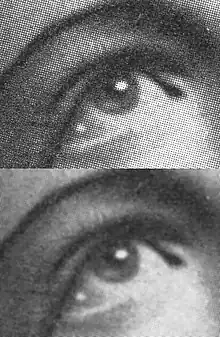
Mit einem Gauß-Filter geglättetes Halbtonbild

In der Bildverarbeitung werden Gauß-Filter zur Glättung oder Weichzeichnen des Bildinhaltes verwendet. Es kann damit das Bildrauschen vermindert werden: Kleinere Strukturen gehen verloren, gröbere Strukturen bleiben dagegen erhalten[4]. Spektral kommt die Glättung einem Tiefpassfilter gleich.

Da ein Bild zwei Dimensionen aufweist, muss für die Bildverarbeitung die Impulsantwort auf zwei Dimensionen erweitert werden. Die Impulsantwort besitzt die beiden Argumente $x$ und $y$ entsprechend den Raumrichtungen:

h(x,y)={\frac {\alpha ^{2}}{\pi }}{\text{e}}^{-\alpha ^{2}(x^{2}+y^{2})}

.

Für praktische Realisierungen im Rahmen der digitalen Bildverarbeitung wird die diskrete Impulsantwort meist in Form einer zweidimensionalen Matrix verwendet.

Alternativ wird in der Literatur bei der Beschreibung von Gauß-Filtern statt der Konstanten $\alpha$ dazu gleichwertig die Varianz $\sigma ^{2}$ in dem Ausdruck der Impulsantwort verwendet – was die mathematische Nähe der Impulsantwort eines Gauß-Filters zur Funktion der Normalverteilung ausdrückt. Bei einer Dimension ist die Impulsantwort:

h(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}{\text{e}}^{-{\frac {x^{2}}{2\sigma ^{2}}}}

Die Impulsantwort bei zwei Dimensionen ergibt sich aus dem Produkt der beiden Richtungen in x und y:

h(x,y)={\frac {1}{{2\pi }\sigma ^{2}}}{\text{e}}^{-{\frac {x^{2}+y^{2}}{2\sigma ^{2}}}}

Durch Ausnutzung der Separierbarkeit kann die Rechenzeit deutlich reduziert werden.

Literatur

Karl Dirk Kammeyer, Volker Kühn: MATLAB in der Nachrichtentechnik. 1. Auflage. J. Schlembach Fachverlag, 2001, ISBN 3-935340-05-2.

Einzelnachweise

Uwe D. Hanebeck, Karlsruhe Institute of Technology: Progressive Gaussian Filteringwith a Twist
Richard A. Haddad and Ali N. Akansu, New Jersey Institute of Technology: A Class of Fast Gaussian Binomial Filters for Speech and Image Processing
F. Dellsperger: Passive Filter. Berner Fachhochschule, Hochschule für Technik und Informatik HTI, Fachbereich Elektro- und Kommunikationstechnik, 2012, S. 25, abgerufen am 17. Juli 2017.
Beispiel: Entfernen von Gravurlinien (Memento vom 10. März 2010 im Internet Archive) für den Vergleich größerer Strukturen in einem Holzstich (1876, Henry Holiday) und in einer Radierung (1566–1568, Markus Gheeraerts der Ältere).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Uwe D. Hanebeck, Karlsruhe Institute of Technology: Progressive Gaussian Filteringwith a Twist

[2] Richard A. Haddad and Ali N. Akansu, New Jersey Institute of Technology: A Class of Fast Gaussian Binomial Filters for Speech and Image Processing

[dell1-3] F. Dellsperger: Passive Filter. Berner Fachhochschule, Hochschule für Technik und Informatik HTI, Fachbereich Elektro- und Kommunikationstechnik, 2012, S. 25, abgerufen am 17. Juli 2017.

[4] Beispiel: Entfernen von Gravurlinien (Memento vom 10. März 2010 im Internet Archive) für den Vergleich größerer Strukturen in einem Holzstich (1876, Henry Holiday) und in einer Radierung (1566–1568, Markus Gheeraerts der Ältere).