Eulersche Scheibe

Dreht man die Eulersche Scheibe, so beginnt sie sich entlang der Rotationsachse zu drehen und auch die Rotationsachse selbst bewegt sich. Mit der Zeit werden die Bewegungen immer schneller. Da die Kanten immer häufiger auf die Oberfläche prallen, erhöht sich die Lautstärke. Auch visuell verschmelzen die Bewegungen.

Nach Angaben des Erfinders sei die Idee des Spielzeugs Ende der 1990er-Jahre entstanden, als er Ingenieur eines größeren Unternehmens in Südkalifornien war. Durch eine Fehllieferung wurden damals zwölf rasiermesserscharfe Scheiben an ihn geliefert. Aus Langeweile fing er an, eine Scheibe auf seinem glatten Schreibtisch zu drehen, wodurch nach einer knappen halben Minute ein Kollege in sein Büro kam und sich wegen des Lärms erkundigte.[1]

Illustration

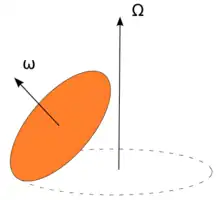
Im Wesentlichen ist die Erklärung, weshalb die Eulersche Scheibe sich so dreht, nicht anders als etwa bei Münzen. Wegen ihrer glatten Oberfläche und abgerundeten Kante dreht sie sich aber besonders lange – je nach Durchmesser und Masse mehrere Minuten. Zur Erklärung muss man Reibung und Luftwiderstand beachten. Wenn man die für die Erdatmosphäre typische Viskosität und die Erdbeschleunigung ${\displaystyle g}$ hat, dann hängt im Wesentlichen die Drehung von der Masse ${\displaystyle M}$, dem Durchmesser ${\displaystyle d}$ und dem anfänglichen Winkel ${\displaystyle \alpha _{0}}$ ab. Während des Drehens strebt der Winkel ${\displaystyle \alpha \leq \alpha _{0}}$ gegen ${\displaystyle 0}$. Dann kann man zwei Größen beobachten:[2]

• Die Winkelgeschwindigkeit ${\displaystyle \omega }$, die besagt, mit welcher Geschwindigkeit sich die Scheibe um die eigene Achse dreht. Die Winkelgeschwindigkeit beträgt

${\displaystyle \vert \omega \vert =-2\cdot {\sqrt {\frac {g\sin(\alpha )}{d}}}.}$

• Die Präzession ${\displaystyle \Omega }$, welche die Richtungsänderung der Rotationsachse beschreibt. Dabei gilt

${\displaystyle \vert \Omega \vert =2\cdot {\sqrt {\frac {g}{d\sin(\alpha )}}}.}$

Die Frequenz, mit der die Scheibe die Oberfläche berührt, beträgt dann

${\displaystyle {\frac {\vert \Omega \vert }{2\pi }}={\frac {1}{\pi }}\cdot {\sqrt {\frac {g}{d\sin(\alpha )}}}.}$

Für kleiner werdende ${\displaystyle \alpha }$ wächst also die Frequenz stark an, was die Lautstärke und optische Illusion (Flimmerverschmelzungsfrequenz) erklärt.

Anfang der 2000er-Jahre wurde die Eulersche Scheibe Gegenstand mehrerer wissenschaftlicher Veröffentlichungen, bei denen es um die Frage ging, ob vornehmlich der Luftwiderstand oder die Reibung die besonders „wackelig“ aussehenden Bewegungen verursachten. Keith Moffatt vermutete, es liege an dünnen Luftschichten. Er berechnete für eine 400 g schwere Scheibe mit einem Radius von 3,75 cm eine Drehzeit von 80 bis 120 Sekunden, was mit empirischen Beobachtungen übereinstimmte.[3] Allerdings führte man im Anschluss experimentelle Versuche im Vakuum oder bei sehr niedrigem Luftdruck durch, die diese Hypothese eher widerlegten.[4][5][6] Es besteht daher Übereinstimmung, dass vornehmlich die Reibung den Effekt verursacht.

Commons: Eulersche Scheibe – Sammlung von Bildern und Videos

• Erklärvideo von Michael Stevens
• Drehung der Eulerschen Scheibe in normaler Geschwindigkeit
• Drehung der Eulerschen Scheibe, 10-mal verlangsamt

1. Joseph Bendik: The History of Euler’s Disk. In: eulerdisk.com. 2020, abgerufen am 14. März 2024 (englisch).
2. Die Berechnungen für die Formeln kann man finden unter: Alexander J. McDonald, Kirk T. McDonald: The Rolling Motion of a Disk on a Horizontal Plane, 5. April 2002, arxiv:physics/0008227.
3. Keith Moffatt: Euler’s Disk and its Finite-time Singularity: Nature, Bd. 404, 20. April 2000, S. 833 f.
4. Ger van den Engh, Peter Nelson, Jared Roach: Analytical dynamics: Numismatic gyrations, Nature, Bd. 408, S. 540.
5. D. Petrie, J. L. Hunt, C. G. Gray: Does the Euler Disk slip during its motion? American Journal of Physics, Bd. 70, Nr. 10, 2002, S. 983.
6. H. Caps, S. Dorbolo, S. Ponte, H. Croisier, and N. Vandewalle: Rolling and slipping motion of Euler’s disk, Phys. Rev. E 69, 056610 (2004).