Dreieckszahl

Eine Dreieckszahl ist eine Zahl, die der Summe aller natürlichen Zahlen von 1 bis zu einer Obergrenze $n$ entspricht. Beispielsweise ist die 10 eine Dreieckszahl, da $1+2+3+4=10$ ist. Die ersten Dreieckszahlen sind:

0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, … (Folge A000217 in OEIS)

Ein Dreieck aus zehn Steinen

Bei einigen Autoren ist die Null keine Dreieckszahl, sodass die Zahlenfolge erst mit der Eins beginnt.

Die Bezeichnung Dreieckszahl leitet sich von der geometrischen Figur des Dreiecks her. Die Anzahl der Steine, die man zum Legen eines gleichseitigen Dreiecks benötigt, entspricht immer einer Dreieckszahl. Aus zehn Steinen lässt sich beispielsweise ein Dreieck legen, bei dem jede Seite von vier Steinen gebildet wird.

Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Dreieckszahlen zu den figurierten Zahlen, zu denen auch die Quadratzahlen und Kubikzahlen gehören. Schon Pythagoras hat sich mit Dreieckszahlen beschäftigt.[1]

Berechnung

Eine Möglichkeit, die (rot geschriebenen) Dreieckszahlen zu bestimmen

Die $n$ -te Dreieckszahl ist die Summe der natürlichen Zahlen von 1 bis $n$ .

{\begin{aligned}\Delta _{1}&=1&=&\ 1\\\Delta _{2}&=1+2&=&\ 3\\\Delta _{3}&=1+2+3&=&\ 6\\\Delta _{4}&=1+2+3+4&=&\ 10\\&\qquad \vdots &\end{aligned}}

Anstatt die einzelnen Zahlen zu addieren, können Dreieckszahlen auch durch die gaußsche Summenformel berechnet werden:

\Delta _{n}={\frac {n\cdot (n+1)}{2}}

Die rechte Seite ist identisch mit dem Binomialkoeffizienten $n+1$ über 2:

\Delta _{n}={n+1 \choose 2}

Diese Formel lässt sich durch Auslegen der Dreieckszahl veranschaulichen. Die Dreieckszahl lässt sich als Dreieck oder Treppe auslegen. Das Doppelte einer Dreieckszahl entspricht zwei gleichen Treppen, die sich zu einem Rechteck zusammenfügen lassen.

Dieses Rechteck ist $n$ Kugeln hoch und $n+1$ Kugeln breit und enthält somit $n\cdot (n+1)$ Kugeln. Eine Dreieckszahl entspricht der Hälfte der Kugeln, woraus sich die oben genannte Formel für Dreieckszahlen ergibt.

Eigenschaften

Bei allen Dreieckszahlen > 3 handelt es sich um zusammengesetzte Zahlen.
Die Summe der ersten n Kubikzahlen ist gleich dem Quadrat der n-ten Dreieckszahl [Bsp.: 1 + 8 + 27 + 64 = 100 = 10²]
Die Differenz der Quadrate zweier aufeinander folgender Dreieckszahlen ergibt eine Kubikzahl.
Dies lässt sich aus der darüber stehenden Eigenschaft ableiten. Da das Quadrat der n-ten Dreieckszahl aus der Summe der ersten n Kubikzahlen gebildet wird und das Quadrat der (n+1)-ten Dreieckszahl aus der Summe der ersten n+1 Kubikzahlen gebildet wird, muss als Differenz die (n+1)-te Kubikzahl herauskommen.
Jede gerade vollkommene Zahl ist auch eine Dreieckszahl:
Nach Leonhard Euler lässt sich eine gerade vollkommene Zahl durch die Formel $(2^{n}-1)\cdot 2^{n-1}$ darstellen, wobei $2^{n}-1\$ eine Primzahl (Mersenne-Primzahl) sein muss. Wenn man die Formel $(2^{n}-1)\cdot 2^{n-1}$ mit 2 erweitert und $2^{n}\$ durch $m\$ substituiert, kommt man auf die Formel, die eine Dreieckszahl darstellt:

(2^{n}-1)\cdot 2^{n-1}={\frac {(2^{n}-1)\cdot 2^{n-1}\cdot 2}{2}}={\frac {(2^{n}-1)\cdot 2^{n}}{2}}={\frac {(m-1)\cdot m}{2}}

Die Summe zweier Dreieckszahlen ist nicht kongruent 5 (mod 9).
$\Delta _{n}\equiv \{1,n/2+2\}\mod {n+2}$ , wenn $n=\{ungerade,gerade\}$ .
Es gilt: $\Delta _{n+1}=(2n+1)+\Delta _{n-1}.$
Das Achtfache einer Dreieckszahl plus 1 ergibt eine ungerade Quadratzahl: $8\cdot \Delta _{n}+1=(2n+1)^{2}$


n=3 (7 Reihen)	n=4 (9 Reihen)

Auch die nachfolgenden Beziehungen zwischen Dreieckszahlen lassen sich für n = 5 grafisch veranschaulichen.[2]

3\Delta _{n}+\Delta _{n-1}=\Delta _{2n}

(Abb. 1)

3\Delta _{n}+\Delta _{n+1}=\Delta _{2n+1}

(Abb. 2)

\Delta _{n-1}+6\Delta _{n}+\Delta _{n+1}=(2n+1)^{2}

(Abb. 3)

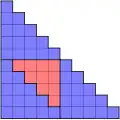Abb. 1
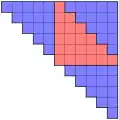Abb. 2
Abb. 3

Die n-te Dreieckszahl ist gleich der Differenz der n-ten zentrierten Neuneckszahl und der n-ten zentrierten Achteckszahl:

\Delta _{n}=(1+3n)\cdot (2+3n)/2-(1+2n)^{2}

.

Diese Identität (mit der jeweils n-ten) ist die Minimallösung von jeweils abzählbar unendlich vielen Lösungen (siehe hier).

Addiert man zu den Dreieckszahlen jeweils Eins, so erhält man die Folge der zentralpolygonalen Zahlen (auch Zahlenfolge des faulen Kellners) genannt:

1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56, 67, 79, 92, 106, 121, 137, 154, 172, 191, 211, …(Folge A000124 in OEIS)

Summe dreier Dreieckszahlen

Pierre de Fermat stellte die Vermutung auf, dass sich jede natürliche Zahl als Summe von höchstens drei Dreieckszahlen darstellen lässt. Diese Vermutung wurde von Carl Friedrich Gauß bewiesen, der am 10. Juli 1796 in sein Tagebuch schrieb:[3]

EYPHKA num = Δ + Δ + Δ.

Die allgemeinere Aussage ist als fermatscher Polygonalzahlensatz bekannt.

Beziehungen zu Quadratzahlen

Nachfolger der Summe zweier vierfacher Dreieckszahlen

{\begin{aligned}4\cdot \Delta _{i}+4\cdot \Delta _{j}+1&=(i-j)^{2}+(1+i+j)^{2}\end{aligned}}

Der Nachfolger der Summe zweier vierfacher Dreieckszahlen ist die Summe zweier Quadratzahlen verschiedener Parität.

Summe zweier aufeinanderfolgender Dreieckszahlen

10 + 15 = 25

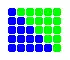
Die Summe zweier aufeinanderfolgender Dreieckszahlen ergibt eine Quadratzahl. Das nebenstehende Bild zeigt beispielhaft, wie sich die Dreieckszahlen $\Delta _{4}=10$ und $\Delta _{5}=15$ zur Quadratzahl 25 addieren.

Dieses Phänomen lässt sich auch durch eine Formel beschreiben.

{\begin{aligned}\Delta _{n-1}+\Delta _{n}&={\frac {n(n-1)}{2}}+{\frac {(n+1)n}{2}}\\&=n^{2}\end{aligned}}

Für eine andere Erklärung dieses Phänomens zerlegt man die Dreieckszahl ${\frac {n\cdot (n+1)}{2}}$ in die Summe von $n$ und der vorhergehenden Dreieckszahl ${\frac {(n-1)\cdot n}{2}}$ : . Dementsprechend gilt $2\cdot {\frac {(n-1)\cdot n}{2}}+n=(n-1)\cdot n+n=n^{2}-n+n=n^{2}$

Dass sich zwei aufeinanderfolgende Dreieckszahlen zu einer Quadratzahl addieren, wurde schon im 2. Jahrhundert vom griechischen Mathematiker Theon von Smyrna in seinem Werk „Das an mathematischem Wissen für die Lektüre Platons Nützliche“ niedergeschrieben.[4]

Alternierende Summe von Quadratzahlen

Nimmt man die Quadratzahl $n^{2}$ und subtrahiert und addiert abwechselnd die kleineren Quadratzahlen, dann erhält man als Ergebnis die $n$ -te Dreieckszahl. Beispielsweise berechnen sich die vierte und fünfte Dreieckszahl wie folgt:

16-9+4-1=10=\Delta _{4}

25-16+9-4+1=15=\Delta _{5}

Indem man sich zunutze macht, dass jede Quadratzahl die Summe zweier aufeinanderfolgender Dreieckszahlen ist, kann man diesen Zusammenhang anhand seiner geometrischen Veranschaulichung erklären.

Man sieht, dass (mit Ausnahme des größten) jedes Dreieck in der Summe genau zweimal vorkommt: je einmal mit Plus und mit Minus. Dadurch heben sich die kleinen Dreiecke in der Summe gegenseitig auf, und übrig bleibt allein das große Dreieck.

Mit Hilfe des mathematischen Wortschatzes lässt sich obiger Sachverhalt sehr kurz wiedergeben: Die $n$ -te Dreieckszahl ist die alternierende Summe der Quadratzahlen von $n^{2}$ bis 1. Die entsprechende mathematische Formel ist

\Delta _{n}=\sum _{i=1}^{n}(-1)^{n+i}\cdot i^{2}

Quadrat-Dreieckszahlen

Quadrat-Dreieckszahlen sind Dreieckszahlen, die gleichzeitig Quadratzahlen sind. Die ersten Quadrat-Dreieckszahlen sind

0, 1, 36, 1225, 41616, 1413721, 48024900, 1631432881, … Folge A001110 in OEIS

Dies sind die Dreieckszahlen mit den Indizes

0, 1, 8, 49, 288, 1681, 9800, 57121, … Folge A001108 in OEIS

Damit eine Dreieckszahl eine Quadratzahl sein kann, muss für diese Zahl

{\frac {n\cdot (n+1)}{2}}

Folgendes gelten: Von den beiden Zahlen $n+1\$ und $n\$ muss eine der beiden eine ungerade Quadratzahl sein, während die andere das Doppelte einer Quadratzahl sein muss. Denn die beiden aufeinanderfolgenden Zahlen sind immer teilerfremd; insbesondere ist immer eine der beiden ungerade, und die andere ist gerade. Die gerade Zahl ist deshalb das Doppelte einer Quadratzahl, und die ungerade Zahl ist selbst eine (ungerade) Quadratzahl.

Die Quadrat-Dreieckszahlen lassen sich wie folgt errechnen:

1^{2}\cdot 1^{2}

2^{2}\cdot 3^{2}

5^{2}\cdot 7^{2}

12^{2}\cdot 17^{2}

29^{2}\cdot 41^{2}

70^{2}\cdot 99^{2}

169^{2}\cdot 239^{2}

Hierbei ist die erste Basis jeder Zeile die Summe der beiden Basen der vorausgehenden Zeile, und die zweite Zahl ist um die erste Zahl der Vorzeile höher:

m^{2}\cdot n^{2}

(m+n)^{2}\cdot (2m+n)^{2}

Da sich der Quotient ${\frac {n^{2}}{m^{2}}}$ asymptotisch der $2$ nähert, nähert sich ${\frac {n}{m}}$ asymptotisch dem Wert ${\sqrt {2}}$ . Daraus folgt, dass der Faktor, um von einer Quadrat-Dreieckszahl zur nächsten zu gelangen, asymptotisch den Wert $(1+{\sqrt {2}})^{4}=17+12\cdot {\sqrt {2}}$ anstrebt.

Die Quadrat-Dreieckszahlen sind immer abwechselnd gerade und ungerade, mit 36er-Rest im Wechsel 0 und 1. Die geraden lassen sich aus einer kleineren Quadrat-Dreieckszahl $n$ nach der Formel $4\cdot n\cdot (8\cdot n+1)$ berechnen.

Dreieckszahlen und zentrierte Polygonalzahlen

Zentrierte Polygonalzahlen stehen im Zusammenhang mit regelmäßigen Polygonen, die nach folgendem Muster gelegt werden: Ein einzelner Stein liegt im Mittelpunkt des Polygons. Um diesen Stein werden weitere Polygone gelegt, wobei sich deren Seitenlängen von innen nach außen jeweils um eins erhöhen.

Diese Muster können auch nach einer anderen Regel gelegt werden. Wieder wird mit dem einzelnen Stein in der Mitte begonnen. Doch im zweiten Schritt werden für die $n$ -te zentrierte $k$ -Eckszahl $k$ Dreiecke nach dem Muster der $(n-1)$ -ten Dreieckszahl um das Zentrum herumgelegt. Das folgende Bild zeigt dies für die erste bis vierte zentrierte Quadratzahl.

Daraus folgt für die $n$ -te zentrierte $k$ -Eckszahl folgende Formel:

1+k\cdot \Delta _{n-1}=1+{\frac {kn(n-1)}{2}}

Die Summe dreier aufeinanderfolgender Dreieckszahlen ist eine zentrierte Dreieckszahl. Da bei Dreieckszahlen der Modul 3 den Zyklus (1,0,0) aufweist, ist jede zentrierte Dreieckszahl äquivalent 1 (mod 3).

Zahlenpalindrome unter den Dreieckszahlen

Unter den Dreieckszahlen gibt es mehrere Zahlenpalindrome. Beispiele sind

1, 3, 6, 55, 66, 171, 595, 666, 3003, 5995, 8778, … (Folge A003098 in OEIS)

Unter diesen sind die 11te, die 1.111te, die 111.111te und die 11.111.111te Dreieckszahl. Für die 1.111te und die 111.111te Dreieckszahl hat dies Charles Trigg herausgefunden.

Reihe der Kehrwerte

Geometrische Interpretation der Kehrwertreihe[5]

Die Summe der Kehrwerte aller Dreieckszahlen ist

\sum _{n=1}^{\infty }{\frac {1}{\Delta _{n}}}={\frac {2}{1\cdot 2}}+{\frac {2}{2\cdot 3}}+{\frac {2}{3\cdot 4}}+\dots =2

Lösung nach Gottfried Wilhelm Leibniz, mit ${\frac {1}{\Delta _{n}}}={\frac {2}{n(n+1)}}={\frac {2(n+1)-2n}{n(n+1)}}={\frac {2}{n}}-{\frac {2}{n+1}}$ ,

{\begin{aligned}1/\Delta _{1}&={\tfrac {1}{1}}&={\tfrac {2}{1}}\color {Red}-{\tfrac {2}{2}}\\1/\Delta _{2}&={\tfrac {1}{3}}&=\color {Red}{\tfrac {2}{2}}-{\tfrac {2}{3}}\\1/\Delta _{3}&={\tfrac {1}{6}}&=\color {Red}{\tfrac {2}{3}}-\color {Red}{\tfrac {2}{4}}\\1/\Delta _{4}&={\tfrac {1}{10}}&=\color {Red}{\tfrac {2}{4}}-\color {Red}{\tfrac {2}{5}}\\1/\Delta _{5}&={\tfrac {1}{15}}&=\color {Red}{\tfrac {2}{5}}-\color {Red}{\tfrac {2}{6}}\\1/\Delta _{6}&={\tfrac {1}{21}}&=\color {Red}{\tfrac {2}{6}}-\color {Red}{\tfrac {2}{7}}\\&\qquad \vdots &\qquad \vdots \end{aligned}}

\sum _{i=1}^{n}{\frac {1}{\Delta _{i}}}=\left({\frac {2}{1}}-{\frac {2}{2}}\right)+\left({\frac {2}{2}}-{\frac {2}{3}}\right)+\left({\frac {2}{3}}-{\frac {2}{4}}\right)+\dots +\left({\frac {2}{n-1}}-{\frac {2}{n}}\right)+\left({\frac {2}{n}}-{\frac {2}{n+1}}\right)={\frac {2}{1}}-0-0-\dots -0-{\frac {2}{n+1}}=2-{\frac {2}{n+1}}={\frac {2n}{n+1}}

\sum _{n=1}^{\infty }{\frac {1}{\Delta _{n}}}={\frac {1}{1}}+{\frac {1}{3}}+{\frac {1}{6}}+{\frac {1}{10}}+{\frac {1}{15}}+{\frac {1}{21}}+\dots =2

Dreieckswurzel

Analog zur Quadratwurzel bei der Quadratzahl lässt sich auch mit der Dreieckswurzel n die Seitenlänge einer Dreieckszahl $\Delta$ bestimmen:

n={\frac {{\sqrt {8\Delta +1}}-1}{2}}.

So wird z. B. die Dreieckszahl $\Delta _{4}=10$ aus $n=4$ Reihen gebildet.

Mit Hilfe der Dreieckswurzel lässt sich die Cantorsche Paarungsfunktion umkehren.

Diverses

Irene Schramm-Biermann. Serie Sichtbare Mathematik. Visualisierung von Dreieckszahlen und deren Berechnung mit Hilfe der Gaußschen Summenformel

Die zehnte, hundertste, tausendste, zehntausendste usw. Dreieckszahl ist 55, 5.050, 500.500, 50.005.000 usw. (OEIS, A037156).

Allgemein gilt

\Delta _{10^{n}}={\frac {10^{2n}+10^{n}}{2}}=5\cdot (10^{2n-1}+10^{n-1}).

Die Dreiecksfolgen zerfallen in zwei Teilfolgen. Die Glieder der Folge 3, 10, 21, 36, 55, 78, … (OEIS, A014105) lassen sich über die Formel $n\cdot (2n+1)$ bilden (siehe auch Sophie-Germain-Primzahl). Für die andere Hälfte, die Sechseckszahlen 1, 6, 15, 28, 45, 66, … (OEIS, A000384), gilt die Bildungsregel $n\cdot (2n-1)$ .
Der puerto-ricanische Mathematiker Pedro Antonio Pizá fand 1950 die Beziehung

3\cdot \left(\sum _{k=1}^{n}\Delta _{k}\right)^{3}=\sum _{k=1}^{n}\Delta _{k}^{3}+2\cdot \sum _{k=1}^{n}\Delta _{k}^{4}={\frac {1}{72}}n^{3}(n+1)^{3}(n+2)^{3}

zwischen Summen und Potenzen von Dreieckszahlen.[6]

Die Anzahl der Diagonalen im konvexen $n$ -Eck beträgt $\Delta _{n-2}-1={\frac {n(n-3)}{2}}$ .
Die Folge der zentralpolygonalen Zahlen (auch als Zahlenfolge des faulen Kellners bezeichnet) erhält man, indem man zu den Dreieckszahlen jeweils die Zahl 1 addiert.
Für die Abrundungsfunktion gilt: $\lfloor 2{\sqrt {\Delta _{n}}}\rfloor =\lfloor (n+{\frac {1}{2}}){\sqrt {2}}\rfloor$ .
Der Modulrest ist alternierend in n: $T(n)\equiv \{(r+1)/2+\lfloor {r^{2}/2}\rfloor ,T(r+1)\}\mod {n+r},0\leq (r-1)^{2}+1\leq n$ wenn n {ungerade,gerade} ist und r ungerade, aber $T(n)\equiv \{T(r+1),r/2+\lfloor {r^{2}/2}\rfloor \}\mod {n+r},0\leq (r-1)^{2}+1\leq n$ wenn r gerade ist.
Visualisierung für Tripel(2,2,3)
Für alle $a>1$ , aber nur für bestimmte Tripel $(a,b,c)$ mit $1<a\leq b<c$ gilt $\Delta _{a}+\Delta _{b}=\Delta _{c}$ (OEIS, A012132); für stumpfwinkelige Dreiecke (a,b,c) gilt: $\csc(\phi )=1+a+b+c=-{\frac {2ab}{a^{2}+b^{2}-c^{2}}}$ ; für spitzwinkelige Dreiecke (a+1,b+1,c+1) gilt: $\csc(\phi )=(-1)+(a+1)+(b+1)+(c+1)={\frac {2(a+1)(b+1)}{(a+1)^{2}+(b+1)^{2}-(c+1)^{2}}}$ . Dies gilt auch mit reellen Strecken, $a(a+1)+b(b+1)=c(c+1),a+b-c\neq 0$ , bspw. ganzzahlig: (-1, -1, -1), (-2, -1, 1), (-1, 1, 1), (2, 2, 3), da diese Strecken die Elemente eines Hilbert-Raums sind.

Verallgemeinerungen

siehe Hauptartikel: Polygonalzahl, reguläre figurierte Zahl

Es gibt im Wesentlichen zwei Verallgemeinerungen der Dreieckszahlen. Bleibt man in der Ebene, dann kann man das Konstruktionsprinzip der Dreieckszahlen auf Polygone mit mehr Ecken anwenden. Dadurch entstehen die Polygonalzahlen, zu denen beispielsweise die Quadratzahlen und die Fünfeckszahlen zählen.

Die zweite Verallgemeinerung besteht darin, die Ebene zu verlassen und zu höheren Dimensionen überzugehen. Im Dreidimensionalen betrachtet man dann einen Tetraeder, das ist eine Pyramide mit gleichseitigen Dreiecken als Seiten. Im Vierdimensionalen gelangt man zum Pentatop, dessen Seiten Tetraeder sind. Dies lässt sich beliebig fortsetzen. Die zugehörigen figurierten Zahlen heißen Tetraederzahlen, Pentatopzahlen und im allgemeinen Fall reguläre figurierte Zahlen. Im Eindimensionalen sind noch die natürlichen Zahlen zu erwähnen.

Für Dreieckszahlen $\Delta _{n}\geq 6$ gilt die Bildungsvorschrift genau einer von drei disjunkten Zahlenklassen (Folge A111774 in OEIS)

\Delta _{n}={\frac {n\cdot (n+2k-1)}{2}};k\geq 1,n\geq 3

für den Sonderfall $k=1$ .

Siehe auch

Literatur

John H. Conway, Richard K. Guy: The Book of Numbers. Copernicus, New York NY 1996, ISBN 0-387-97993-X.

Weblinks

Commons: Dreieckszahlen – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Dreieckszahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Leonard Eugene Dickson: History of the Theory of Numbers. Volume 2: Diophantine Analysis. Dover Publications, Mineola NY 2005, ISBN 0-486-44233-0, S. 1.
Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 116
Hubert Mania: Gauß. Eine Biographie. Rowohlt, Reinbek bei Hamburg 2008, ISBN 978-3-498-04506-7, S. 108.
Leonard Eugene Dickson: History of the Theory of Numbers. Volume 2: Diophantine Analysis. Dover Publications, Mineola NY 2005, ISBN 0-486-44233-0, S. 2
Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 191
Pedro Antonio Pizá: Sums of Powers of triangular numbers. In: Scripta Mathematica 16 (1950), S. 127.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Leonard Eugene Dickson: History of the Theory of Numbers. Volume 2: Diophantine Analysis. Dover Publications, Mineola NY 2005, ISBN 0-486-44233-0, S. 1.

[2] Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 116

[3] Hubert Mania: Gauß. Eine Biographie. Rowohlt, Reinbek bei Hamburg 2008, ISBN 978-3-498-04506-7, S. 108.

[4] Leonard Eugene Dickson: History of the Theory of Numbers. Volume 2: Diophantine Analysis. Dover Publications, Mineola NY 2005, ISBN 0-486-44233-0, S. 2

[5] Roger B. Nelsen: Beweise ohne Worte, Deutschsprachige Ausgabe herausgegeben von Nicola Oswald, Springer Spektrum, Springer-Verlag Berlin Heidelberg 2016, ISBN 978-3-662-50330-0, Seite 191

[6] Pedro Antonio Pizá: Sums of Powers of triangular numbers. In: Scripta Mathematica 16 (1950), S. 127.