Cyclovoltammetrie

Die Cyclovoltammetrie, auch zyklische Voltammetrie oder Dreieckspannungsmethode genanntes analytisches Verfahren, mit dem man verschiedene Elektrodenprozesse untersuchen kann.

Abbildung 1: Potential und Stromdichte in einem reversiblen elektrochemischen Redox Experiment (Graphit Stabelektrode in 5mM Fe Spezies mit 1 M Kaliumnitrat im Hintergrund). Ein Vergleich mit dem Elektrolyten im Hintergrund ohne redoxaktive Spezies findet sich hier .

Bei der zyklischen Voltammetrie wird an die Arbeitselektrode in einem Elektrolyten erst ein linear ansteigendes oder abfallendes und anschließend ein rückläufiges Potential angelegt. Von diesem dreieckförmigen Spannungsverlauf kommt die Bezeichnung Dreieckspannungsmethode.

Wenn sich an der Arbeitselektrode ein elektrochemisch aktiver Stoff befindet, wird dieser bei einem charakteristischen Potential oxidiert oder reduziert, siehe Abbildung 1. Der Spannungswert zwischen dem Oxidations- und dem Reduktionspeak gibt das Normalpotential einer elektrolytischen Reaktion an und somit Rückschluss auf die enthaltenen Spezies. Neben der Stoffidentifikation in der analytischen Chemie ist die Cyclovoltammetrie eine wichtige Methode zur Charakterisierung von elektrochemischen Katalysatoren.

Bei den so genannten CV oder Cyclovoltammogrammen (in der älteren Literatur "Zyklovoltammogrammen") wird dann die Stromdichte gegen das Elektrodenpotential aufgetragen. Für eine reversible Redoxreaktion wie oben ergibt sich dann die Auftragung wie in Abbildung 2.

Abbildung 2. Typisches Cyclovoltammogram generiert aus den Zeitverläufen in Abbildung 1. j_PA und j_PC zeigen die anodische bzw. kathodische Peakstromdichte einer reversiblen Redoxreaktion. E_PA und E_PC sind die dazugehörigen Peakpotentiale.

Funktionsweise

Experimenteller Aufbau

Experimenteller Aufbau: Der Potentiostat hält die Spannung zwischen Arbeits- und Referenzelektrode konstant auf U0, indem er einen Strom zwischen Arbeits- und Gegenelektrode treibt.

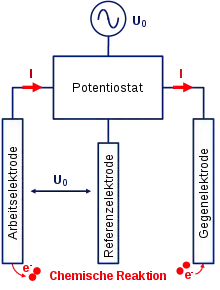
Die Cyclovoltammetrie wird üblicherweise mit drei Elektroden, die in einem ionenleitenden Elektrolyten eingetaucht sind, durchgeführt. An der Arbeitselektrode finden die zu untersuchenden elektrochemischen Prozesse bei einem gegebenen Potential statt. Das Potential der Arbeitselektrode wird mittels einer sogenannten Referenzelektrode genau bestimmt. Der Strom zum Aufbau der Spannung, welcher den elektrochemischen Prozessen entspricht, wird mithilfe der Gegenelektrode bereitgestellt. Ein Potentiostat verbindet die drei Elektroden und sorgt für die Spannungssteuerung und Strommessung. Zwischen dem Potentiostaten und den elektrisch leitenden Elektroden fließen Elektronen. Im Elektrolyten hingegen liegt eine reine ionische Leitfähigkeit vor.

Messablauf

Ausgehend vom Startpotential, wofür oftmals die Leerlaufspannung (engl. open circuit potential, OCP) gewählt wird, wird eine Dreiecksspannung abgefahren. Dieser Spannungsverlauf wird definiert durch zwei Umkehrpotentiale und die Frequenz (auch als Vorschubgeschwindigkeit des Potentials bezeichnet). Je nach Polarität der Spannung an der Arbeitselektrode wird diese im positiven Fall zur Anode und bei negativen Potentialen zur Kathode. Die Umkehrpotentiale können entsprechend als kathodisches beziehungsweise anodisches Umkehrpotential bezeichnet werden. Der fließende Strom wird in Abhängigkeit von der Spannung aufgezeichnet. Um die zeitliche Abhängigkeit der ablaufenden Prozesse zu untersuchen, werden oft mehrere Messungen unmittelbar hintereinander durchgeführt. Unter Verwendung dieser Ergebnisse können dann weitere Experimente folgen. So kann dann bei einem bestimmten Potential eine Wechselspannung überlagert werden und so eine Impedanz bestimmt werden.

Abbildung 3: Zyklovoltammogramme des oben beschriebenen Redoxsystems über einen weiten Bereich von Vorschubgeschwindigkeiten. Dieses Experiment nur mit dem Hintergrundelektrolyten ohne redoxaktive Spezies findet sich hier.

Interpretation

Grundsätzlich lässt sich die erhaltene Stromantwort in zwei Beiträge unterteilen: Der kapazitive Strom entsteht durch eine Änderung des Elektrodenpotentials und der damit verbundenen Neuordnung der elektrochemischen Doppelschicht. Er ist unabhängig vom Elektrodenpotential und entspricht in erster Näherung der Ladung bzw. Entladung eines klassischen Plattenkondensators. Der faradaysche Strom entsteht durch die elektrochemische Oxidation oder Reduktion einer chemischen Spezies und ist somit abhängig vom Elektrodenpotential. Bei höheren Messfrequenzen der Dreiecksspannung wird der kapazitive Strom prominenter.

Bei einem gewissen positiven Potential setzt ein faradayscher Stromfluss ein. Direkt an der Oberfläche der Elektrode werden nun Teilchen oxidiert (z. B. Fe²⁺ zu Fe³⁺). Dabei ändert sich sofort das Verhältnis von oxidierten zu reduzierten Teilchen direkt vor der Elektrode nach der Nernstgleichung. Wenn die Konzentration der oxidierten und reduzierten Komponenten vor der Elektrode gleich ist, entspricht das Potential idealerweise dem Standardpotential eines Redoxprozesses der Nernstgleichung. In der Realität sind die Peaks gegenüber dem Standardredoxpotential verschoben, da für die Teilprozesse des Elektronentransfers eine gewisse Überspannung benötigt wird. Deshalb liegen Oxidations- und Reduktionspeak nicht direkt übereinander. Der Mittelwert der beiden Peaks entspricht dem Standardredoxpotential. Nur bei einer reversiblen Reaktion können sowohl Oxidations- und Reduktionspeak beobachtet werden.

Je nach Frequenz der Dreiecksspannung ist der Stofftransport zur Elektrode limitierend. Es bildet sich nach kurzer Zeit eine Verarmungszone an der Elektrodenoberfläche aus, welche eine geringere Stoffumsetzung und somit einen geringeren Strom bedeutet. Dieses Absinken des Stroms führt zur Ausbildung von Peaks im Voltammogramm (Abhängigkeit: Quadratwurzel der Zeit). Der Nachtransport der Redox-Spezies ist durch die Diffusion limitiert. Daraus resultiert auch die Diffusionsüberspannung.

Wichtig ist auch, zu wissen, wo das Voltammogramm aufgenommen wurde. So ist die Potential-Achse nach IUPAC und Amerika invertiert. Weitere Unterschiede können im Paper von Elgrishi nachgelesen werden.[1]

Theoretische Beschreibung

Im Cyclovoltammogramm tritt dann ein Peak (engl. Höchstwert, Spitze) auf, den man als Überlagerung einer Stufenkurve (wie sie in der Polarografie auftritt) und einer Stromverlaufskurve einer diffusionskontrollierten Elektrodenreaktion (Cottrell-Kurve) interpretieren kann. Die genaue Form dieser Kurve hängt auch von der Vorschubgeschwindigkeit des Potentials (Frequenz der Dreiecksspannung) ab. Aber auch ohne elektroaktive Spezies kann die elektrochemische Reaktion der (oft aus einem Metall bestehenden) Elektrode mit dem Lösungsmittel, zum Beispiel die Oxidation zu einem Peak führen, des Weiteren können ebenfalls Adsorptionsprozesse an der Messelektrode zu Peaks führen („Deckschichtdiagramm“).

Bei einem reversiblen Elektrodenprozess ist das Potential an der Elektrodenoberfläche durch die Nernst-Gleichung bestimmt. Wegen der Diffusionskontrolle gilt das 1. Ficksche Gesetz. Daraus kann die Stromdichte $i_{P}$ berechnet werden. Die entsprechende Randles-Sevčik-Gleichung lautet für den anodischen Halbzyklus:

i_{P}=2,69\cdot 10^{5}\cdot c_{\mathrm {red} }\,{\sqrt {n^{3}\cdot \nu \cdot D_{\mathrm {red} }}}

n

: Anzahl der Elektronen

\nu

: Vorschubgeschwindigkeit des Potentials (meist mV/s)

D_{\mathrm {red} }

: Diffusionskoeffizient der reduzierten Form des untersuchten Stoffes

c_{\mathrm {red} }

: Konzentration dieses Stoffes

Für den kathodischen Halbzyklus gilt eine entsprechende Formel.

Eine genaue quantitative Erfassung der Messung ist auch möglich, wobei sich je nach Art der Elektrodenprozesse (reversibel oder irreversibel) verschiedene mathematische Ausdrücke ergeben. Allerdings können auch beide kombiniert auftreten.

Mit Hilfe der Cyclovoltammetrie kann man die Kinetik einer chemischen Reaktion aufklären. Normalerweise bedient man sich dabei bestimmter Diagnosekriterien, die für verschiedene Reaktionsmechanismen charakteristisch sind.

Neben Redoxreaktionen lassen sich bei geeigneter Reaktionsführung auch weitere reversible und irreversible Prozesse in einem cyclovoltammetrischen Experiment beobachten, etwa das Aufladen der Doppelschichtkapazität C, für das sich die Stromdichte j errechnet zu j = − ν C.

Abgeleitete Methoden

Um die Effekte des Massentransportes untersuchen zu können, kann die Arbeitselektrode in Rotation versetzt werden. Siehe Rotierende Scheibenelektrode.
An der Arbeitselektrode stattfindende Prozesse können mit Hilfe des elektrochemischen Rastertunnelmikroskops während des Ablaufes der Cyclovoltammetrie beobachtet werden.

Literatur

J. Heinze: Cyclovoltammetrie – die „Spektroskopie“ des Elektrochemikers. In: Angewandte Chemie. Band 96, 1984, S. 823–840, doi:10.1002/ange.19840961104.
Bernd Speiser: Cyclische Voltammetrie, Chemie in unserer Zeit 15. Jahrgang, April 1981, Seite 62–67, doi:10.1002/ciuz.19810150206
Allen J. Bard & Larry R. Faulkner: Electrochemical Methods: Fundamentals and Applications, 2nd Edition. Wiley, New York 2001, ISBN 978-0-471-04372-0.
Piero Zanello: Inorganic Electrochemistry: Theory, Practice and Application, 2nd Edition. RSC Publishing, 2011, ISBN 978-1-84973-071-6.
N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart, J. L. Dempsey: A Practical Beginner’s Guide to Cyclic Voltammetry. In Journal of Chemical Education. Band 95, 2017, S. 197–206, doi:10.1021/acs.jchemed.7b00361

Weblinks

Cyclovoltammetrie von der TU Clausthal (PDF; 153 kB)

Einzelnachweise

Noémie Elgrishi: A Practical Beginner’s Guide to Cyclic Voltammetry. In: Journal of Chemical Education. 95. Jahrgang, 2018, S. 197–206, doi:10.1021/acs.jchemed.7b00361 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Noémie Elgrishi: A Practical Beginner’s Guide to Cyclic Voltammetry. In: Journal of Chemical Education. 95. Jahrgang, 2018, S. 197–206, doi:10.1021/acs.jchemed.7b00361 (englisch).