Bialgebra

Sei ${\displaystyle k}$ ein Körper und ${\displaystyle B}$ sowohl unitäre assoziative Algebra über ${\displaystyle k}$ als auch Koalgebra über ${\displaystyle k}$. Dabei bezeichne ${\displaystyle \mu _{B}}$ die Multiplikation, ${\displaystyle \eta _{B}}$ die Eins (Einbettung des Körpers in die Algebra), ${\displaystyle \Delta _{B}}$ die Komultiplikation und ${\displaystyle \epsilon _{B}}$ die Koeins.

${\displaystyle B}$ heißt Bialgebra über ${\displaystyle k}$ wenn die folgenden äquivalenten Kompatibilitätsbedingungen erfüllt sind.

• Die Komultiplikation ${\displaystyle \Delta _{B}}$ und die Koeins ${\displaystyle \epsilon _{B}}$ sind Algebrahomomorphismen.
• Die Multiplikation ${\displaystyle \mu _{B}}$ und die Eins ${\displaystyle \eta _{B}}$ sind Koalgebrahomomorphismen.
• Die folgenden Diagramme kommutieren

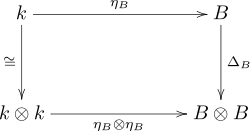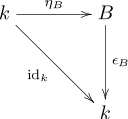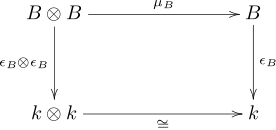Dabei ist ${\displaystyle \tau _{B,B}:=v\otimes w\mapsto w\otimes v}$ die „Flip“-Abbildung, also der kanonische Isomorphismus der Tensorprodukte ${\displaystyle V\otimes W}$ und ${\displaystyle W\otimes V}$ angewandt auf ${\displaystyle B\otimes B}$.

Die Bialgebren bilden zusammen mit den Abbildungen, die sowohl Algebra- als auch Koalgebrahomomorphismen sind, eine Kategorie.

Algebren und Koalgebren können in beliebigen monoidalen Kategorien betrachtet werden. Für Kompatibilitätsbedingungen ist es jedoch notwendig, dass auch das Tensorprodukt einer (Ko-)Algebra auf natürliche Weise wieder eine (Ko-)Algebra ist, dies bedingt die Existenz einer Zopfung.

• Christian Kassel: Quantum Groups (Graduate Texts in Mathematics). Springer-Verlag, ISBN 0-387-94370-6