Armillarsphäre

Armillarsphären im manuelinischen Portal des Rathauses von Olivenza, Provinz Badajoz

Der gedachte Beobachter befindet sich im Mittelpunkt der Kugel. Wenn das Gerät das geozentrische Weltbild abbilden soll, befindet sich dort im Zentrum der Armillarsphäre die Erde. Solche Armillarsphären sind bereits in primitiven Versionen für das alte Babylonien nachgewiesen. Das kopernikanische Weltbild wird in der 1657 von Andreas Bösch geschaffenen Sphaera Copernicana dargestellt.

Als Armille wird ein der Armillarsphäre ähnliches astronomisches Winkelmessinstrument mit Absehen bezeichnet, mit dem Koordinaten an der Himmelskugel bestimmt und umgewandelt wurden. Es taugte auch zur genäherten Ortsbestimmung und Zeitmessung[1] und wurde von Eratosthenes noch unter der Bezeichnung Astrolabium eingeführt. Ptolemäus beschreibt in Kapitel 5,1 seines Hauptwerkes Almagest den Bau einer Armillarsphäre. Das Instrument blieb über das gesamte Mittelalter hauptsächlich im islamischen Raum in Gebrauch. In Mitteleuropa wurde sie erst Mitte des 15. Jahrhunderts durch den fränkischen Astronomen Regiomontanus wieder bekannt und erreichte Ende des 16. Jahrhunderts mit dem dänischen Astronomen Tycho Brahe ihre Perfektionierung, der ebenso das Gerät ersann, das sie als präzises Positionsmessinstrument ersetzte: den Mauerquadranten.

Nach der Einführung des Teleskops in die Astronomie durch Thomas Harriot, Galileo Galilei, Simon Marius und andere zu Beginn des 17. Jahrhunderts trat die Armillarsphäre als Beobachtungsinstrument allmählich in den Hintergrund, da sie aufgrund ihrer Bauweise nur schlecht mit einem Teleskop bestückt werden konnte – anders als ein Quadrant, der dafür wesentlich besser geeignet ist. In den folgenden Jahrhunderten wurde die Armillarsphäre zu einem Gegenstand künstlerischer Darstellung und zu einem reinen Symbol der Astronomie.

Eine Armillarsphäre ist zum Beispiel ist als Zeichen für die große Verbundenheit Portugals mit der Seefahrt auf der portugiesischen Nationalflagge abgebildet.

Anhand einer Armillarsphäre können gleichzeitig drei geozentrische astronomische Koordinatensysteme veranschaulicht werden:

• das horizontale Koordinatensystem mit Azimut und Höhenwinkel sowie mit Zenit und Nadir
• das äquatoriale Koordinatensystem mit Deklination und Stundenwinkel sowie den beiden Himmelspolen und den beiden Coluren
• das ekliptikale Koordinatensystem mit ekliptikaler Länge und ekliptikaler Breite

• 
  Armillarsphäre zur Winkelmessung
• 
  Armillarsphäre im Stadtmuseum Göttingen
• 
  Armillarsphäre im Ariana-Park, Genf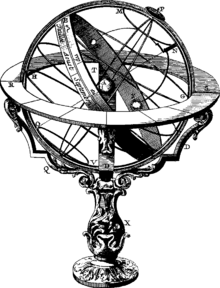
• 
  Darstellende Armillarsphäre
• 
  Armillarsphäre aus einem Gemälde Botticellis
• 
  Ehrengrab Vasco da Gamas, Hieronymitenkloster, Lissabon

Armillarsphäre

Das Bild rechts zeigt eine Armillarsphäre, die oben an einer Öse aufgehängt wird. Im Bild ist die Öse auf 50 Bogengrad Nord eingestellt. Lässt sie sich verschieben, kann die Armillarsphäre an den Standort des Benutzers angepasst werden. Dazu muss auch die Scheibe „Horizont“ justiert werden. Der Beobachter selbst befindet sich gedanklich im Mittelpunkt der Erde innerhalb der Armillarsphäre. Der Horizont des Beobachters liegt immer waagerecht.

Der Himmel oberhalb des Horizonts ist sichtbar, die darunter liegenden Bereiche werden von der Erdoberfläche verdeckt. Die inneren Ringe bilden die Himmelskugel, die in der Himmelsachse (identisch mit Erdachse) gegenüber dem Horizont und dem Meridian drehbar gelagert ist. Wäre die Himmelskugel ganz ausgeführt, so könnte man von außen die Sterne auftragen, hätte aber keinen Zugang zum Inneren der Kugel. Aus diesem Grund wird die Himmelskugel lediglich mit dem Himmelsäquator und einigen Parallelkreisen zu ihm angedeutet. Die Ekliptik beschreibt mit ihrer Neigung von 23,5 Bogengrad gegenüber dem Himmelsäquator den Verlauf der Sonne.

Bei vielen Modellen wird die Sonne als kleine Kugel auf den Ekliptikring gesetzt. Eine Umdrehung des Himmels lässt die Sonne über den Horizont auf- und untergehen. Die Dauer der Dämmerung und der maximale Sonnenstand hängen davon ab, wo sich die Sonne auf der Ekliptik gerade aufhält. Befindet sie sich beispielsweise im Bild oben rechts, dann zeigt die Armillarsphäre ihren Höchststand im Juni zur Mittagszeit an. Steht sie hingegen links unten auf der Ekliptik, hat die Sonne ihren Tiefststand im Dezember, es ist Mitternacht. Dreht sich die Himmelskugel um die Erdachse, steigt die Wintersonne mittags nur wenig über den Horizont.

Neben der Sonne erhält oft auch der Mond einen eigenen Ring. Dieser ist um gut 5 Bogengrad gegenüber der Ekliptik geneigt. Die Planeten finden ohne allzu große Fehler ihren Platz auf der Ekliptik.

• Friedrich Nolte: Die Armillarsphäre. Mencke, Erlangen 1922 (Abhandlungen zur Geschichte der Naturwissenschaften und der Medizin. 2, ZDB-ID 537096-6), (Philosophische Dissertation, Erlangen 1922).
• Peter E. Allmayer-Beck (Hrsg.): Modelle der Welt. Erd- und Himmelsgloben. Brandstätter, Wien 1997, ISBN 3-85447-733-3.

Wiktionary: Armillarsphäre – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Armillarsphäre – Album mit Bildern, Videos und Audiodateien

• Literatur von und über Armillarsphäre im Katalog der Deutschen Nationalbibliothek
• Astronomische Instrumente Tycho Brahes, darunter drei messende Armillarsphären verschiedener Bauart
• Kurze Dokumentation zur Geschichte und Verwendung sowie eine 3D-Animation (Quicktime)
• Dokumentation und Erklärung einer neu gestalteten Armillarsphäre
• Detaillierte Informationen zur Geschichte und Funktionsweise mit vielen hochwertigen Bildern

1. Ralf Kern. Wissenschaftliche Instrumente in ihrer Zeit. Band 1: Vom Astrolab zum mathematischen Besteck. Köln, 2010. S. 227.