Antiparallelogramm

Als Antiparallelogramm wird ein sich selbstüberschneidendes Viereck bezeichnet, dessen jeweils gegenüberliegende, also nicht benachbarte Seiten die gleiche Länge besitzen und bei dem sich (im Gegensatz zu einem gewöhnlichen Parallelogramm) zwei Seiten schneiden und nicht parallel liegen.[1] Insbesondere ist es nicht konvex. Manchmal wird von einem Antiparallelogramm zusätzlich gefordert, dass ein Paar gegenüberliegender Seiten parallel sein soll.

Ein Antiparallelogramm

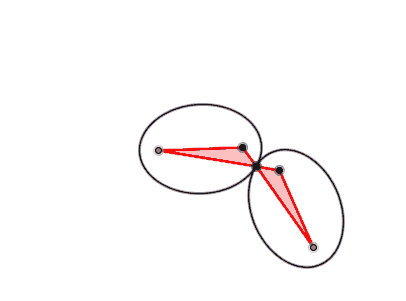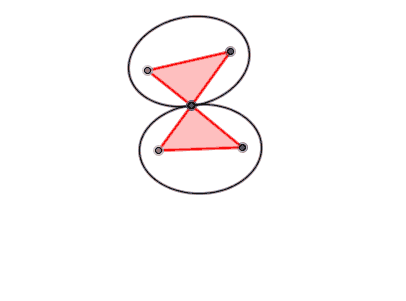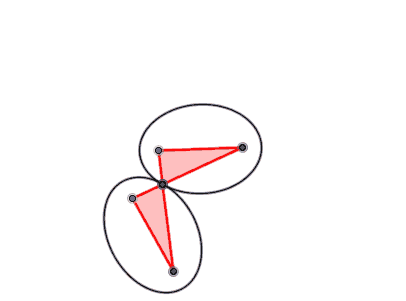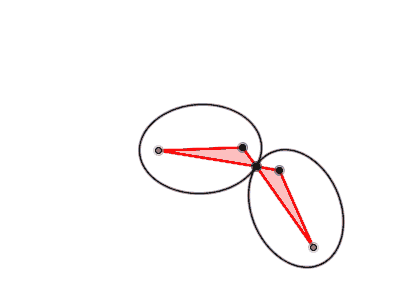
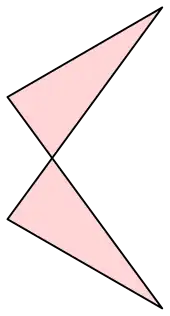
Stehen die Längen der benachbarten Seiten eines Antiparallelogramms im Verhältnis und hält man eine der beiden längeren Seiten fest, dann beschreibt der Mittelpunkt der gegenüberliegenden Seite eine Bernoullische Lemniskate.

Baut man ein Antiparallelogramm als Koppelgetriebe mit starren Seiten und Gelenken an den Eckpunkten auf, dann kann man damit geradlinige Bewegungen in kreisförmige umwandeln, also einen Ersatz für ein Pleuel schaffen.[2] (Siehe hierzu auch Inversor von Hart)

Literatur
  • Harold Scott MacDonald Coxeter, Michael S. Longuet-Higgins, J. C. P. Miller: Uniform polyhedra. In: Philosophical Transactions of the Royal Society of London (= A. Mathematical and Physical Sciences). Band 246, 1954, S. 401–450, doi:10.1098/rsta.1954.0003.
  • Norbert Treitz: Das Antiparallelogramm (I). In: Spektrum der Wissenschaft. April 2006, S. 114–116 (spektrum.de [abgerufen am 4. Juni 2013]).
  • John Briant, Christopher J. Sangwin: How round is your circle? Where Engineering and Mathematics Meet. Princeton University Pres, 2008, ISBN 978-0-691-13118-4, S. 54–56 (online auf google-books [abgerufen am 4. Juni 2013]).
  • E. A. Dijksman: Motion Geometry of Mechanisms. Cambridge University Press, 1976, ISBN 978-0-521-20841-3, S. 203 f. (online auf google-books [abgerufen am 4. Juni 2013]).
Commons: Antiparallelogramm – Sammlung von Bildern, Videos und Audiodateien
  • Das Online-Lexikon Academic dictionaries and encyclopedias definiert ein Antiparallelogramm als „ein Viereck, in welchem das eine Paar der Gegenseiten parallel, aber ungleich, das andere gleich, aber nicht parallel ist.“ Dem vorliegenden Artikel liegt die Definition zugrunde, die in der weiter oben genannten Literatur verwendet wird.
  • Spektrum der Wissenschaft zeigt:
Rollende Ellipsen, Das Antiparallelogramm, Harts Inversor, Das Antiparallelogramm (II)

Einzelnachweise
  1. Treitz (2006)
  2. Briant, Sangwin (2008)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.