Helmholtz-Spule
Als Helmholtz-Spule bezeichnet man eine besondere Anordnung von Magnetspulen, die auf den deutschen Physiker Hermann von Helmholtz (1821–1894) zurückgeht: Zwei kurze kreisförmige Spulen mit großem Radius R werden im Abstand R auf derselben Achse parallel aufgestellt und gleichsinnig von Strom durchflossen (bei gegensinnigem Stromfluss siehe Anti-Helmholtz-Spule).

Das Feld einer einzelnen Spule ist inhomogen. In der geometrischen Anordnung der Helmholtz-Spulen überlagern sich die Felder beider Spulen aber gerade so, dass sich zwischen ihnen nahe der Spulenachse ein Bereich mit weitgehend homogenem Magnetfeld ergibt, das für Experimente frei zugänglich ist.
Es gibt Helmholtz-Spulen in verschiedenen Bauformen: zylindrisch, quadratisch, aber auch als 3 orthogonal aufgestellte Paare (dreidimensional). Mit der dreidimensionalen Anordnung kann man durch Variation des Stromverhältnisses zwischen den Spulenpaaren ein Magnetfeld beliebiger Richtung erzeugen und damit einen Gegenstand untersuchen, ohne diesen drehen zu müssen.
Eigenschaften
Bei der Anordnung nach Helmholtz verschwinden in der Mitte die erste, zweite und dritte Ableitung der Feldfunktion in alle Richtungen, am Rand fällt die Feldstärke relativ schnell ab. Die Helmholtz-Spule ist damit die einfachste Spulenanordnung um ein nahezu konstantes Magnetfeld innerhalb eines endlichen Volumens zu erzeugen und wird häufig in physikalischen Experimenten verwendet. Die erzeugte magnetische Feldstärke ist – wie bei jeder Luftspule – streng linear vom Spulenstrom abhängig. Aus der Spulengeometrie, dem Strom und den Windungszahlen lässt sich die magnetische Feldstärke entlang der Achse analytisch berechnen. Daher ist die Helmholtz-Spule ideal für die Kalibrierung von Magnetometern einsetzbar.
Größere Abstände als der Spulenradius R ergeben ein größeres Experimentiervolumen, aber zur Spulenmitte hin abfallende Feldstärkewerte. Kleinere Abstände ergeben größere Feldstärken, aber ein kleineres Experimentiervolumen.
Anwendungen

- Bestimmung der spezifischen Elektronenladung nach Helmholtz mit Fadenstrahlrohr
- Qualitätskontrolle von Dauermagneten
- Hall-Effekt-Untersuchungen
- Herstellung feldfreier Räume durch gezielte Abschirmung des Erdmagnetfelds
- Kalibrierung von Magnetfeldsonden und Magnetometern
- Hochfrequenz-Spule für die Magnetresonanztomographie (MRT)
- Gradientenspule (Maxwell-Spule, s. unten) für die MRT
- Magnetfeldtherapie (bewiesen unwirksame, angebliche Behandlungsmethode)
Berechnung der magnetischen Flussdichte

Die magnetische Flussdichte einer Helmholtz-Spule ergibt sich als Summe der Flussdichten der beiden kreisförmigen Leiterschleifen. Diese sind durch das Biot-Savart-Gesetz berechenbar, was aber im Allgemeinen auf analytisch nicht lösbare elliptische Integrale führt. Auf der Symmetrieachse (z-Achse) beträgt das Feld einer einzelnen Leiterschleife, die um zentriert ist,
wobei die magnetische Feldkonstante, der Spulenradius und die Spulenstromstärke ist. Das gesamte Feld eines Spulenpaares mit gleichsinnigen Strömen und Spulenabstand beträgt daher
- , wobei die Windungszahl je Spule ist.
Die Flussdichte im Zentrum der Anordnung bei ist aufgrund der Spulensymmetrie eine gerade Funktion, das heißt, dass alle Ableitungen ungerader Ordnung nach dort verschwinden. Insbesondere ist das Feld dort für beliebige Spulenabstände in linearer Näherung konstant. Die Helmholtz-Spule ist der spezielle Fall mit einer maximal homogenen Flussdichte im Zentrum der Anordnung, bei dem auch noch die zweite Ableitung verschwindet,
- .
Diese Bedingung ist erfüllt für
- ,
also wenn der Abstand genau dem Radius entspricht. Um das Zentrum herum variiert die Feldstärke dann nur in vierter Ordnung .
Die Flussdichte im Zentrum beträgt:
Eine Helmholtz-Spule mit und erzeugt beispielsweise eine zentrale Flussdichte von .
Induktivität
Für die beiden in Reihe geschalteten Spulenteile ergibt sich aufgrund der symmetrischen Anordnung der Ansatz . Dabei ist die Selbstinduktivität einer einzelnen Teilspule. Die Gegeninduktivität ergibt sich aus der magnetischen Kopplung beider Spulenteile aufeinander und wirkt auf beide Spulenteile gleich.
Es handelt sich um kurze Zylinderspulen, deshalb gilt für die Selbstinduktivität die Näherungsformel
- .
ist die Länge einer Zylinderspule.
Die Gegeninduktivität lässt sich für die vorliegende Anordnung mit dem Neumann-Kurvenintegral berechnen. Nach der Integration ergibt sich die Formel
- .
Insgesamt hat eine Helmholtz-Spule also die Induktivität
- .
Bei einer Anti-Helmholtz-Spule ergibt sich die Induktivität aus dem Ansatz . Die Gegeninduktivität fließt negativ in die Gesamtinduktivität ein, da sich die Magnetfelder destruktiv überlagern. Insgesamt also:
Variationen und Weiterentwicklung
Quadratische Helmholtzspule
In der Praxis werden die runden Einzelspulen oft durch quadratische Leiterschleifen der Kantenlänge a ersetzt. Damit lassen sich ähnlich homogene Felder erzeugen. Der ideale Spulenabstand beträgt dann d=0,5445a[1][2], etwas größer als bei einer runden Helmholtzspule mit Durchmesser a, da die quadratische Spule auch eine größere Fläche besitzt.
Anordnungen für noch homogenere Felder
 Maxwell-Spule
Maxwell-Spule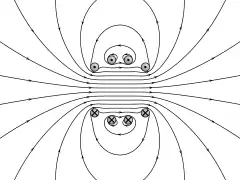 Braunbek-Spule
Braunbek-Spule Barker-Spule
Barker-Spule
Der Bereich homogenen Feldes ist im Vergleich zu den Gesamtabmessungen der klassischen Helmholtzspule klein. Daher versuchten viele Wissenschaftler, die Spulenanordnung zum Erzeugen homogener Felder zu verbessern. Es sind dies zum Beispiel:
- Maxwell-Spule[3]: drei Einzelspulen, wobei die mittlere Spule einen größeren Durchmesser hat und von einem größeren Strom durchflossen wird
- Braunbek-Spule[4]: vier Einzelspulen, wobei die inneren Spulen größere Durchmesser haben. Sie ist eine optimierte Version der Fanselau-Spule.[5]
- Barker-Spule[6]: vier Einzelspulen gleichen Durchmessers, wobei die äußeren von größerem Strom durchflossen werden
Diese Anordnungen verbessern das Verhältnis zwischen Gesamtgröße und Volumen homogenen Feldes und steigern dadurch auch die Effizienz, denn die Stromwege verkürzen sich. Die Barker-Spule wird in Kernspintomografen eingesetzt, die Braunbek-Spule in geomagnetischen Laboren zur Simulation und Kompensation des Erdmagnetfeldes und auch interplanetarer Felder, u. a. zum Test von Raumfahrzeugen. Weiterhin werden damit durch Kompensation äußerer Felder magnetfeldfreie Räume geschaffen, u. a. um Magnetometer zu testen.[7][8]
Anti-Helmholtz-Spule
Durchfließt der Strom die Spulen gegensinnig, so ist das Feld im Zentrum null. Im Bereich um das Zentrum steigt das Feld in Achsenrichtung linear an, so dass die Spulenanordnung ein Gradientenfeld erzeugt. Diese Spulenanordnung wird Maxwell-Spule, manchmal auch Anti-Helmholtz-Spule genannt. Der optimale Abstand d der Einzelspulen zueinander hängt von den gewünschten Feldeigenschaften ab: Ein maximaler Feldgradient im Zentrum ergibt sich beim Abstand , also genau wie bei der optimalen Helmholtz-Spule. Ein möglichst homogener Gradient, bei dem die zweite und dritte Ableitung der Feldstärke verschwindet, entsteht hingegen bei einem Spulenabstand , allerdings mit ca. 25 % verringerter Gradientenstärke.
Die Berechnung des Feldverlaufes entlang der Symmetrieachse (z-Achse) geschieht in ganz analoger Weise wie im Fall gleicher Richtung der Kreisströme. Man erhält für Spulenpaare mit gleicher Windungszahl N:
Mit Spulenabstand gilt dann für den Feldgradienten im Zentrum:
Mit Spulenabstand gilt entsprechend:
Bildgalerie
Nachfolgend sind gemessene oder errechnete Feldverläufe bei Helmholtz-Spulen dargestellt:
 Feldlinien
Feldlinien Spule im Labor
Spule im Labor Magnetfeld der Helmholtz-Spule mit Eisenfeilspänen sichtbar gemacht
Magnetfeld der Helmholtz-Spule mit Eisenfeilspänen sichtbar gemacht Berechnetes Magnetfeld der Helmholtz-Spule
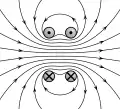
Berechnetes Magnetfeld der Helmholtz-Spule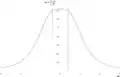 Magnetische Flussdichte entlang der Achse durch das Zentrum der Spulen; z=0 ist der Punkt in der Mitte zwischen den Spulen.
Magnetische Flussdichte entlang der Achse durch das Zentrum der Spulen; z=0 ist der Punkt in der Mitte zwischen den Spulen. Betrag der magnetischen Flussdichte als Funktion des Ortes. Die Schnittebene geht durch das Zentrum.
Betrag der magnetischen Flussdichte als Funktion des Ortes. Die Schnittebene geht durch das Zentrum.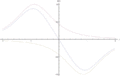 Maxwell-Spule: Feldstärkeverlauf bei optimiertem Spulenabstand von und Einzelfelder in willkürlichen Einheiten.
Maxwell-Spule: Feldstärkeverlauf bei optimiertem Spulenabstand von und Einzelfelder in willkürlichen Einheiten.
Weblinks
Einzelnachweise
- Carl Heller: Über die Erzeugung großräumiger homogener Magnetfelder zum Studium des Verhaltens von Magnetkompassen und Kompensiermitteln auf verschiedenen magnetischen Breiten. In: Deutsche Hydrografische Zeitschrift. 8. Jahrgang, Nr. 4, 1955, S. 157–164, doi:10.1007/BF02019812.
- James Clerk Maxwell: Treatise on Electricity and Magnetism. Band 2. The Clarendon Press, Oxford 1873, ISBN 0-486-60636-8, S. 320 (archive.org).
- Werner Braunbek: Die Erzeugung weitgehend homogener Magnetfelder durch Kreisströme. In: Zeitschrift für Physik. 88. Jahrgang, Nr. 5–6, 1934, S. 399–402, doi:10.1007/BF01343500.
- G. Fanselau: Die Erzeugung weitgehend homogener Magnetfelder durch Kreisströme. In: Zeitschrift für Physik. 54. Jahrgang, Nr. 3–4, 1929, S. 260–269, doi:10.1007/BF01339844.
- J. R. Barker: New Coil Systems for the Production of Uniform Magnetic Fields. In: Journal of Scientific Instruments. 26. Jahrgang, 1949, S. 273–275, doi:10.1088/0950-7671/26/8/307.
- serviciencia.es Prospekt der Fa. Serviciencia, S. L. / Spanien, abgerufen 2017-09-18
- igep.tu-bs.de 3D-Braunbek-Spulensystem in Magnetsrode - einem geomagnetischen Laboratorium