Algorithmus von Kruskal
Der Algorithmus von Kruskal ist ein Greedy-Algorithmus der Graphentheorie zur Berechnung minimaler Spannbäume von ungerichteten Graphen. Der Graph muss dazu zusätzlich zusammenhängend, kantengewichtet und endlich sein.
Der Algorithmus stammt von Joseph Kruskal, der ihn 1956 in der Zeitschrift „Proceedings of the American Mathematical Society“ veröffentlichte. Er beschrieb ihn dort wie folgt:
- Führe den folgenden Schritt so oft wie möglich aus: Wähle unter den noch nicht ausgewählten Kanten von (dem Graphen) die kürzeste Kante, die mit den schon gewählten Kanten keinen Kreis bildet.[1]
Die kürzeste Kante bezeichnet dabei jeweils die Kante mit dem kleinsten Kantengewicht. Nach Abschluss des Algorithmus bilden die ausgewählten Kanten einen minimalen Spannbaum des Graphen.
Wendet man den Algorithmus auf unzusammenhängende Graphen an, so berechnet er für jede Zusammenhangskomponente des Graphen einen minimalen Spannbaum. Diese Bäume bilden einen minimalen aufspannenden Wald.
Idee
Der Algorithmus von Kruskal nutzt die Kreiseigenschaft minimaler Spannbäume (englisch minimum spanning tree, MST). Dazu werden die Kanten in der ersten Phase aufsteigend nach ihrem Gewicht sortiert. In der zweiten Phase wird über die sortierten Kanten iteriert. Wenn eine Kante zwei Knoten verbindet, die noch nicht durch einen Pfad vorheriger Kanten verbunden sind, wird diese Kante zum MST hinzugenommen.
Beispiel
 |
Dies ist der Graph, zu dem nach dem Algorithmus von Kruskal ein minimaler Spannbaum berechnet wird. Die Zahlen bei den einzelnen Kanten geben das jeweilige Kantengewicht an. Zu Beginn ist noch keine Kante ausgewählt. |
 |
Die Kanten AD und CE sind die kürzesten (noch nicht ausgewählten) Kanten des Graphen. Beide können ausgewählt werden. Hier wird zufällig AD ausgewählt. (Dass diese keinen Kreis bildet, ist im ersten Schritt selbstverständlich.) |
 |
Nun ist CE die kürzeste, noch nicht ausgewählte Kante. Da sie mit AD keinen Kreis bildet, wird sie nun ausgewählt. |
 |
Die nächste Kante ist DF mit Länge 6. Sie bildet mit den schon gewählten Kanten keinen Kreis und wird deshalb ausgewählt. |
 |
Jetzt könnten die Kanten AB und BE, jeweils mit Länge 7, ausgewählt werden. Es wird zufällig AB gewählt. Die Kante BD wird rot markiert, da sie mit den bis jetzt gewählten Kanten einen Kreis bilden würde und somit im weiteren Verlauf des Algorithmus nicht mehr berücksichtigt werden muss. |
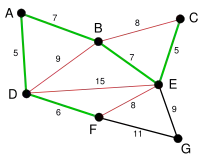 |
BE ist nun mit Länge 7 die kürzeste der noch nicht ausgewählten Kanten und da sie mit den bisher gewählten keinen Kreis bildet, wird sie ausgewählt. Analog zur Kante BD im letzten Schritt werden jetzt die Kanten BC, DE und FE rot markiert. |
 |
Als letzte wird die Kante EG mit Länge 9 ausgewählt, da alle kürzeren bzw. gleich langen Kanten entweder schon ausgewählt sind oder einen Kreis bilden würden. Die Kante FG wird rot markiert. Da nun alle nicht ausgewählten Kanten einen Kreis bilden würden (sie sind rot markiert) ist der Algorithmus am Ende angelangt und der grüne Graph ist ein minimaler Spannbaum des zugrundeliegenden Graphen. |
Algorithmus
Die Grundidee ist, die Kanten in Reihenfolge aufsteigender Kantengewichte zu durchlaufen und jede Kante zur Lösung hinzuzufügen, die mit allen zuvor gewählten Kanten keinen Kreis bildet. Es werden somit sukzessiv sogenannte Komponenten zum minimalen Spannbaum verbunden.
Input
Als Eingabe dient ein zusammenhängender kantenbewerteter Graph . bezeichnet die Menge der Knoten (vertices), die Menge der Kanten (edges). Die Gewichtsfunktion ordnet jeder Kante ein Kantengewicht zu.
Output
Der Algorithmus liefert einen minimalen Spannbaum mit .
Pseudocode
Der Algorithmus von Kruskal arbeitet nicht-deterministisch, d. h., er liefert unter Umständen beim wiederholten Ausführen unterschiedliche Ergebnisse. Alle diese Ergebnisse sind minimale Spannbäume von .

G = (V,E,w): ein zusammenhängender, ungerichteter, kantengewichteter Graph kruskal(G) 1 2 3 Sortiere die Kanten in L aufsteigend nach ihrem Kantengewicht. 4 solange 5 wähle eine Kante mit kleinstem Kantengewicht 6 entferne die Kante aus 7 wenn der Graph keinen Kreis enthält 8 dann 9 M = (V,E') ist ein minimaler Spannbaum von G.
Derselbe Algorithmus lässt sich analog für einen maximalen Spannbaum anwenden. Sei etwa ein zusammenhängender kantengewichteter Graph. Dann gibt man mit , und im Algorithmus von Kruskal ein. Als Ausgabe erhält man schließlich einen minimalen Spannbaum von und somit einen maximalen von .
Zum Testen, ob Knoten und in unterschiedlichen Teilbäumen sind, kann eine Union-Find-Struktur verwendet werden. Dann ergibt sich eine Laufzeit von . Dabei ist die Zeit, die zum Sortieren der Kantengewichte benötigt wird und das Inverse der Ackermannfunktion. Für realistische Eingaben ist immer kleiner oder gleich
Programmierung
Das folgende Beispiel in der Programmiersprache C++ zeigt die Implementierung eines ungerichteten Graphen mit einem Array von Kanten. Der ungerichtete Graph wird als Klasse UndirectedGraph deklariert. Bei der Ausführung des Programms wird die Methode main verwendet, die die Kanten und Kantengewichte eines minimalen Spannbaums auf der Konsole ausgibt. Die Funktion unionSubsets verwendet union by rank, um zwei Teilmengen von Kanten des Graphen zu vereinigen.[2]
#include <iostream>
#include <sstream>
using namespace std;
// Deklariert den Datentyp für die Knoten des Graphen
struct Node
{
int index;
string value;
Node* next;
};
// Deklariert den Datentyp für die Kanten des Graphen
struct Edge
{
int startIndex;
int endIndex;
int weight;
};
// Deklariert die Klasse für den ungerichteten Graphen
class UndirectedGraph
{
public:
int numberOfVertices;
Edge* edges; // Pointer auf das Array für die Kanten
};
// Deklariert die Klasse für Teilmengen (Teilbäume) der Kantenmenge des ungerichteten Graphen
class subset
{
public:
int parent; // Index der Wurzel
int rank; // Rang der Teilmenge
};
// Diese rekursive Funktion gibt den Index der Wurzel der Teilmenge (Teilbaum) mit dem Index i zurück
int find(subset subsets[], int i)
{
// Setzt Index der Wurzel auf den Index der Wurzel der Teilmenge mit dem Index i
if (subsets[i].parent != i)
{
subsets[i].parent = find(subsets, subsets[i].parent); // Rekursiver Aufruf der Funktion
}
return subsets[i].parent;
}
// Diese Methode bildet die Vereinigungsmenge der zwei Teilmengen (Teilbäume) mit den Indexen index1 und index2
void unionSubsets(subset subsets[], int index1, int index2)
{
int newIndex1 = find(subsets, index1); // Index der Teilmenge mit dem Index index1
int newIndex2 = find(subsets, index2); // Index der Teilmenge mit dem Index index2
// Hängt den Teilbaum mit dem niedrigeren Rang unter die Wurzel des Baums mit dem höheren Rang
if (subsets[newIndex1].rank < subsets[newIndex2].rank)
{
subsets[newIndex1].parent = newIndex2;
}
else if (subsets[newIndex1].rank > subsets[newIndex2].rank)
{
subsets[newIndex2].parent = newIndex1;
}
else // Wenn die Teilbäume denselben Rang haben, wird der Rang des einen Baums erhöht und der andere Baum unter die Wurzel des anderen Baums gehängt
{
subsets[newIndex2].parent = newIndex1;
subsets[newIndex1].rank++;
}
}
// Diese Funktion vergleicht die Gewichte der Kanten edge1 und edge2
int compare(const void* edge1, const void* edge2)
{
return ((Edge*)edge1)->weight > ((Edge*)edge2)->weight; // Gibt 1 zurück, wenn der Vergleich true ergibt. Gibt 0 zurück, wenn der Vergleich false ergibt.
}
// Diese Funktion verwendet den Algorithmus von Kruskal und gibt den minimalen Spannbaum zurück
Edge* getMSTByKruskal(UndirectedGraph* graph)
{
Edge* edges = graph->edges; // Pointer auf das Array für die Kanten
int numberOfVertices = graph->numberOfVertices; // Variable für die Anzahl der Knoten
int numberOfEdges = sizeof(edges); // Variable für die Anzahl der Kanten
Edge* minimalSpanningTree = new Edge[numberOfVertices]; // Deklariert ein Array für die Kanten, das als Ergebnis der Methode zurückgegeben wird
int currentIndex = 0; // Aktueller Kantenindex
int nextIndex = 0; // Kantenindex für die nächste Iteration
qsort(edges, numberOfEdges, sizeof(edges[0]), compare); // Sortiert das Array edges der Kanten mit der C++-Standardfunktion qsort (Sortierverfahren Quicksort) und der oben definierten Vergleichsfunktion compare
subset* subsets = new subset[numberOfVertices]; // Deklariert ein Array für die Teilmengen der Kantenmenge
for (int i = 0; i < numberOfVertices; i++) // for-Schleife, die Teilmengen mit einzelnen Kanten erzeugt
{
subsets[i].parent = i;
subsets[i].rank = 0;
}
while (currentIndex < numberOfVertices - 1 && nextIndex < numberOfEdges) // So lange der aktuelle Kantenindex kleiner als die Anzahl der Knoten minus 1 ist
{
Edge nextEdge = edges[nextIndex++]; // Weist die verbleibende Kante mit dem kleinsten Kantengewicht zu und erhöht den Kantenindex für die nächste Iteration um 1
int index1 = find(subsets, nextEdge.startIndex); // Index der Wurzel der Teilmenge mit dem Index nextEdge.startIndex
int index2 = find(subsets, nextEdge.endIndex); // Index der Wurzel der Teilmenge mit dem Index nextEdge.endIndex
if (index1 != index2) // Wenn die Kante keinen Zyklus erzeugt
{
minimalSpanningTree[currentIndex++] = nextEdge; // Fügt die Kante dem minimalen Spannbaum hinzu
unionSubsets(subsets, index1, index2); // Methodenaufruf, der die Vereinigungsmenge der zwei Mengen mit den Indexen index1 und index2 bildet
}
}
return minimalSpanningTree;
}
// Gibt die Kanten, die Gewichte und das gesamte Kantengewicht des minimalen Spannbaums auf der Konsole aus
string MSTtoString(Edge* minimalSpanningTree)
{
stringstream text;
int weight = 0;
for (int i = 0; i < sizeof(minimalSpanningTree) - 1; i++)
{
Edge edge = minimalSpanningTree[i];
text << "(" << edge.startIndex << ", " << edge.endIndex << "), Gewicht: " << edge.weight << endl;
weight += edge.weight;
}
text << "Kantengewicht des minimalen Spannbaums: " << weight << endl;
return text.str(); // Typumwandlung von stringstream nach string
}
// Hauptfunktion die das Programm ausführt
int main()
{
// Deklariert und initialisiert ein Array mit 5 Kanten
Edge* edges = new Edge[5];
edges[0].startIndex = 0;
edges[0].endIndex = 1;
edges[0].weight = 10;
edges[1].startIndex = 0;
edges[1].endIndex = 2;
edges[1].weight = 6;
edges[2].startIndex = 0;
edges[2].endIndex = 3;
edges[2].weight = 5;
edges[3].startIndex = 1;
edges[3].endIndex = 3;
edges[3].weight = 15;
edges[4].startIndex = 2;
edges[4].endIndex = 3;
edges[4].weight = 4;
// Erzeugt den ungerichteten Graphen mit den gegebenen Kanten
UndirectedGraph* undirectedGraph = new UndirectedGraph;
undirectedGraph->edges = edges;
undirectedGraph->numberOfVertices = 4;
Edge* minimalSpanningTree = getMSTByKruskal(undirectedGraph); // Aufruf der Methode, die einen Pointer auf das Array von Kanten zurückgibt
cout << MSTtoString(minimalSpanningTree); // Aufruf der Methode, die das Ergebnis auf der Konsole ausgibt
}
Paralleles Sortieren
Das Sortieren der ersten Phase kann parallelisiert werden. In der zweiten Phase ist es für die Korrektheit jedoch wichtig, dass die Kanten nacheinander abgearbeitet werden. Mit Prozessoren kann in linearer Zeit parallel sortiert werden. Dadurch sinkt die Gesamtlaufzeit auf .
Filter-Kruskal
Eine Variante des Algorithmus von Kruskal namens Filter-Kruskal wurde von Osipov et al.[3] beschrieben und eignet sich besser zur Parallelisierung. Die grundlegende Idee besteht darin, die Kanten in ähnlicher Weise wie bei Quicksort zu partitionieren und anschließend Kanten auszusortieren, welche Knoten im gleichen Teilbaum verbinden, um somit die Kosten für die weitere Sortierung zu verringern. Filter-Kruskal eignet sich besser zur Parallelisierung, da das Sortieren, Partitionieren und Filtern einfach parallel ausgeführt werden können, indem die Kanten zwischen den Prozessoren aufgeteilt werden. Der Algorithmus wird im folgenden Pseudocode dargestellt.
filterKruskal(): falls KruskalSchwellwert: return kruskal() pivot = zufällige Kante aus , partition(, pivot) filterKruskal() filter() filterKruskal() return
partition(, pivot): für alle : falls gewicht() gewicht(pivot): sonst return (, )
filter(): für alle : falls find-set(u) find-set(v): return
Korrektheitsbeweis
Sei ein zusammenhängender kantengewichteter Graph und die Ausgabe des Algorithmus von Kruskal. Um nun die Korrektheit des Algorithmus zu beweisen, muss Folgendes gezeigt werden:
- der Algorithmus terminiert (er enthält keine Endlosschleife).
- ist ein minimaler Spannbaum von , also:
- ist spannender Teilgraph von .
- enthält keinen Kreis.
- ist zusammenhängend.
- ist bezüglich minimal.
Im Nachstehenden folgen einige Beweisideen, die die Gültigkeit der einzelnen Aussagen darlegen:
- Terminierung
- Durch Zeile 6 wird in jedem Schleifendurchlauf genau ein Element aus entfernt. Außerdem wird durch keine weitere Operation verändert. Aus werden wegen Zeile 4 nur solange Elemente entfernt, bis . Da zu Beginn im Algorithmus gesetzt wurde und nach Definition nur endlich ist, wird auch die Schleife nur endlich oft durchlaufen. Daraus folgt, dass Kruskals Algorithmus terminiert.
- M ist aufspannender Teilgraph von G
- Da die Menge der Knoten nach Definition des Algorithmus bei und gleich ist und wegen Zeile 8 offensichtlich gilt, ist aufspannender Teilgraph von .
- M enthält keinen Kreis
- Dass keinen Kreis beinhalten kann, ist durch Zeile 7 trivial.
- M ist zusammenhängend
- Im Folgenden wird indirekt gezeigt, dass zusammenhängend ist. Sei also nicht zusammenhängend. Dann gibt es in zwei Knoten und , die nicht durch einen Weg verbunden sind. Da aber und in durch einen Weg verbunden sind, existiert eine Kante in , welche nicht in vorhanden ist. Der Algorithmus betrachtet in Zeile 7 garantiert jede Kante aus und damit auch . Der Graph in Zeile 7 muss kreisfrei sein, da es zwischen und in keinen Weg gibt. Mit Zeile 8 wird dann in eingefügt. Dies widerspricht allerdings der Tatsache, dass nicht in enthalten ist. Somit ist unsere Annahme hinfällig und doch zusammenhängend.
- M ist bezüglich G minimal
- Wir zeigen durch Induktion, dass für die folgende Behauptung wahr ist:
Wenn die Kantenmenge ist, die im -ten Schritt des Algorithmus erzeugt wurde, dann gibt es einen minimalen Spannbaum, der enthält. Die Behauptung ist für wahr, d. h. (d. h., es ist noch keine Kante eingeplant). Jeder minimale Spannbaum erfüllt die Behauptung und es existiert ein minimaler Spannbaum, da ein gewichteter, zusammenhängender Graph immer einen minimalen Spannbaum besitzt. Jetzt nehmen wir an, dass die Behauptung für erfüllt ist und die vom Algorithmus nach Schritt erzeugte Kantenmenge ist. Es sei ein minimaler Spannbaum, der enthält. Wir betrachten jetzt den Fall . Dafür sei die letzte vom Algorithmus eingefügte Kante.
- Falls
- Dann ist die Behauptung auch für erfüllt, da der minimale Spannbaum um eine Kante aus dem minimalen Spannbaum erweitert wird.
- Falls
- Dann enthält einen Kreis und es gibt eine Kante , die im Kreis, aber nicht in liegt. (Wenn es keine solche Kante geben würde, dann hätte nicht zu hinzufügt werden können, da dann ein Kreis entstanden wäre.) Damit ist ein Baum. Weiterhin kann das Gewicht von nicht geringer als das Gewicht von sein, da sonst der Algorithmus anstelle von hinzugefügt hätte. Mit folgt, dass gilt. Da aber minimaler Spannbaum ist, gilt außerdem und daraus folgt . Somit ist ein minimaler Spannbaum, der enthält, und die Behauptung ist erfüllt.
Damit folgt für , dass der Kruskal-Algorithmus nach Schritten eine Menge erzeugt, die zu einem minimalen Spannbaum erweitert werden kann. Da aber das Ergebnis nach Schritten des Algorithmus bereits ein Baum ist (wie oben gezeigt wurde), muss dieser minimal sein.
Zeitkomplexität
Im Folgenden sei die Anzahl der Kanten und die Anzahl der Knoten. Die Laufzeit des Algorithmus setzt sich zusammen aus dem notwendigen Sortieren der Kanten nach ihrem Gewicht und dem Überprüfen, ob der Graph kreisfrei ist. Das Sortieren benötigt eine Laufzeit von . Bei einer geeigneten Implementierung ist das Überprüfen auf Kreisfreiheit schneller möglich, so dass das Sortieren die Gesamtlaufzeit bestimmt. Insbesondere bei Graphen mit vielen Kanten ist insofern der Algorithmus von Prim effizienter.
Wenn die Kanten bereits vorsortiert sind, arbeitet der Algorithmus von Kruskal schneller. Man betrachtet nun, wie schnell das Überprüfen auf Kreisfreiheit möglich ist. Um eine bestmögliche Laufzeit zu erreichen, speichert man alle Knoten in einer Union-Find-Struktur. Diese enthält Informationen darüber, welche Knoten zusammenhängen. Zu Beginn ist noch keine Kante in den Spannbaum eingetragen, daher ist jeder Knoten für sich in einer einzelnen Partition. Wenn eine Kante hinzugefügt werden soll, wird überprüft, ob und in verschiedenen Partitionen liegen. Dazu dient die Operation Find(x): Sie liefert einen Repräsentanten der Partition, in dem der Knoten x liegt. Wenn Find() und Find() verschiedene Ergebnisse liefern, dann kann die Kante hinzugefügt werden und die Partitionen der beiden Knoten werden vereinigt (Union). Ansonsten würde durch Hinzunehmen der Kante ein Kreis entstehen, die Kante wird also verworfen. Insgesamt wird die Operation Find (für jede Kante) und die Operation Union mal aufgerufen. Bei Verwenden der Heuristiken Union-By-Size und Pfadkompression ergibt eine amortisierte Laufzeitanalyse für den Algorithmus eine Komplexität von . Dabei ist definiert als
und praktisch konstant. Theoretisch wächst diese Funktion jedoch unendlich, weshalb sie in der O-Notation nicht weggelassen werden kann.
Parallele Implementierung
Aufgrund von Datenabhängigkeiten zwischen den Iterationen lässt sich der Algorithmus von Kruskal grundsätzlich schwer parallelisieren. Es ist jedoch möglich, das Sortieren der Kanten zu Beginn parallel auszuführen oder alternativ eine parallele Implementation eines Binären Heaps zu verwenden um in jeder Iteration die Kante mit dem kleinsten Gewicht zu finden[4]. Durch paralleles Sortieren, was auf Prozessoren in Zeit möglich ist[5], kann die Laufzeit des Algorithmus auch bei zuvor unsortierten Kanten auf reduziert werden.
Eine Variante des Algorithmus von Kruskal namens Filter-Kruskal wurde von Osipov et al.[3] beschrieben und eignet sich besser zur Parallelisierung. Die grundlegende Idee besteht darin, die Kanten in ähnlicher Weise wie bei Quicksort zu partitionieren und anschließend Kanten auszusortieren, welche Knoten im gleichen Teilbaum verbinden, um somit die Kosten für die Sortierung zu verringern. Der Algorithmus wird im folgenden Pseudocode dargestellt.
FILTER-KRUSKAL(G): 1 if |G.E| < KruskalThreshhold: 2 return KRUSKAL(G) 3 pivot = CHOOSE-RANDOM(G.E) 4 , = PARTITION(G.E, pivot) 5 A = FILTER-KRUSKAL() 6 = FILTER() 7 A = A ∪ FILTER-KRUSKAL() 8 return A
PARTITION(E, pivot): 1 = ∅, = ∅ 2 foreach (u, v) in E: 3 if weight(u, v) <= pivot: 4 = ∪ {(u, v)} 5 else 6 = ∪ {(u, v)} 5 return ,
FILTER(E): 1 = ∅ 2 foreach (u, v) in E: 3 if FIND-SET(u) ≠ FIND-SET(v): 4 = ∪ {(u, v)} 5 return
Filter-Kruskal eignet sich besser zur Parallelisierung, da sowohl das Sortieren und Partitionieren, als auch das Filtern einfach parallel ausgeführt werden kann, indem die Kanten zwischen den Prozessoren aufgeteilt werden.[3]
Weitere Varianten für eine Parallelisierung von Kruskals Algorithmus sind ebenfalls möglich. So besteht zum Beispiel die Möglichkeit, den sequentiellen Algorithmus auf mehreren Teilgraphen parallel auszuführen, um diese dann zusammenzuführen bis schlussendlich nur noch der finale minimale Spannbaum übrigbleibt[6]. Eine simplere Form des Filter-Kruskals, bei welchem Hilfsthreads benutzt werden, um Kanten, die eindeutig nicht Teil des minimalen Spannbaums sind, im Hintergrund zu entfernen, kann ebenfalls verwendet werden[7].
Sonstiges
Der Algorithmus diente Kruskal ursprünglich als Hilfsmittel für einen vereinfachten Beweis, dass ein Graph mit paarweise verschiedenen Kantengewichten einen eindeutigen minimalen Spannbaum besitzt.
Weblinks
Einzelnachweise
- Joseph Kruskal: On the shortest spanning subtree and the traveling salesman problem. In: Proceedings of the American Mathematical Society, 7, 1956, S. 48–50
- GeeksforGeeks: Kruskal’s Minimum Spanning Tree Algorithm
- Vitaly Osipov, Peter Sanders, Johannes Singler: The filter-kruskal minimum spanning tree algorithm. In: Proceedings of the Eleventh Workshop on Algorithm Engineering and Experiments (ALENEX). Society for Industrial and Applied Mathematics. 2009, S. 52–61.
- Michael J. Quinn, Narsingh Deo: Parallel graph algorithms. In: ACM Computing Surveys (CSUR) 16.3. 1984, S. 319–348.
- Ananth Grama, Anshul Gupta, George Karypis, Vipin Kumar: Introduction to Parallel Computing. 2003, ISBN 978-0-201-64865-2, S. 412–413.
- Vladimir Lončar, Srdjan Škrbić, Antun Balaž: Parallelization of Minimum Spanning Tree Algorithms Using Distributed Memory Architectures. In: Transactions on Engineering Technologies. 2014, S. 543–554.
- Anastasios Katsigiannis, Nikos Anastopoulos, Nikas Konstantinos, Nectarios Koziris: An approach to parallelize kruskal’s algorithm using helper threads. In: Parallel and Distributed Processing Symposium Workshops & PhD Forum (IPDPSW), 2012 IEEE 26th International. 2012, S. 1601–1610.