সমকোণ

জ্যামিতি এবং ত্রিকোণমিতিতে, সমকোণ বলতে ৯০° বা /২ রেডিয়ান মাপবিশিষ্ট কোণকে বোঝায়। [1] যদি একটি রশ্মির পাদবিন্দু একটি সরলরেখার উপর অবস্থান করে, এবং সন্নিহিত কোণ দুইটি সমান হয়, তবে তারা সমকোণ।[2]

সমকোণ ৯০ ডিগ্রির সমান
একটি রেখাংশ AB আঁকা হয়েছে যাতে CD রেখার সাথে সমকোণ উৎপন্ন করে।

এর সাথে সম্পর্কযুক্ত এবং গুরুত্বপূর্ণ বিষয় হলো লম্ব রেখা, মানে রেখাগুলি যা তাদের ছেদ বিন্দুতে সমকোণ গঠন করে এবং অর্থোগোনালিটি, যা সমকোণ গঠনের বৈশিষ্ট্য, সাধারণত ভেক্টর রাশিতে প্রয়োগ করা হয়। একটি ত্রিভুজে একটি সমকোণের উপস্থিতি হল সমকোণী ত্রিভুজগুলির জন্য সংজ্ঞায়িত ফ্যাক্টর, [3] ত্রিকোণমিতির জন্য সমকোণ ভিত্তিস্বরূপ।

ব্যুৎপত্তি

সমকোণে সম শব্দটি সম্ভবত ল্যাটিন বিশেষণ রেক্টাস থেকে এসেছে। যার অর্থ 'খাড়া, সোজা, খাড়া, লম্ব' বোঝায়। এটির গ্রীক সমতুল্য শব্দ অর্থোস যার অর্থ 'সোজা অথবা লম্ব'।

প্রাথমিক জ্যামিতিতে

একটি আয়তক্ষেত্র হল চারটি সমকোণ বিশিষ্ট একটি চতুর্ভুজ। একটি বর্গক্ষেত্রে সমান দৈর্ঘ্যের বাহু ছাড়াও চারটি সমকোণ রয়েছে।[4]

পিথাগোরাসের উপপাদ্যটির মাধ্যমে কোন ত্রিভুজ একটি সমকোণী ত্রিভুজ হবে তা নির্ধারণ করা যায়।

প্রতীক
সমকোণ ত্রিভুজ, একটি ছোট বর্গক্ষেত্রের মাধ্যমে দেখানো সমকোণ সহ।
একটি কোণ বক্ররেখা এবং একটি ছোট বিন্দু ব্যবহার করে চিত্রগতভাবে একটি সমকোণ নির্দেশ করার আরেকটি বিকল্প পদ্ধতি।

ইউনিকোডে, সমকোণের প্রতীক হলো U+221F ∟ সমকোণ (এইচটিএমএল: ∟)। অনুরূপ আকৃতির চিহ্নের সাথে বিভ্রান্ত হওয়া উচিত নয়: U+231E ⌞ নীচের বাম কোণে (এইচটিএমএল: ⌞). সম্পর্কিত প্রতীকগুলো হলো U+22BE ⊾ চাপসহ সমকোণ (এইচটিএমএল: ⊾), U+299C ⦜ বর্গসহ ভিন্ন সমকোণ (এইচটিএমএল: ⦜), এবং U+299D ⦝ বিন্দুসহ সমকোণ (এইচটিএমএল: ⦝)।[5]

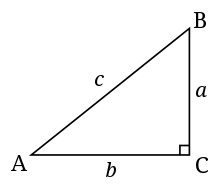
ডায়াগ্রামে, একটি কোণ আছে যা একটি সমকোণ। এটির সাথে একটি ছোট সমকোণ যোগ করে প্রকাশ করা হয় যা ডায়াগ্রামের কোণের সাথে একটি বর্গক্ষেত্র তৈরি করে, যেমনটি ডানদিকের সমকোণী ত্রিভুজের চিত্রে দেখা যাচ্ছে (ব্রিটিশ ইংরেজিতে, একটি সমকোণ ত্রিভুজ)। এটি মাপা কোণের প্রতীক, একটি বিন্দু সহ একটি চাপ, জার্মান-ভাষী দেশ এবং পোল্যান্ড সহ কিছু ইউরোপীয় দেশে সমকোণের এই বিকল্প প্রতীক হিসাবে ব্যবহৃত হয়।[6]

ইউক্লিড

সমকোণ ইউক্লিড এর এলিমেন্টস গ্রন্থের মৌলিক বিষয়। ১ নং বইয়ের ১০ নং সংজ্ঞায় সমকোনের সংজ্ঞা দেওয়া হয়েছে। যেখানে সমান্তরাল রেখারও সংজ্ঞা দেওয়া হয়েছে। ১০ নং সংজ্ঞায় কোন পরিমাপের একক ব্যবহার করা হয় নি। বরং সমকোণের প্রকৃত সংজ্ঞা দেওয়া হয়েছে। দুইটি সরলরেখা একে অপরকে ছেদ করলে সন্নিহিত কোণ দুইটি পরস্পর সমান হলে, তারা উভয়েই সমকোণ।[7] যে সরলরেখাগুলো সমকোণ গঠন করে সেই দুটি রেখাকে পরস্পরের লম্ব বলে।[8] ১১ এবং ১২ নং সংজ্ঞায় সূক্ষ্মকোণ(সমকোণ হতে ছোট) এবং স্থুলকোণকে(সমকোণ হতে বড়) সংজ্ঞায়িত করতে ইউক্লিড সমকোণ ব্যবহার করেছেন। দুইটি কোণের সমষ্টি এক সমকোণ হলে, তারা পরস্পর পূরক কোণ।[9]

১ নং বইয়ের ৪ নং প্রতিজ্ঞায় বলা হয়েছে, প্রতিটি সমকোণ সমান। যার ফলে ইউক্লিড সমকোণকে কোণ মাপার একক হিসেবে ব্যবহার করেছেন। ইউক্লিডের সমালোচক প্রোক্লাস পূর্ববর্তী প্রতিজ্ঞাগুলি ব্যবহার করে এই অনুমানটির একটি প্রমাণ দিয়েছেন, তবে এটি যুক্তি দেওয়া যেতে পারে যে এই প্রমাণটি কিছু গোপন অনুমান ব্যবহার করে করা হয়েছিল। সাচেরি একটি প্রমাণও দিয়েছেন তবে আরও স্পষ্ট ধারণা ব্যবহার করেছেন। হিলবার্টের জ্যামিতির স্বতঃসিদ্ধকরণে এই বিবৃতিটি একটি উপপাদ্য হিসাবে দেওয়া হয়েছে, তবে শুধুমাত্র অনেক ভিত্তির পরে। কেউ যুক্তি দিতে পারে যে, এমনকি যদি পূর্ববর্তীগুলি থেকে ৪ নং প্রতিজ্ঞা প্রমাণ করা যায়, ইউক্লিড যে ক্রমে তার উপাদানটি উপস্থাপন করেছেন তাতে এটি অন্তর্ভুক্ত করা আবশ্যক কারণ এটি ৫ নং প্রতিজ্ঞা ব্যতীত, যা পরিমাপের একক হিসাবে সমকোণ ব্যবহার করে।[10]

অন্যান্য এককে রূপান্তর

সমকোণকে বিভিন্ন এককে প্রকাশ করা যায়:

  • ১/৪ বৃত্ত
  • ৯০° (ডিগ্রি)
  • /২ রেডিয়ান
  • ১০০ গ্রেডিয়ান
  • ৬ ঘন্টা (জ্যোতির্বৈজ্ঞানিক ঘন্টা কোণ)

৩-৪-৫ নিয়ম

ইতিহাস হতে, ছুতার এবং রাজমিস্ত্রিরা একটি ত্রিভুজ সমকোণী কি না তা জানার উপায় জানতেন। বহুল ব্যবহৃত পিথাগোরাস ত্রয়ী (৩,৪,৫) এর উপর ভিত্তি করেই এটি রচিত এবং এটিকে ৩-৪-৫ নিয়ম বলা হয়। যে কোনটিকে মাপা হবে, সে কোণটির এক দিকে ৩ একক এবং অপর দিকে ৪ একক লাইন টানতে হবে এবং অতিভুজটি যদি ৫ একক হয় তবে এটি একটি সমকোণ। এই নিয়মের জ্যামিতিক ব্যাখ্যা হলো পিথাগোরাসের উপপাদ্য।

থেলসের উপপাদ্য
P বিন্দু থেকে অর্ধ-রেখা h এর লম্ব নির্মাণ (শুধুমাত্র শেষ বিন্দু A এ প্রযোজ্য নয়, M অবাধে নির্বাচনযোগ্য), অ্যানিমেশন শেষে ১০ সেকেন্ড বিরতি দিয়ে
বিকল্প নির্মাণ যদি P অর্ধ-রেখা h এর বাইরে এবং দূরত্ব A থেকে P' ছোট হয় (B অবাধে নির্বাচনযোগ্য), অ্যানিমেশন শেষে ১০ সেকেন্ড বিরতি দিয়ে
মূল নিবন্ধ: থেলসের উপপাদ্য

থেলসের উপপাদ্য অনুসারে অর্ধবৃত্তে অন্তর্লিখিত কোণ সমকোণ।

অন্যভাবে বলতে গেলে অর্ধবৃত্তস্থ কোণ এক সমকোণ।

আরও দেখুন
উইকিমিডিয়া কমন্সে সমকোণ সংক্রান্ত মিডিয়া রয়েছে।

তথ্যসূত্র
  1. "Right Angle"। Math Open Reference। সংগ্রহের তারিখ ২৬ এপ্রিল ২০১৭।
  2. "Wentworth, Sir Thomas, Baron Wentworth (1613–1665)"। Oxford Dictionary of National Biography। Oxford University Press। ২০১৮-০২-০৬।
  3. "Wentworth, Henrietta Maria, Baroness Wentworth (1657?–1686)"। Oxford Dictionary of National Biography। Oxford University Press। ২০১৮-০২-০৬।
  4. "বর্গ কাকে বলে"। Edudesh। ২০১৫-০৬-১৪। সংগ্রহের তারিখ ২০২১-১২-০৬।
  5. Crispin, M. (2007-10)। "i;unicode-casemap - Simple Unicode Collation Algorithm"। এখানে তারিখের মান পরীক্ষা করুন: |তারিখ= (সাহায্য)
  6. Müller-Philipp, Susanne; Gorski, Hans-Joachim (২০১১)। Leitfaden Geometrie (জার্মান ভাষায়)। Springer। আইএসবিএন ৯৭৮৩৮৩৪৮৮৬১৬৩ |আইএসবিএন= এর মান পরীক্ষা করুন: invalid character (সাহায্য)।
  7. Heath, Harold (১৯১১)। The Solenogastres / by Harold Heath। Cambridge, U.S.A: Printed for the Museum।
  8. Heath, Harold (১৯১১)। The Solenogastres / by Harold Heath। Cambridge, U.S.A: Printed for the Museum।
  9. "Wentworth, Henrietta Maria, Baroness Wentworth (1657?–1686)"। Oxford Dictionary of National Biography। Oxford University Press। ২০১৮-০২-০৬।
  10. Heath, Harold (১৯১১)। The Solenogastres / by Harold Heath। Cambridge, U.S.A: Printed for the Museum।
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.