জাদু বর্গ

n পর্যায়ের জাদু বর্গ হল, একটি বর্গাকারে সাজানো n² সংখ্যক পূর্ণ সংখ্যার,(সাধারনতঃ ভিন্ন ভিন্ন) সমাবেশ যেন, প্রত্যেক সারি,স্তম্ভ এবং কর্ণ বরাবর সংখ্যাগুলির যোগফল একই হয়। একটি সাধারণ জাদু বর্গে 1 থেকে n² পর্যন্ত পূর্ণ সংখ্যাগুলি থাকে।

n≥ 1 পর্যায় বিশিষ্ট সকল সাধারণ জাদুবর্গের অস্তিত্ব রয়েছে, তবে 2 পর্যায়ের জাদুবর্গের অস্তিত্ব নেই। 1 পর্যায়ের জাদু বর্গ নগণ্য(ইংরেজি trivial)-এর একটি মাত্র ঘর রয়েছে। ক্ষুদ্রতম অনগণ্য জাদু বর্গ নিচে দেখানো হল। এর পর্যায় 3।

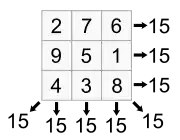
প্রত্যেক সারি, স্তম্ভ এবং কর্ণ বরাবর ধ্রুবক সমষ্টিকে জাদু ধ্রুবক(ইংরেজি magic constant),M বলা হয়। সাধারণ জাদু বর্গের জাদু ধ্রুবকের মান শুধুমাত্র nএর উপর নির্ভর করে।

M(n)={\frac {n^{3}+n}{2}}

মধ্যম সংখ্যাটি নিম্নরূপ,

{\frac {n^{2}+1}{2}}

n = 3, 4, 5, …, পর্যায়ের জাদু বর্গের জন্য জাদু ধ্রুবকের মান যথাক্রমে,

15, 34, 65, 111, 175, 260, …

এর ধরন

জাদু বর্গ বিভিন্ন রকম হতে পারে।এর মধ্যে প্রধান ভাগ গুলো হলঃ

1.(2n-1)*(2n-1)

2.4n*4n

3.(4n+2)*(4n+2)

1.(2n-1)*(2n-1)

জাদু বর্গ এর সবচে সহজ ধরন হল (2n-1)*(2n-1) জাদুবর্গ।এ ক্ষেত্রে প্রথমে বর্গটির যে কোন সারির মধ্যের ঘরে ১ লিখতে হবে।এর পর উপরে এক ঘর এবং ডানে এক ঘর গিয়ে ২ লিখতে হবে।যে ঘরে নাম্বার বসবে সেই ঘরে আগে থেকেই যদি অন্য নাম্বার লিখা থাকে তবে সর্বশেষ যে ঘরে নাম্বার লিখা হয়েছে ঠিক তার নিচের ঘরে পরের নাম্বার লিখে আগের মত করে আবার নাম্বার বসানো শুরু করতে হবে।এভাবে লিখতে থাকলে জাদুবর্গ টি সম্পূর্ণ হবে। তবে মনে রাখতে হবে জাদুবর্গ বানানর সময় একে 3D তলে এটি গোলক কল্পনা করতে হবে।অর্থাৎ যদি উপরের সারিতে শেষ নাম্বার টি বসে তবে নিছের ঘরে কলাম্ বরাবর এক ঘর ডানে পরের নাম্বার বসবে।...

	1

	1

		2

	1
3
		2

	1
3
4		2

	1	6
3	5
4		2

	1	6
3	5	7
4		2

8	1	6
3	5	7
4	9	2

তথ্যসূত্র

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.