Цялесны вугал
Вывучаецца ў	стэрэаметрыя
ISQ dimension	${\displaystyle 1}$
Формула, якая апісвае закон або тэарэму	${\displaystyle \Omega =A/r^{2}}$[1]
Пазначэнне ў формуле	${\displaystyle \Omega }$, ${\displaystyle A}$ і ${\displaystyle r}$
Сімвал велічыні (LaTeX)	${\displaystyle \Omega }$
Рэкамендуемая адзінка вымярэння	стэрадыян[2][3][…] і 1[2]
Медыяфайлы на Вікісховішчы

Цялесны вугал

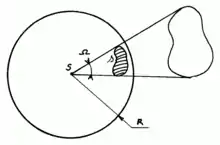
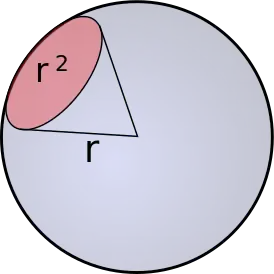
Цялесны вугал — частка прасторы, якая з’яўляецца аб’яднаннем усіх прамянёў, якія выходзяць з дадзенай кропкі (вяршыні вугла) і перасякаюць некаторую паверхню (якая называецца паверхняй, якая сцягвае дадзены цялесны вугал). Асобнымі выпадкамі цялеснага вугла з’яўляюцца трохгранныя і шматгранныя вуглы. Мяжой цялеснага вугла з’яўляецца некаторая канічная паверхня.

Цялесны вугал вымяраецца адносінай плошчы той часткі сферы з цэнтрам у вяршыні вугла, якая выражаецца гэтым цялесным вуглом, да квадрата радыуса сферы:

${\displaystyle \Omega \,=\,{S \over R^{2}}.}$

Відавочна, цялесныя вуглы вымяраюцца адцягненымі (безразмернымі) велічынямі. Адзінкай вымярэння цялеснага вугла ў сістэме СІ з’яўляецца стэрадыян, роўны цялеснаму вуглу, выразаючаму са сферы радыуса ${\displaystyle ~r}$ паверхню з плошчай ${\displaystyle ~r^{2}}$. Поўная сфера ўтварае цялесны вугал, роўны ${\displaystyle ~4\pi }$ стэрадыян (поўны цялесны вугал), для вяршыні, размешчанай унутры сферы, у прыватнасці, для цэнтра сферы; такім жа з’яўляецца цялесны вугал, пад якім бачна любая замкнёная паверхня з кропкі, якая цалкам ахопліваецца гэтай паверхняй, але не належыць ёй. Акрамя стэрадыянаў, цялесны вугал можа вымярацца ў квадратных градусах, квадратных хвілінах і квадратных секундах, а таксама ў долях поўнага цялеснага вугла.

Цялесны вугал мае нулявую фізічную размернасць.

Пазначаецца цялесны вугал звычайна літарай ${\displaystyle ~\Omega }$.

Дваісты цялесны вугал да дадзенага цялеснага вугла ${\displaystyle ~\Omega }$ вызначаецца як вугал, які складаецца з прамянёў, якія ўтвараюць з любым прамянём вугла ${\displaystyle ~\Omega }$ нявостры вугал.

Каэфіцыенты пераліку адзінак цялеснага вугла.

${\displaystyle ~\Omega }$	Стэрадыян	Кв. градус	Кв. хвіліна	Кв. секунда	Поўны вугал
1 стэрадыян =	1	(180/π)² ≈ ≈ 3282,806 кв. градусаў	(180×60/π)² ≈ ≈ 1,1818103×107 кв. хвілін	(180×60×60/π)² ≈ ≈ 4,254517×1010 кв. секунд	1/4π ≈ ≈ 0,07957747 поўнага вугла
1 кв. градус =	(π/180)² ≈ ≈ 3,0461742×10−4 стэрадыян	1	60² = = 3600 кв. хвілін	(60×60)² = = 12 960 000 кв. секунд	π/(2×180)² ≈ ≈ 2,424068×10−5 поўнага вугла
1 кв. хвіліна =	(π/(180×60))² ≈ ≈ 8,461595×10−8 стэрадыян	1/60² ≈ ≈ 2,7777778×10−4 кв. градусаў	1	60² = = 3600 кв. секунд	π/(2×180×60)² ≈ ≈ 6,73352335×10−9 поўнага вугла
1 кв. секунда =	(π/(180×60×60))² ≈ ≈ 2,35044305×10−11 стэрадыян	1/(60×60)² ≈ ≈ 7,71604938×10−8 кв. градусаў	1/60² ≈ ≈ 2,7777778×10−4 кв. хвілін	1	π/(2×180×60×60)² ≈ ≈ 1,87042315×10−12 поўнага вугла
Поўны вугал =	4π ≈ ≈ 12,5663706 стэрадыян	(2×180)²/π ≈ ≈ 41252,96125 кв. градусаў	(2×180×60)²/π ≈ ≈ 1,48511066×108 кв. хвілін	(2×180×60×60)²/π ≈ ≈ 5,34638378×1011 кв. секунд	1

Вылічэнне цялесных вуглоў

Для адвольнай сцягвальнай паверхні ${\displaystyle S}$ цялесны вугал ${\displaystyle \Omega }$, пад якім яна бачная з пачатку каардынат, роўны

${\displaystyle \Omega =\iint \limits _{S}d\Omega =\iint \limits _{S}\sin \vartheta d\varphi d\vartheta =\iint \limits _{S}{\frac {(\mathbf {r} /r)\cdot \mathbf {n} dS}{r^{2}}},}$

дзе ${\displaystyle r,\vartheta ,\varphi }$ — сферычныя каардынаты элемента паверхні ${\displaystyle dS,}$ ${\displaystyle \mathbf {r} }$ — яго радыус-вектар, ${\displaystyle \mathbf {n} }$ — адзінкавы вектар, нармальны да${\displaystyle dS.}$

Уласцівасці цялесных вуглоў

• Поўны цялесны вугал (поўная сфера) роўны ${\displaystyle 4\pi }$ стэрадыян.
• Сума ўсіх цялесных вуглоў, дваістых да ўнутраных цялесных вуглоў выпуклага шматгранніка, роўная поўнаму вуглу.

Велічыні некаторых цялесных вуглоў

• Трохвугольнік з каардынатамі вяршынь ${\displaystyle \mathbf {r} _{1}}$, ${\displaystyle \mathbf {r} _{2}}$, ${\displaystyle \mathbf {r} _{3}}$ бачны з пачатку каардынат пад цялесным вуглом

${\displaystyle \Omega =2\,\mathrm {arctg} \,{\frac {(\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})}{r_{1}r_{2}r_{3}+(\mathbf {r} _{1}\cdot \mathbf {r} _{2})r_{3}+(\mathbf {r} _{2}\cdot \mathbf {r} _{3})r_{1}+(\mathbf {r} _{3}\cdot \mathbf {r} _{1})r_{2}}},}$

дзе ${\displaystyle (\mathbf {r} _{1}\mathbf {r} _{2}\mathbf {r} _{3})}$ — змешаны здабытак дадзеных вектараў, ${\displaystyle (\mathbf {r} _{i}\cdot \mathbf {r} _{j})}$ — скалярны здабытак адпаведных вектараў, паўтлустым шрыфтам пазначаныя вектары, нармальным шрыфтам — іх даўжыні. Па гэтай формуле можна вылічаць цялесныя вуглы, сцягнутыя адвольнымі шматвугольнікамі з вядомымі каардынатамі вяршынь (для гэтага дастаткова разбіць многавугольнік на неперасякальныя трохвугольнікі).

• Цялесны вугал пры вяршыні прамога кругавога конуса з вуглом раствора α роўны ${\displaystyle \Omega =2\pi (1-\cos {\frac {\alpha }{2}})}$. Калі вядомы радыус асновы ${\displaystyle R}$ і вышыня ${\displaystyle H}$ конуса, то ${\displaystyle \Omega =2\pi (1-{\frac {H}{\sqrt {R^{2}+H^{2}}}})}$.

Калі вугал раствора конуса малы,${\displaystyle \Omega \approx {\frac {\pi \alpha ^{2}}{4}}}$ (${\displaystyle \alpha }$ выражана ў радыянах), ці ${\displaystyle \Omega \approx 0,000239\alpha ^{2}}$ (${\displaystyle \alpha }$ выражана ў градусах). Так, цялесны вугал, пад якім з Зямлі бачныя Месяц і Сонца (іх вуглавы дыяметр прыкладна роўны 0,5°), складае каля 6.10⁻⁵ стэрадыян, або ≈ 0,0005 % плошчы нябеснай сферы (гэта значыць поўнага цялеснага вугла).

• Цялесны вугал двухграннага вугла ў стэрадыянах роўны падвоенаму значэнню двухграннага вугла ў радыянах:

• Цялесны вугал трохграннага вугла выражаецца па тэарэме Люілье праз яго плоскія вуглы ${\displaystyle \theta _{a},\theta _{b},\theta _{c}}$ пры вяршыні як:

${\displaystyle \Omega =4\,\operatorname {arctg} {\sqrt {\operatorname {tg} \left({\frac {\theta _{s}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}}}$, где ${\displaystyle \theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}}$ — паўперыметр.

Праз двухгранныя вуглы ${\displaystyle \alpha ,\beta ,\gamma }$ цялесны вугал выражаецца як:

${\displaystyle \Omega =\alpha +\beta +\gamma -\pi }$

• Цялесны вугал пры вяршыні куба (або любога іншага прамавугольнага паралелепіпеда) роўны ${\displaystyle {\frac {1}{8}}}$ поўнага цялеснага вугла, або ${\displaystyle {\frac {\pi }{2}}}$ стэрадыян.

• Цялесны вугал, пад якім бачная грань правільнага N-гранніка з яго цэнтра, роўны ${\displaystyle {\frac {1}{N}}}$ поўнага цялеснага вугла, або ${\displaystyle {\frac {4\pi }{N}}}$ стэрадыян.

Гл. таксама

• Вугал
• Двухгранны вугал
• Трохгранны вугал
• Шматгранны вугал

Зноскі

Спасылкі