Размеркаванне Эрланга

Шчыльнасць імавернасці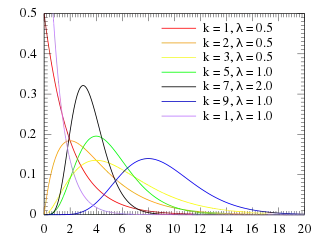
Функцыя размеркавання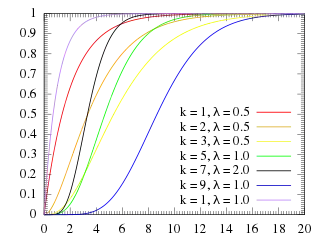
Параметры	${\displaystyle k\in \{1,2,3,\ldots \},}$ форма ${\displaystyle \lambda \in (0,\infty ),}$ частата альтэрнатыўна: ${\displaystyle \beta =1/\lambda ,}$ маштаб
Носьбіт функцыі	${\displaystyle x\in [0,\infty )}$
Шчыльнасць імавернасці	${\displaystyle {\frac {\lambda ^{k}x^{k-1}e^{-\lambda x}}{(k-1)!}}}$
Функцыя размеркавання	${\displaystyle P(k,\lambda x)={\frac {\gamma (k,\lambda x)}{(k-1)!}}=1-\sum _{n=0}^{k-1}{\frac {1}{n!}}e^{-\lambda x}(\lambda x)^{n}}$
Матэматычнае спадзяванне	${\displaystyle {\frac {k}{\lambda }}}$
Медыяна	Няма аналітычнай формы
Мода	${\displaystyle {\frac {1}{\lambda }}(k-1)}$
Дысперсія	${\displaystyle {\frac {k}{\lambda ^{2}}}}$
Каэфіцыент асіметрыі	${\displaystyle {\frac {2}{\sqrt {k}}}}$
Каэфіцыент эксцэсу	${\displaystyle {\frac {6}{k}}}$
Энтрапія	${\displaystyle (1-k)\psi (k)+\ln \left[{\frac {\Gamma (k)}{\lambda }}\right]+k}$
Утваральная функцыя момантаў	${\displaystyle \left(1-{\frac {t}{\lambda }}\right)^{-k}}$ для ${\displaystyle t<\lambda }$
Характарыстычная функцыя	${\displaystyle \left(1-{\frac {it}{\lambda }}\right)^{-k}}$

Размеркаванне Эрланга — абсалютна непарыўнае размеркаванне імавернасцей з ненулявой шчыльнасцю на прамені ${\displaystyle [0,\infty )}$ і двума параметрамі:

• дадатны цэлы лік ${\displaystyle k}$ — каэфіцыент формы;
• дадатны рэчаісны лік ${\displaystyle \lambda }$ — каэфіцыент частаты; часам замест яго ўжываецца ${\displaystyle \beta =1/\lambda }$ — каэфіцыент маштабу.

Размеркаванне Эрланга мае сума ${\displaystyle k}$ незалежных паказнікава размеркаваных выпадковых велічынь з матэматычным спадзяваннем, роўным ${\displaystyle 1/\lambda .}$ Акрамя таго, гэта размеркаванне часу да здарэння ${\displaystyle k}$-й падзеі у працэсе Пуасона з частатой ${\displaystyle \lambda }$.

Калі ${\displaystyle k=1}$, размеркаванне Эрланга становіцца паказнікавым. Размеркаванне Эрланга — асобны выпадак гама-размеркавання з натуральным каэфіцыентам формы^[1]:88.

Размеркаванне Эрланга было распрацавана Агнерам Эрлангам каб падлічыць колькасць званкоў, якую можна напраўляць адначасова аператарам тэлефонных станцый. Гэтая праца па вывучэнні тэлефоннага трафіку была пашырана для мадэлявання часу чакання ў разнастайных сістэмах масавага абслугоўвання. Размеркаванне таксама выкарыстоўваецца ў галіне выпадковых працэсаў.

Азначэнне

Кажуць, што выпадковая велічыня мае размеркаванне Эрланга, калі яе шчыльнасць роўная^[1]:88

${\displaystyle f(x)={\begin{cases}{\frac {\lambda ^{k}}{(k-1)!}}x^{k-1}e^{-\lambda x},&x>0,\\0,&x\leq 0.\end{cases}}}$

Зноскі