Размеркаванне Дзірыхле

Шчыльнасць імавернасці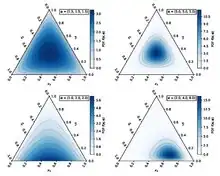
Параметры	${\displaystyle K\geq 2}$ колькасць катэгорый (цэлая) ${\displaystyle {\boldsymbol {\alpha }}=(\alpha _{1},\ldots ,\alpha _{K})}$ параметры канцэнтрацыі, дзе ${\displaystyle \alpha _{i}>0}$
Носьбіт функцыі	${\displaystyle x_{1},\ldots ,x_{K}}$ дзе ${\displaystyle x_{i}\in [0,1]}$ і ${\displaystyle \sum _{i=1}^{K}x_{i}=1}$
Шчыльнасць імавернасці	${\displaystyle {\frac {1}{\mathrm {B} ({\boldsymbol {\alpha }})}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1}}$ дзе ${\displaystyle \mathrm {B} ({\boldsymbol {\alpha }})={\frac {\prod _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma {\bigl (}\alpha _{0}{\bigr )}}}}$ дзе ${\displaystyle \alpha _{0}=\sum _{i=1}^{K}\alpha _{i}}$
Матэматычнае спадзяванне	${\displaystyle \operatorname {E} [X_{i}]={\frac {\alpha _{i}}{\alpha _{0}}}}$ ${\displaystyle \operatorname {E} [\ln X_{i}]=\psi (\alpha _{i})-\psi (\alpha _{0})}$ (дзе ${\displaystyle \psi }$ — дыгама-функцыя)
Мода	${\displaystyle x_{i}={\frac {\alpha _{i}-1}{\alpha _{0}-K}},\quad \alpha _{i}>1.}$
Дысперсія	${\displaystyle \operatorname {Var} [X_{i}]={\frac {{\tilde {\alpha }}_{i}(1-{\tilde {\alpha }}_{i})}{\alpha _{0}+1}},}$ ${\displaystyle \operatorname {Cov} [X_{i},X_{j}]={\frac {\delta _{ij}\,{\tilde {\alpha }}_{i}-{\tilde {\alpha }}_{i}{\tilde {\alpha }}_{j}}{\alpha _{0}+1}}}$ дзе ${\displaystyle {\tilde {\alpha }}_{i}={\frac {\alpha _{i}}{\alpha _{0}}}}$, і ${\displaystyle \delta _{ij}}$ — дэльта Кронекера
Энтрапія	${\displaystyle H(X)=\log \mathrm {B} ({\boldsymbol {\alpha }})}$${\displaystyle +(\alpha _{0}-K)\psi (\alpha _{0})-}$${\displaystyle \sum _{j=1}^{K}(\alpha _{j}-1)\psi (\alpha _{j})}$ дзе ${\displaystyle \alpha _{0}}$ вызначаецца як і для дысперсіі, а ${\displaystyle \psi }$ — дыгама-функцыя
Метад момантаў	${\displaystyle \alpha _{i}=E[X_{i}]\left({\frac {E[X_{j}](1-E[X_{j}])}{V[X_{j}]}}-1\right)}$ дзе ${\displaystyle j}$ некаторы індэкс, у тым ліку можа быць роўны ${\displaystyle i}$

Размеркаванне Дзірыхле — многавымернае абсалютна непарыўнае размеркаванне, параметрам якога ёсць вектар ${\displaystyle {\boldsymbol {\alpha }}}$ дадатных рэчаісных лікаў. Як многавымернае абагульненне бэта-размеркавання^[1], мае альтэрнатыўную назву многавымернае бэта-размеркаванне^[2]. Размеркаванне Дзірыхле часта выкарыстоўваецца як апрыёрнае ў баесаўскай статыстыцы і выступае ў якасці спалучанага апрыёрнага для катэгарыяльнага і паліномнага размеркаванняў.

Названа ў гонар Іагана Петэра Густава Лежона Дзірыхле. Часта абазначаецца як ${\displaystyle \operatorname {Dir} ({\boldsymbol {\alpha }}).}$

Бясконцавымернае абагульненне размеркавання Дзірыхле — працэс Дзірыхле.

Азначэнне

Размеркаваннем Дзірыхле парадку ${\displaystyle K}$ з параметрамі ${\displaystyle \alpha _{1},\alpha _{2},\dots ,\alpha _{K}}$ завецца размеркаванне выпадковага вектара з ${\displaystyle K-1}$ каардынатамі, калі шчыльнасць гэтага размеркавання роўная

${\displaystyle f_{Dir(\alpha _{1},\ldots ,\alpha _{K})}\left(x_{1},\ldots ,x_{K}\right)={\frac {1}{\mathrm {B} ({\boldsymbol {\alpha }})}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1},}$

дзе ${\displaystyle \{x_{k}\}_{k=1}^{k=K}}$ належыць стандартнаму ${\displaystyle K-1}$ сімплексу, то бок ${\displaystyle \sum _{i=1}^{K}x_{i}=1}$ і ${\displaystyle x_{i}\in \left[0,1\right]}$ для ўсіх ${\displaystyle i\in \{1,\dots ,K\}}$

Нарміровачны множнік — многавымерная бэта-функцыя, якую можна запісаць з дапамогай гама-функцый як

${\displaystyle \mathrm {B} ({\boldsymbol {\alpha }})={\frac {\prod \limits _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma \left(\sum \limits _{i=1}^{K}\alpha _{i}\right)}},\qquad {\boldsymbol {\alpha }}=(\alpha _{1},\ldots ,\alpha _{K}).}$

Зноскі