Размеркаванне Бэрнулі

Фунцыя імавернасці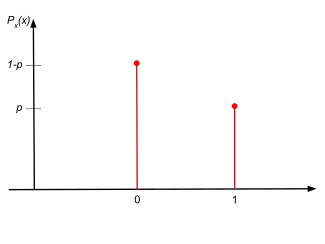
Параметры	${\displaystyle 0\leq p\leq 1,}$ ${\displaystyle q=1-p}$
Носьбіт функцыі	${\displaystyle k\in \{0,1\}}$
Функцыя імавернасці	${\displaystyle {\begin{cases}1-p&k=0\\p&k=1\end{cases}}}$
Функцыя размеркавання	${\displaystyle {\begin{cases}0&k<0\\1-p&0\leq k<1\\1&k\geq 1\end{cases}}}$
Матэматычнае спадзяванне	${\displaystyle p}$
Медыяна	${\displaystyle {\begin{cases}0&p<1/2\\\left[0,1\right]&p=1/2\\1&p>1/2\end{cases}}}$
Мода	${\displaystyle {\begin{cases}0&p<1/2\\0,1&p=1/2\\1&p>1/2\end{cases}}}$
Дысперсія	${\displaystyle p(1-p)=pq}$
Сярэдняе абсалютнае адхіленне	${\displaystyle {\frac {1}{2}}}$
Каэфіцыент асіметрыі	${\displaystyle {\frac {q-p}{\sqrt {pq}}}}$
Каэфіцыент эксцэсу	${\displaystyle {\frac {1-6pq}{pq}}}$
Энтрапія	${\displaystyle -q\ln q-p\ln p}$
Утваральная функцыя момантаў	${\displaystyle q+pe^{t}}$
Характарыстычная функцыя	${\displaystyle q+pe^{it}}$
Імавернасная ўтваральная функцыя	${\displaystyle q+pz}$
Інфармацыя Фішэра	${\displaystyle {\frac {1}{pq}}}$

Размеркаванне Бернулі або Бэрнулі^[1]:81 — дыскрэтнае размеркаванне імавернасцей выпадковай велічыні, якая прымае значэнне 1 з імавернасцю ${\displaystyle p}$ і значэнне 0 з імавернасцю ${\displaystyle q=1-p}$. Прыклад размеркавання Бэрнулі — падкіданне манеты, дзе выпадзенне арла можна супаставіць значэнню 1, а рэшкі — значэнню 0. У выпадку, калі манета «сумленная», імавернасці выпадзення арла і рэшкі мусяць быць роўнымі, а значыць ${\displaystyle p=0.5}$.

Размеркаванне Бэрнулі названае ў гонар швейцарскага матэматыка Якаба Бэрнулі.

Азначэнне

Выпадковая велічыня ${\displaystyle X}$ мае размеркаванне Бэрнулі (запісваецца ${\displaystyle X\sim Bernoulli(p)}$), калі выконваецца

${\displaystyle P(X=1)=p,}$

${\displaystyle P(X=0)=1-p.}$

Для спрашчэння натацыі часта ўводзіцца параметр ${\displaystyle q:=1-p.}$

Функцыя імавернасці мае выгляд

${\displaystyle p_{X\sim Bernoulli(p)}(k)={\begin{cases}p&k=1,\\1-p&k=0.\end{cases}}}$^[2]

Таксама можна запісаць

${\displaystyle p_{X\sim Bernoulli(p)}(k)=p^{k}(1-p)^{1-k}\quad k\in \{0,1\}}$

або

${\displaystyle p_{X\sim Bernoulli(p)}(k)=pk+(1-p)(1-k)\quad k\in \{0,1\}.}$

Характарыстыкі

Матэматычнае спадзяванне выпадковай велічыні, якая мае размеркаванне Бэрнулі, роўнае^[1]:118

${\displaystyle \mathbb {E} [X]=1\cdot p+0\cdot (1-p)=p.}$

Дысперсія роўная^[1]:118

${\displaystyle Var(X)=\mathbb {E} [X^{2}]-\mathbb {E} [X]^{2}=1^{2}\cdot p+0^{2}\cdot (1-p)-p^{2}=p\cdot (1-p)=pq.}$

Сувязь з іншымі размеркаваннямі

Зноскі