Гіпергеаметрычнае размеркаванне

Фунцыя імавернасці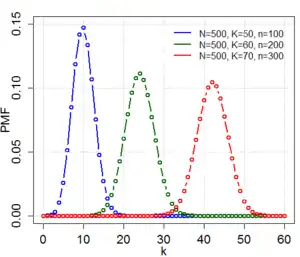
Функцыя размеркавання
Параметры	${\displaystyle {\begin{aligned}N&\in \left\{0,1,2,\dots \right\}\\K&\in \left\{0,1,2,\dots ,N\right\}\\n&\in \left\{0,1,2,\dots ,N\right\}\end{aligned}}\,}$
Носьбіт функцыі	${\displaystyle \scriptstyle {k\,\in \,\left\{\max {(0,\,n+K-N)},\,\dots ,\,\min {(n,\,K)}\right\}}\,}$
Функцыя імавернасці	${\displaystyle {{{K \choose k}{{N-K} \choose {n-k}}} \over {N \choose n}}}$
Функцыя размеркавання	${\displaystyle 1-{{{n \choose {k+1}}{{N-n} \choose {K-k-1}}} \over {N \choose K}}\,_{3}F_{2}\!\!\left[{\begin{array}{c}1,\ k+1-K,\ k+1-n\\k+2,\ N+k+2-K-n\end{array}};1\right],}$ дзе ${\displaystyle \,_{p}F_{q}}$ — абагульненая гіпергеаметрычная функцыя
Матэматычнае спадзяванне	${\displaystyle n{K \over N}}$
Мода	${\displaystyle \left\lceil {\frac {(n+1)(K+1)}{N+2}}\right\rceil -1,\left\lfloor {\frac {(n+1)(K+1)}{N+2}}\right\rfloor }$
Дысперсія	${\displaystyle n{K \over N}{N-K \over N}{N-n \over N-1}}$
Каэфіцыент асіметрыі	${\displaystyle {\frac {(N-2K)(N-1)^{\frac {1}{2}}(N-2n)}{[nK(N-K)(N-n)]^{\frac {1}{2}}(N-2)}}}$
Каэфіцыент эксцэсу	${\displaystyle \left.{\frac {1}{nK(N-K)(N-n)(N-2)(N-3)}}\cdot \right.}$ ${\displaystyle {\Big [}(N-1)N^{2}{\Big (}N(N+1)-6K(N-K)-6n(N-n){\Big )}+{}}$ ${\displaystyle {}+6nK(N-K)(N-n)(5N-6){\Big ]}}$
Утваральная функцыя момантаў	${\displaystyle {\frac {{N-K \choose n}\scriptstyle {\,_{2}F_{1}(-n,-K;N-K-n+1;e^{t})}}{N \choose n}}\,\!}$
Характарыстычная функцыя	${\displaystyle {\frac {{N-K \choose n}\scriptstyle {\,_{2}F_{1}(-n,-K;N-K-n+1;e^{it})}}{N \choose n}}}$

Гіпергеаметрычнае размеркаванне — дыскрэтнае размеркаванне імавернасцей, якое апісвае імавернасць таго, што пры выпадковым выбіранні ${\displaystyle n}$ элементаў без вяртання з генеральнай сукупнасці на ${\displaystyle N}$ элементаў, ${\displaystyle K}$ з якіх маюць пэўную ўласцівасць, ${\displaystyle k}$ элементаў выбаркі будуць мець гэтую ўласцівасць. Напрыклад калі ў скрыні знаходзіцца 10 шароў, 6 з якіх чорныя (${\displaystyle N=10}$, ${\displaystyle K=6}$), і з гэтай скрыні выпадкова выбіраецца 3 шары (${\displaystyle n=3}$), колькасць чорных шароў сярод трох выбраных будзе размеркаванай гіпергеаметрычна выпадковай велічынёй^[1]:84-85.

Азначэнне

Выпадковая велічыня ${\displaystyle X}$ мае гіпергеаметрычнае размеркаванне (запісваецца ${\displaystyle X\sim \operatorname {Hypergeometric} (N,K,n)}$), калі яе функцыя імавернасці мае выгляд^[2]

${\displaystyle p_{X}(k)=P(X=k)={\frac {{\binom {K}{k}}{\binom {N-K}{n-k}}}{\binom {N}{n}}},}$

дзе

• ${\displaystyle N}$ — памер генеральнай сукупнасці,
• ${\displaystyle K}$ — колькасць элементаў з пэўнай уласцівасцю ў генеральнай сукупнасці,
• ${\displaystyle n}$ — памер выбаркі з генеральнай сукупнасці,
• ${\displaystyle k}$ — колькасці элементаў з пэўнай уласцівасцю ў выбарцы,
• ${\displaystyle \textstyle {a \choose b}}$ — біномны каэфіцыент.

К прымае значэнні з прамежку ${\displaystyle \max(0,n+K-N)\leq k\leq \min(K,n).}$

Зноскі