Геаметрычнае размеркаванне

Геаметрычнае размеркаванне
	Фунцыя імавернасці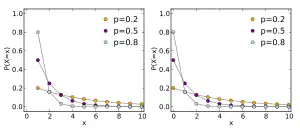
	Функцыя размеркавання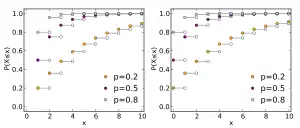
Параметры	— імавернасць поспеху (рэчаісны лік)
Носьбіт функцыі	k выпрабаванняў, дзе
Функцыя імавернасці
Функцыя размеркавання	для ,; для
Матэматычнае спадзяванне
Медыяна	; (не ўнікальная, калі — цэлы лік)
Мода
Дысперсія
Каэфіцыент асіметрыі
Каэфіцыент эксцэсу
Энтрапія
Утваральная функцыя момантаў	; для
Характарыстычная функцыя
Імавернасная ўтваральная функцыя

У тэорыі імавернасцей і статыстыцы, пад геаметрычным размеркаваннем маецца на ўвазе адно з двух дыскрэтных размеркаванняў імавернасцей:

Размеркаванне колькасці $X$ выпрабаванняў Бэрнулі, неабходных для атрымання аднаго поспеху. Колькасць выпрабаванняў прымае значэнні з мноства $\{1,2,3,\ldots \}.$ ^[1]^:82-83
Размеркаванне колькасці $Y=X-1$ няўдач да першага поспеху. Колькасць няўдач прымае значэнні $\{0,1,2,\ldots \}$ .

Азначэнне

Геаметрычнае размеркаванне задае імавернасць таго, што выпрабаванне з нумарам $k$ будзе першым паспяховым у серыі незалежных выпрабаванняў з двума магчымымі зыходамі: поспех і няўдача, дзе імавернасць поспеху кожнага выпрабавання роўная $p$ :

P(X=k)=(1-p)^{k-1}p

для k = 1, 2, 3, 4, ….

Паводле іншага азначэння, геаметрычнае размеркаванне мадэлюе колькасць няўдач да першага поспеху:

P(Y=k)=P(X=k+1)=(1-p)^{k}p

для k = 0, 1, 2, 3, ….

У абодвух выпадках, паслядоўнасць імавернасцей прадстаўляе сабой геаметрычную прагрэсію.

Характарыстыкі

Матэматычнае спадзяванне

Матэматычнае спадзяванне геаметрычнага размеркавання можна знайсці наступным чынам^[1]^:119, дзе $q=1-p$ :

\mathbb {E} [X]=\sum _{k=1}^{\infty }kpq^{k-1}=p{\frac {d}{dq}}\left(\sum _{k=1}^{\infty }q^{k}\right)=p{\frac {d}{dq}}\left({\frac {q}{1-q}}\right)=

=p{\frac {d}{dq}}\left({\frac {1}{1-q}}-1\right)={\frac {p}{(1-q)^{2}}}={\frac {1}{p}}.

Формулай сумы бясконца спадальнай геаметрычнай прагрэсіі дазваляе скарыстацца той факт, што $0\leq q<1.$

Дысперсія

Каб знайсці дысперсію, спачатку падлічым матэматычнае спадзяванне квадрата выпадковай велічыні з геаметрычным размеркаваннем^[1]^:119-120:

\mathbb {E} [X^{2}]=\sum _{k=1}^{\infty }k^{2}pq^{k-1}=p{\frac {d}{dq}}\left(\sum _{k=1}^{\infty }kq^{k}\right)=p{\frac {d}{dq}}\left({\frac {q}{(1-q)^{2}}}\right)=

p\left({\frac {1}{(1-q)^{2}}}+{\frac {2q}{(1-q)^{3}}}\right)={\frac {1}{p}}+{\frac {2q}{p^{2}}}={\frac {1+q}{p^{2}}}.

Цяпер скарыстаемся формулай для дысперсіі:

Var(X)=\mathbb {E} [X^{2}]-\mathbb {E} [X]^{2}={\frac {1+q}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {q}{p^{2}}}={\frac {1-p}{p^{2}}}.

Зноскі

1 2 3 Звяровіч Э. І., Радына А. Я. Элементы тэорыі імавернасцей. — Мінск: Беларусь, 2013. — С. 69. — ISBN 978-985-01-1043-5.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[elemienty-1] 1 2 3 Звяровіч Э. І., Радына А. Я. Элементы тэорыі імавернасцей. — Мінск: Беларусь, 2013. — С. 69. — ISBN 978-985-01-1043-5.

[1]

Фунцыя імавернасці
Функцыя размеркавання
Параметры	$0<p\leq 1$ — імавернасць поспеху (рэчаісны лік)	$0<p\leq 1$ — імавернасць поспеху (рэчаісны лік)
Носьбіт функцыі	k выпрабаванняў, дзе $k\in \{1,2,3,\dots \}$	k няўдач, дзе $k\in \{0,1,2,3,\dots \}$
Функцыя імавернасці	$(1-p)^{k-1}p$	$(1-p)^{k}p$
Функцыя размеркавання	$1-(1-p)^{\lfloor x\rfloor }$ для $x\geq 1$ , $0$ для $x<1$	$1-(1-p)^{\lfloor x\rfloor +1}$ для $x\geq 0$ , $0$ для $x<0$
Матэматычнае спадзяванне	${\frac {1}{p}}$	${\frac {1-p}{p}}$
Медыяна	$\left\lceil {\frac {-1}{\log _{2}(1-p)}}\right\rceil$ (не ўнікальная, калі $-1/\log _{2}(1-p)$ — цэлы лік)	$\left\lceil {\frac {-1}{\log _{2}(1-p)}}\right\rceil -1$ (не ўнікальная, калі $-1/\log _{2}(1-p)$ — цэлы лік)
Мода	$1$	$0$
Дысперсія	${\frac {1-p}{p^{2}}}$	${\frac {1-p}{p^{2}}}$
Каэфіцыент асіметрыі	${\frac {2-p}{\sqrt {1-p}}}$	${\frac {2-p}{\sqrt {1-p}}}$
Каэфіцыент эксцэсу	$6+{\frac {p^{2}}{1-p}}$	$6+{\frac {p^{2}}{1-p}}$
Энтрапія	${\tfrac {-(1-p)\log(1-p)-p\log p}{p}}$	${\tfrac {-(1-p)\log(1-p)-p\log p}{p}}$
Утваральная функцыя момантаў	${\frac {pe^{t}}{1-(1-p)e^{t}}},$ для $t<-\ln(1-p)$	${\frac {p}{1-(1-p)e^{t}}},$ для $t<-\ln(1-p)$
Характарыстычная функцыя	${\frac {pe^{it}}{1-(1-p)e^{it}}}$	${\frac {p}{1-(1-p)e^{it}}}$
Імавернасная ўтваральная функцыя	${\frac {pz}{1-(1-p)z}}$	${\frac {p}{1-(1-p)z}}$

Слоўнікі і энцыклапедыі	Вялікая расійская (навукова-адукацыйны партал)
Нарматыўны кантроль	Microsoft: 39947850