|
Фунцыя імавернасці 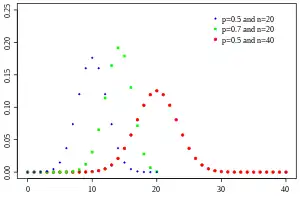 | |||
|
Функцыя размеркавання  | |||
| Абазначэнне | |||
|---|---|---|---|
| Параметры |
– колькасць выпрабаванняў – імавернасць поспеху кожнага выпрабавання – імавернасць няўдачы выпрабавання | ||
| Носьбіт функцыі | – колькасць паспяховых выпрабаванняў | ||
| Функцыя імавернасці | |||
| Функцыя размеркавання | або (рэгулярызаваная няпоўная бэта-функцыя) | ||
| Матэматычнае спадзяванне | |||
| Медыяна | або | ||
| Мода | або | ||
| Дысперсія | |||
| Каэфіцыент асіметрыі | |||
| Каэфіцыент эксцэсу | |||
| Энтрапія |
у шэнанах. Для натаў, лагарыфм мусіць быць натуральным. | ||
| Утваральная функцыя момантаў | |||
| Характарыстычная функцыя | |||
| Імавернасная ўтваральная функцыя | |||
| Інфармацыя Фішэра |
(для вызначанага ) | ||
Біномнае размеркаванне з параметрамі і — дыскрэтнае размеркаванне імавернасцей, якое апісвае колькасць паспяховых зыходаў пры правядзенні незалежных выпрабаванняў, кожнае з якіх мае два магчымыя зыходы: поспех (з імавернасцю ) і няўдача (з імавернасцю ). Кожнае такое выпрабаванне завецца выпрабаваннем Бэрнулі, а шэраг зыходаў — працэсам Бэрнулі. Для аднаго выпрабавання () біномнае размеркаванне адпавядае размеркаванню Бэрнулі[1]. Біномнае размеркаванне ляжыць у падмурку біномнага крытэрыю статыстычнай значнасці[2].
Біномнае размеркаванне часта выкарыстоўваецца для мадэлявання колькасці «паспяховых» элементаў у выбарцы з вяртаннем памерам з генеральнай сукупнасці памерам . Калі робіцца адбор без вяртання, выпрабаванні не незалежныя, і мадэляваць такую сітуацыю трэба з дапамогай гіпергеаметрычнага размеркавання. Аднак калі значна большае за , біномнае размеркаванне добра яго набліжае і таму часта выкарыстоўваецца.
Азначэнне
Функцыя імавернасці
Выпадковая велічыня , якая мая біномнае размеркаванне з параметрамі і запісваецца як Імавернасць назірання поспехаў у выпрабаваннях Бэрнулі задаецца функцыяй імавернасці:
для , дзе
— біномны каэфіцыент, ад якога і паходзіць імя размеркавання. Формула тлумачыцца наступным чынам: імавернасць назірання поспехаў роўная , а няўдач адбываюцца з імавернасцю . Пры гэтым паспяховымі могуць быць якія-кольвек з шэрагу выпрабаванняў, і існуе спалучэнняў з выпрабаванняў па .
Функцыя размеркавання
Функцыя размеркавання для мае выгляд:
дзе — цэлая частка ад .
Прыклад
Няхай манетка мае імавернасць 0.3 выпасці рэшкай. Імавернасць пабачыць 4 рэшкі пры яе шасціразовым падкіданні роўная
Характарыстыкі
Няхай Тады можна запісаць дзе кожная велічыня мае размеркаванне Бэрнулі з параметрам і ўсе незалежныя адна ад адной. Ведаючы характарыстыкі размеркавання Бэрнулі і , можна знайсці матэматычнае спадзяванне і дысперсію біномнага размеркавання[1]:
Сувязь з іншымі размеркаваннямі
Размеркаванне Бэрнулі
Размеркаванне Бэрнулі — асобны выпадак біномнага размеркавання для [1]. Іншымі словамі, велічыня мае такое ж размеркаванне, як і велічыня
Паліномнае размеркаванне
Паліномнае размеркаванне — многавымернае абагульненне біномнага. Яно дазваляе мадэляваць сітуацыі, калі магчымых зыходаў выпрабавання больш за два.