|
Шчыльнасць імавернасці 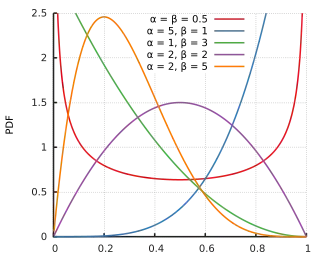 | |||
|
Функцыя размеркавання  | |||
| Абазначэнне | Beta(α, β) | ||
|---|---|---|---|
| Параметры |
α > 0 параметр формы (рэчаісны лік) β > 0 параметр формы (рэчаісны лік) | ||
| Носьбіт функцыі | або | ||
| Шчыльнасць імавернасці |
дзе , а гама-функцыя. | ||
| Функцыя размеркавання |
(рэгулярызаваная няпоўная бэта-функцыя) | ||
| Матэматычнае спадзяванне |
| ||
| Медыяна |
для | ||
| Мода |
для α, β > 1 усякае значэнне ў для α, β = 1 {0, 1} (бімадальнае) для α, β < 1 0 для α ≤ 1, β > 1 1 для α > 1, β ≤ 1 | ||
| Дысперсія |
(гл. трыгама-функцыя) | ||
| Каэфіцыент асіметрыі | |||
| Каэфіцыент эксцэсу | |||
| Энтрапія | |||
| Утваральная функцыя момантаў | |||
| Характарыстычная функцыя | (гл. канфлюэнтная гіпергеаметрычная функцыя) | ||
| Інфармацыя Фішэра | |||
| Метад момантаў |
| ||
Бэта-размеркаванне — абсалютна непарыўнае размеркаванне імавернасцей на прамежку [0, 1] або (0, 1) з двума параметрамі: альфа (α) і бэта (β), якія задаюць форму размеркавання.
Бэта-размеркаванне выкарыстоўваецца ў розных навуках для мадэлявання выпадковых велічынь, абмежаваных на пэўным інтэрвале канечнай даўжыні, напрыклад адсоткаў або прапорцый.
У баесаўскім высноўванні бэта-размеркаванне выконвае ролю спалучанага апрыёрнага для размеркавання Бэрнулі, біномнага, адмоўнага біномнага і геаметрычнага размеркаванняў.
Часам называецца бэта-размеркаваннем першага тыпу, каб адрозніць яго ад бэта-размеркавання другога тыпу. Многавымернае абагульненне бэта-размеркавання завецца размеркаваннем Дзірыхле.
Азначэнне
Шчыльнасць імавернасці

Шчыльнасць імавернасці бэта-размеркавання для 0 ≤ x ≤ 1 або 0 < x < 1 і параметраў формы α, β > 0 — ступеневая функцыя ад x і (1 − x):
дзе Γ(z) — гама-функцыя. Бэта-функцыя — нарміровачны множнік, які забяспечвае выкананне аксіёмы нармаванасці.
Калі выпадковая велічыня X мае бэта-размеркаванне з параметрамі α і β, пішуць[1][2]
Функцыя размеркавання
Функцыя размеркавання мае выгляд
дзе — няпоўная бэта-функцыя, а — рэгулярызаваная няпоўная бэта-функцыя.
Зноскі
- ↑ Rose, Colin; Smith, Murray D. (2002). Mathematical Statistics with MATHEMATICA. Springer. ISBN 978-0387952345.
- ↑ Kruschke, John K. (2011). Doing Bayesian data analysis: A tutorial with R and BUGS. Academic Press / Elsevier. p. 83. ISBN 978-0123814852.
- ↑ Berger, James O. (2010). Statistical Decision Theory and Bayesian Analysis (2nd ed.). Springer. ISBN 978-1441930743.
- ↑ Feller, William (1971). An Introduction to Probability Theory and Its Applications, Vol. 2. Wiley. ISBN 978-0471257097.