Un lletreru de neón, amosando l'enunciáu del teorema de Bayes

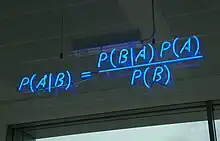
El teorema de Bayes, na teoría de la probabilidá, ye una proposición plantegada pol filósofu inglés Thomas Bayes (1702-1761)^[1] en 1760,^[2] qu'espresa la probabilidá condicional d'un eventu aleatoriu A dau B en términos de la distribución de probabilidá condicional del eventu B dau A y la distribución de probabilidá marxinal de namái A.

En términos más xenerales y menos matemáticos, el teorema de Bayes ye d'enorme relevancia yá que venceya la probabilidá d'A dau B cola probabilidá de B dau A. Esto ye, por casu, que sabiendo la probabilidá de tener un dolor de cabeza yá que se tien gripe, podría sabese (si tiense dalgún datu más), la probabilidá de tener gripe si tiense un dolor de cabeza. Amuesa esti senciellu exemplu l'alta relevancia del teorema en cuestión pa la ciencia en toles sos cañes, yá que tien vinculación íntima cola comprensión de la probabilidá d'aspeutos causales daos los efeutos reparaos.

Fórmula de Bayes

La visualización del teorema de Bayes pola superposición de dos árboles de decisión.

Con base na definición de Probabilidá condicionada llógrase la Fórmula de Bayes, tamién conocida como la Regla de Bayes:

${\displaystyle P(A_{i}|B)={\frac {P(B|A_{i})P(A_{i})}{\sum _{k=1}^{n}P(B|A_{k})P(A_{k})}}....[1]}$

Esta fórmula déxanos calcular la probabilidá condicional ${\displaystyle P(A_{i}|B)}$ de cualesquier de los eventos ${\displaystyle P(A_{i})}$, dau ${\displaystyle B}$. La fórmula ${\displaystyle [1]}$ "anició munches especulaciones filosófiques y discutinios".^[3]

Aplicaciones

El teorema de Bayes ye válidu en toles aplicaciones de la teoría de la probabilidá. Sicasí, hai un discutiniu sobre'l tipu de probabilidaes qu'emplega. N'esencia, los siguidores de la estadística tradicional namái almiten probabilidaes basaes n'esperimentos repetibles y que tengan una confirmación empírica ente que los llamaos estadísticos bayesianos dexen probabilidaes suxetives. El teorema puede sirvir entós pa indicar cómo tenemos de modificar les nueses probabilidaes suxetives cuando recibimos información adicional d'un esperimentu. La estadística bayesiana ta demostrando la so utilidá en ciertes estimaciones basaes na conocencia suxetiva a priori y el fechu de dexar revisar eses estimaciones en función de la evidencia empírica ye lo que ta abriendo nueves formes de faer conocencia. Una aplicación d'esto son los clasificadores bayesianos que son frecuentemente usaos en implementaciones de filtros de correo basura o spam, que s'afaen col usu. Otra aplicación atópase na fusión de datos, combinando información espresada en términos de densidá de probabilidá proveniente de distintos sensores.

Como observación, tiense ${\displaystyle \sum _{i=1}^{n}P(A_{i}|B)=1}$ y la so demostración resulta trivial.

Como aplicaciones puntuales:

1. El diagnósticu de cáncer.
2. Evaluación de probabilidaes mientres el desenvolvimientu d'un xuegu de bridge por Dan F. Waugh y Frederick V. Waugh.
3. Probabilidaes a priori y a posteriori.
4. Un usu revesosu na Llei de socesión de Laplace.^[4]
5. Nel testeo d'hipótesis en Ciencia Política cuando s'usa metodoloxía process tracing.

Ver tamién

• Paradoxa del cuervu
• Inferencia bayesiana

Enllaces esternos

• Calculadora n'internet
• Inferencia estadística según el modelu bayesiano, na web de la Sociedá Andaluza d'Enfermedaes Infeicioses
• Enciclopedia Stanford de filosofía
• Simulación del Teorema de Bayes con R-Project

Referencies