Les tables de multiplicar usar pa definir la operación binaria del producto pa un sistema alxebraicu. Según la correspondencia matemática:

de cuenta que a cada par ordenáu (a, b) de númberos naturales acomúñase-y un tercer natural c, que ye'l productu de los dos primeros.

Les tables de multiplicar aprender nos colexos por aciu la memorización[1] de los productos d'un númberu ente 1 y 10 polos socesivos númberos ente 1 y 10.

Conocida esta tabla y pol Algoritmu de multiplicación, pueden realizase multiplicaciones de cualquier númberu de cifres, inclusive anque estes cifres tengan parte decimal.

Tables de multiplicar

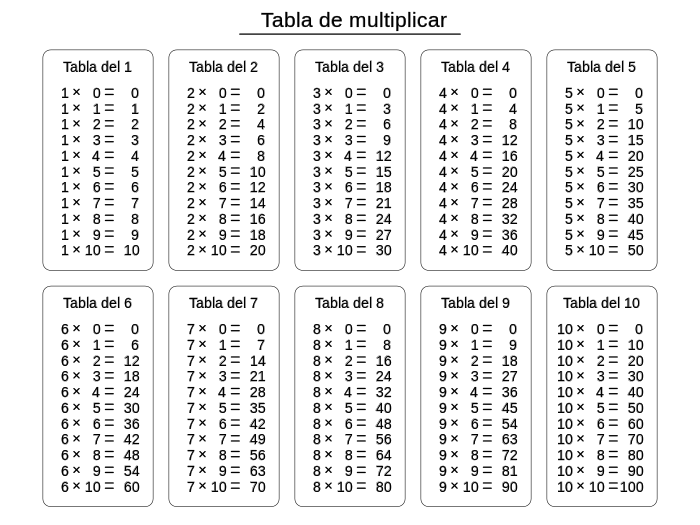
La forma tradicional de representar la tabla de multiplicar pa la so memorización o repasada ye como'l so propiu nome indica en forma de tabla.[2][3][4] Onde se multiplica, del unu al diez o del cero al diez, cada unu de los númberos. centráu

La tabla de multiplicar por coordenaes de la tabla pitagórica

Otra forma de representar la tabla de multiplicar, ye la denominada tabla pitagórica[5] (denominada asina n'honor de Pitágores), compuesta por coordenaes cartesianes (denominaes asina n'honor de Descartes). La primer fila y la primer columna contienen los númberos que se van a multiplicar (davezu, los númberos enteros hasta'l 10), y na interseición de cada fila y cada columna ta'l productu del númberu de la so fila pol númberu de la so columna.

Esta representación de la tabla de multiplicar ye más compacta que l'anterior, y dexa ver delles propiedaes de la multiplicación, la propiedá conmutativa, l'orde de los factores nun alteria'l productu, por casu el 5·3 ye igual a 3·5, esto fai qu'esti cuadru sía una matriz simétrica, los valores asitiaos a un llau otru de la diagonal que xune'l 1 y el 100, son iguales.

Esta simetría puede vese tamién al comprobar que les files y les columnes d'un mesmu númberu son iguales, si vemos la fila del trés, presenta la secuencia: 3, 6, 9, 12..., y si miramos la columna del trés tenemos la mesma secuencia 3, 6, 9..., esto ye, si camudamos les files poles columnes la tabla nun varia, esto debe a la propiedá conmutativa de la multiplicación.

La diagonal principal, recueye los cuadraos de los númberos, nesta diagonal la fila ye igual a la columna, polo que tenemos que:

La distribución de los númberos a un llau y otru d'esta diagonal tamién ye simétrica según alloñámonos d'ella.

Otres tables de multiplicar

Ábaco neperianu.

Pa exercitar el cálculu mental, dalgunos aprienden les tables de multiplicar de númberos cimeros a 10.

Nel antiguu Exiptu utilizábase'l métodu de multiplicación per duplicación, que nun riquir l'aprendizaxe de tables de multiplicar, solo precisábase saber sumar pa llograr la resultancia de multiplicaciones y divisiones.

Na antigua Babilonia, emplegábase un sistema sexaxesimal. Emplegábense profusamente tablillas col productu d'un determináu númberu, non necesariamente enteru, por 2,3,4..., hasta 60.

Tamién s'empleguen tables de multiplicar en matemátiques más avanzaes, pa definir operaciones binaries en sistemes alxebraicos como grupos, cuerpu y aniellos. Pa un exemplu, vease octoniones.

Anguaño esisten métodos matemáticos sintetizaos que dexen aprender les tables de multiplicar[6] d'una forma más senciella y amigable pal estudiante. D'esta miente amenórguense'l númberu de valores a memorizar, de 80 a 20, lo que facilita l'axilidá nel aprendizaxe pasando en poco tiempu al refuerzu.

Ver tamién

  • Multiplicación
  • Algoritmu de multiplicación
  • Multiplicación per duplicación
  • Algoritmu de Booth
  • Operaciones con polinomios

Referencies

  1. ↑ Coto, Alberto (2009). Ayuda al to fíu a entrenar la so intelixencia, 1 (en castellanu), Editorial EDAF S.L., páx. 61. ISBN 978-84-414-2099-1.
  2. ↑ de Eguilaz, Eugenio (1840). Antonio Mateis Muñoz: Tables de sumar, restar, multiplicar y estremar, 1 (en castellanu), páx. 12.
  3. ↑ Oriol y Bernadet, José (1845). José Mates: Manual d'aritmética demostrada: Al algame de los neños, 1 (en castellanu), páx. 24.
  4. ↑ Coto, Alberto (2009). Ayuda al to fíu a entrenar la so intelixencia, 1 (en castellanu), Editorial EDAF S.L., páx. 62. ISBN 978-84-414-2099-1.
  5. ↑ Tapia Felipe, Yolanda; García Anaya, Fernando José (2005). Matemátiques 2, 1 (en castellanu), Editorial Progresu SA, páx. 104. ISBN 970-641-554-8.
  6. ↑ «La nueva tabla de multiplicar» (24 de xunetu de 2013).

Enllaces esternos

Esti artículu foi traducíu automáticamente y precisa revisase manualmente
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.