El funcionamientu de la prensa hidráulica ilustra'l principiu de Pascal

En física, el principiu de Pascal o llei de Pascal, ye una llei enunciada pol físicu-matemáticu francés Blaise Pascal (1623-1662) que se resume na frase: la presión exercida sobre un fluyíu incompresible y n'equilibriu dientro d'un recipiente de parés indeformables tresmitir con igual intensidá en toles direiciones y en tolos puntos del fluyíu.^[1]

En poques pallabres, podría resumise entá ye más, afirmando que toa presión exercida escontra un fluyíu, va espardese sobre tou la sustancia de manera uniforme.^[1] El principiu de Pascal puede comprobase utilizando una esfera bueca, furada en distintos llugares y provista d'un émbolu. Al enllenar la esfera con agua y exercer presión sobre ella por aciu l'émbolu, reparar que l'agua sale por tolos furacos cola mesma velocidá y polo tanto cola mesma presión.

Tamién podemos reparar aplicaciones del principiu de Pascal nes prenses hidráuliques, nos elevadores hidráulicos, nos frenos hidráulicos, nes pontes hidráuliques y nos gatos hidráulicos.

Prensa hidráulica

Ilustración del esperimentu de Pascal del frayatu d'un barril por aciu presión nun tubu

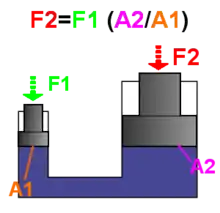
La prensa hidráulica ye una máquina complexa que dexa amplificar les fuercies y constitúi el fundamentu d'elevadores, prenses hidráuliques, frenos y munchos otros dispositivos hidráulicos .

La prensa hidráulica constitúi l'aplicación fundamental del principiu de Pascal y tamién un dispositivu que dexa entender meyor el so significáu. Consiste, n'esencia, en dos cilindros de distintu seición comunicaos ente sigo, y que'l so interior ta dafechu llenu d'un líquidu que puede ser agua o aceite. Dos émbolos de seiciones distintes afáense, respeutivamente, en cada unu de los dos cilindros, de cuenta que tean en contautu col líquidu. Cuando sobre l'émbolu de menor seición A₁ exerzse una fuercia F₁ la presión p₁ que s'anicia nel líquidu en contautu con él tresmítese íntegramente y de forma casi instantánea a tol restu del líquidu. Pol principiu de Pascal esta presión va ser igual a la presión p₂ qu'exerz el fluyíu na seición A₂, esto ye:

${\displaystyle p_{1}=p_{2}\,}$

colo que les fuercies van ser:

${\displaystyle F_{1}=p_{1}A_{1}<p_{1}A_{2}=p_{2}A_{2}=F_{2}\,,}$

con A₁ < A₂. Poro, la rellación ente la fuercia resultante nel émbolu grande cuando s'aplica una fuercia menor nel émbolu pequeñu va ser tanto mayor cuanto mayor sía la rellación ente les seiciones:

${\displaystyle F_{1}=F_{2}\left({\frac {A_{1}}{A_{2}}}\right)}$

Discutiniu llinial

Nun fluyíu les tensiones compresivas o presiones nel mesmu pueden representase por aciu un tensor de la forma:

(1)

${\displaystyle \mathbf {T} ={\begin{pmatrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{yz}&\sigma _{zz}\end{pmatrix}}}$

Eso significa qu'afitáu un puntu ${\displaystyle P\,}$ nel senu del fluyíu y considerando una direición paralela al vector unitariu ${\displaystyle \mathbf {n} }$ la fuercia por unidá d'área exercida nesi puntos según esa direición o'l vector tensión ${\displaystyle \mathbf {t} }$ vien dau por:

(2) ${\displaystyle \mathbf {t} =\mathbf {T} \mathbf {n} }$

El principiu de Pascal establez que la tensión en (2) ye independiente de la direición ${\displaystyle \mathbf {n} }$, lo cual namái asocede si'l tensor tensión ye de la forma:^[2]

(3) ${\displaystyle \mathbf {T} \approx {\begin{pmatrix}-p&0&0\\0&-p&0\\0&0&-p\end{pmatrix}}}$

onde p ye una constante que podemos identificar cola presión. De la mesma esa forma del tensor namái ye posible tenelo de forma averada si'l fluyíu ta sometíu a presiones enforma mayores que la diferencia d'enerxía potencial ente distintos partes del mesmu. Polo que'l principiu de Pascal puede formulase como: «Nun fluyíu en reposu y onde les diferencies d'altor son despreciables el tensor de tensiones del fluyíu toma la forma dada en». (3)

Sicasí, en realidá debíu al pesu del fluyíu fai que'l líquidu asitiáu na parte baxa d'un recipiente tenga una tensión llixeramente mayor que'l fluyíu asitiáu na parte cimera. De fechu si la única fuercia másica actuante ye'l pesu del fluyíu, l'estáu tensional del fluyíu a una fondura z el tensor tensión del fluyíu ye:

(4)

${\displaystyle \mathbf {T} =\mathbf {T} _{sup}+\mathbf {T} _{peso}={\begin{pmatrix}-p-\rho z&0&0\\0&-p-\rho z&0\\0&0&-p-\rho z\end{pmatrix}}}$

En vista de lo anterior podemos afirmar que «afitáu un puntu d'un fluyíu incompresible en reposu y conteníu nun recipiente so presión y indeformable, la presión del fluyíu, ye idéntica en toes direiciones, y la so tensor tensión vien dau por».(4)

Ver tamién

• Máquina simple
• Prensa hidráulica, aplicación práutica del principiu de Pascal.

Referencies

Bibliografía

• Oliver Olivella, Xavier; Agelet de Saracíbar Bosch, Carlos (2002). Mecánica de medios continuos pa inxenieros. Barcelona: Universitat Politècnica de Catalunya, páx. 346. ISBN 84-8301-412-2.

Enllaces esternos

• Wikimedia Commons acueye conteníu multimedia sobre Principiu de Pascal.
• Esperimento sobre'l principiu de Pascal