Esti artículu foi traducíu automáticamente y precisa revisase manualmente
Planu inclináu
exemplar (en) Traducir
Cambiar los datos en Wikidata
Planu inclináu y fuercies qu'actúen sobre'l sólidu.

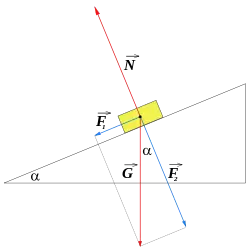
El planu inclináu ye una máquina cenciella que consiste nuna superficie plana que forma un ángulu agudu col suelu y utilízase p'alzar cuerpos a ciertu altor.

Tien la ventaya de precisase una fuercia menor que la que s'emplega si llevantamos dichu cuerpu verticalmente, anque a cuenta de aumentar la distancia percorrida y vencer la fuercia d'esfregadura.

Les lleis que rixen el comportamientu de los cuerpos nun planu inclináu fueron enunciaes per primer vegada pol matemáticu Simon Stevin, na segunda metá del sieglu XVI.

P'analizar les fuercies esistentes sobre un cuerpu asitiáu sobre un planu inclináu, hai que tener en cuenta la esistencia de dellos oríxenes nes mesmes.

  • En primer llugar tien de considerase la esistencia d'una fuercia de gravedá, tamién conocida como pesu, que ye consecuencia de la masa (M) que tien el cuerpu sofitáu nel planu inclináu y tien una magnitú de M.g con una direición vertical y representao na figura pola lletra G.
  • Esiste amás una fuercia normal (N), tamién conocida como la fuercia de reacción exercida sobre'l cuerpu pol planu de resultes de la tercer llei de Newton, atopar nuna direición perpendicular al planu y tien una magnitú igual a encomalo exercida pol planu sobre'l cuerpu. Na figura apaez representada por N y tien la mesma magnitú que F2= M.g.cosα y sentíu opuestu a la mesma.
  • Esiste finalmente una fuercia d'esfregadura, tamién conocida como fuercia de resfregón (FR), que siempres s'opón al sentíu del movimientu del cuerpu al respective de la superficie, la so magnitú depende tantu del pesu como de les carauterístiques superficiales del planu inclináu y la superficie en contautu del cuerpu qu'apurren un coeficiente d'esfregadura. Esta fuercia tien de tener un valor igual a F1=M.g.senα por que'l cuerpu caltener n'equilibriu. Nel casu en que F1 fora mayor que la fuercia d'esfregadura'l cuerpu esmuciríase escontra baxo pol planu inclináu. Por tanto pa xubir el cuerpu tien de realizase una fuercia con una magnitú qu'iguale o supere la suma de F1 + FR.

Exemplu

Imaxinemos que queremos abasnar el pesu G dende un altor 1 hasta un altor 2; siendo les posiciones 1 y 2 a les que nos referimos, les del centru de gravedá del bloque representáu na figura.

El pesu del bloque, que ye una magnitú vectorial (vertical y escontra baxo), puede descomponese en dos componentes, F1 y F2, paralelu y perpendicular al planu inclináu respeutivamente, siendo:

F1 = G sen(α)
F2 = G cos(α)

Amás, la superficie del planu inclináu xenera una fuercia d'esfregadura FR que tamién tendremos de vencer pa poder movelo. Esta fuercia ye:

FR = μ F2 = μ G cos(α), siendo μ el coeficiente d'esfregadura.

Analizando la figura, rescampla que pa consiguir mover el bloque, la fuercia (F) que tendremos d'aplicar, va ser:

F = F1 + FR = G sen(α) + μ G cos(α) = G [sen(α) + μ cos(α)]

Si en vegada del utilizar el planu inclináu, tratáramos de llevantar el bloque verticalmente, la fuercia (G) que tendríamos qu'aplicar sería la del pesu del bloque por cuenta de la fuercia de la gravedá, esto ye: G = P.

Referencies

    Enllaces esternos

    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.