Oscilador harmónicu

Dizse qu'un sistema cualesquier , mecánicu, llétricu, neumáticu, etc., ye un oscilador harmónicu si, cuando se dexa en llibertá fora de la so posición d'equilibriu, vuelve escontra ella describiendo oscilaciones sinusoidales, o sinusoidales amortiguadas en redol a dicha posición estable.

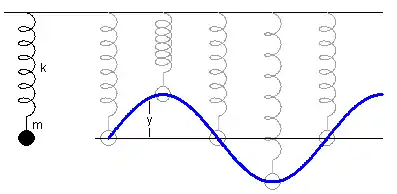
La masa colgao del resorte forma un oscilador harmónicu.

L'exemplu ye'l d'una masa colgada a un resorte. Cuando s'alloñar la masa de la so posición de reposu, el resorte exerz sobre la masa uno fuercia que ye proporcional al desequilibriu (distancia a la posición de reposu) y que ta dirixida escontra la posición d'equilibriu. Si suelta la masa, la fuercia del resorte acelera la masa escontra la posición d'equilibriu. A midida que la masa averar a la posición d'equilibriu y qu'aumenta el so velocidá, la enerxía potencial elástica del resorte tresformar en enerxía cinética de la masa. Cuando la masa llega a la so posición d'equilibriu, la fuercia va ser cero, pero como la masa ta en movimientu, va siguir y va pasar del otru llau. La fuercia inviértese y empieza a frenar la masa. La enerxía cinética de la masa va tresformándose agora n'enerxía potencial del resorte hasta que la masa párase. Entós esti procesu vuelve producise en direición opuesta completando una oscilación.

Si tou la enerxía cinética tresformar n'enerxía potencial y viceversa, la oscilación siguiría eternamente cola mesma amplitú. Na realidá, siempres hai una parte de la enerxía que se tresforma n'otra forma, por cuenta de la mafa del aire o porque'l resorte nun ye perfectamente elásticu. Con éses l'amplitú del movimientu va menguar más o menos amodo col pasu del tiempu. Empezará tratándose el casu ideal, nel cual nun hai perdes. va analizase'l casu unidimensional d'un únicu oscilador (pa la situación con dellos osciladores, vease movimientu harmónicu complexu).

Caso

Oscilador harmónicu ensin perdes

va denominase $\scriptstyle {y}$ a la distancia ente la posición d'equilibriu y la masa, a la que se-y apoderara $\scriptstyle {m}$ . va suponese que la fuercia del resorte ye puramente proporcional al desequilibriu: $\scriptstyle {F=-ky}$ (llei de Hooke). $\scriptstyle {F}$ ye la fuercia y $\scriptstyle {k}$ la constante elástica del resorte. El signu negativu indica que cuando $\scriptstyle {y}$ ye positiva la fuercia ta dirixida escontra les $\scriptstyle {y}$ negatives.

La Lleis de Newton#Segunda Llei de Newton o Llei de la Fuercia segundo llei de Newton diznos:

$F=ma=m{dv \over dt}=m{d^{2}y \over dt^{2}}$

remplazando la fuercia llogramos:

$m{d^{2}y \over dt^{2}}=-ky$

La solución d'esta ecuación diferencial ordinaria ye inmediata: les úniques funciones reales (non complexes) que la so segunda derivada ye la mesma función col signu invertíu son senu y cosenu. Los dos funciones correspuenden al mesmu movimientu. Escoyemos arbitrariamente "cosenu". La solución escríbese:

$La curva de riba da la posición del oscilador en función del tiempu. La del mediu da la velocidá. Embaxo tán les curves de les enerxíes. N'azul ta la enerxía cinética 1 2 m v 2 {\displaystyle \scriptstyle {{1 \over 2}mv^{2}}} y en colloráu la enerxía potencial del resorte 1 2 k y 2 {\displaystyle \scriptstyle {{1 \over 2}ky^{2}}}$

La curva de riba da la posición del oscilador en función del tiempu. La del mediu da la velocidá. Embaxo tán les curves de les enerxíes. N'azul ta la enerxía cinética

\scriptstyle {{1 \over 2}mv^{2}}

y en colloráu la enerxía potencial del resorte

\scriptstyle {{1 \over 2}ky^{2}}

y=A\cos(\omega t+\phi )\,

$y\,$ ye la elongación o estrema respectu al estáu d'equilibriu, les sos unidaes son les de $\scriptstyle {A}$ .
$\scriptstyle {A}$ ye l'amplitú, máxima diferencia al respective de la posición d'equilibriu.
$\scriptstyle {\omega =2\pi f}$ ye la pulsación (o frecuencia angular) y $\scriptstyle {f}$ la frecuencia.
$\scriptstyle {t}$ ye'l tiempu.
$\scriptstyle {\phi }$ ye la fase inicial (pa $\scriptstyle {t=0}$ ).

Ye fácil comprobar que'l valor de $\scriptstyle {\omega }$ ye:

\omega ={\sqrt {k \over m}}

El periodu d'oscilación ye:

T=2\pi {\sqrt {m \over k}}

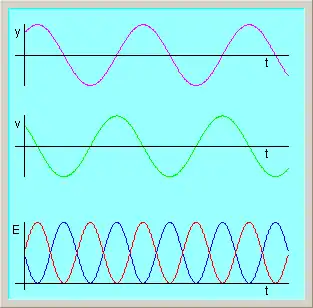
Como yá diximos, mientres un cuartu d'una oscilación la enerxía potencial tresformar n'enerxía cinética. Mientres otru cuartu, la enerxía cinética tresformar n'enerxía potencial. Na figura de la derecha trazóse la posición en función del tiempu (curva de riba), la velocidá en función del tiempu (en mediu) y les enerxíes potencial y cinéticu (embaxo).

Oscilador harmónicu amortiguado

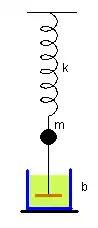
Oscilador harmónicu con amortiguador. La fuercia mafoso ye proporcional a la velocidá.

Ye'l casu d'esfregadures secos: la fuercia nun depende nin de la velocidá nin de la posición. Otra situación que se produz na realidá ye que la fuercia sía proporcional a la velocidá elevada a una potencia, entera o non. Asina asocede cuando la fuercia que frena provién de la mafa o de les perdes aerodinámiques. va tratase namái'l casu más simple, esto ye, cuando la fuercia sía proporcional a la velocidá. Nesti casu la fuercia va ser:

F_{f}=-bv=-b{dy \over dt}

Onde $\scriptstyle {b}$ ye un coeficiente que mide l'amortiguamientu por cuenta de la mafa. Si $\scriptstyle {b}$ ye pequeñu, el sistema ta pocu amortiguado. Nótese'l signu negativu qu'indica, como antes, que si la velocidá ye positiva, la fuercia tien la direición cimera opuesta a la velocidá de la partícula. Con esti términu complementariu la ecuación diferencial del sistema ye:

m{d^{2}y \over dt^{2}}=-ky-b{dy \over dt}

Trátase d'una ecuación diferencial ordinaria, llinial, de segundu orde^[1] (contién derivaes segundes) y homoxénea (nun hai términu independiente de $y$ ). Tien tres tipos de soluciones según el valor de $\scriptstyle {b^{2}-4km}$ :

Si $\scriptstyle {b^{2}-4km>0}$ el sistema ta sobreamortiguado (amortiguamientu fuerte o supercrítico)
Si $\scriptstyle {b^{2}-4km=0}$ el sistema tien amortiguamientu críticu.
Si $\scriptstyle {b^{2}-4km<0}$ el sistema bazcuya con amplitú decreciente (amortiguamientu débil o subcrítico)

Oscilador sobreamortiguado

Posición en función del tiempu d'un oscilador harmónicu amortiguado.

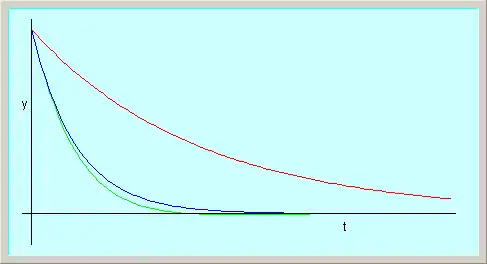
curva azul: amortiguamientu críticu.
curva colorada: amortiguamientu doble que'l críticu.
curva verde: amortiguamientu igual a 90% del amortiguamientu críticu.

Nesti casu'l sistema nun ye realmente un oscilador, yá que nun bazcuya. La solución ye de la forma:

y=A_{1}y^{\lambda _{1}t}+A_{2}y^{\lambda _{2}t}

onde los coeficientes de les esponenciales son menores que cero y reales (polo que nun hai oscilación):

\lambda _{1}={-b-{\sqrt {b^{2}-4km}} \over 2m}

y :: $\lambda _{2}={-b+{\sqrt {b^{2}-4km}} \over 2m}$ $\scriptstyle {A_{1}}$ y $\scriptstyle {A_{2}}$ dependen de les condiciones iniciales (esto ye, de la situación del sistema pa $\scriptstyle {t=0}$ ). La posición nun ye trémbole y tiende escontra la posición d'equilibriu de manera asintótica. Los dos esponenciales decrecientes de les soluciones tienen constantes de tiempu distintos. Una ye pequeña $\scriptstyle {1/\lambda _{1}}$ y correspuende a la rápida cancelación del efeutu de la velocidá inicial. La segunda $\scriptstyle {1/\lambda _{2}}$ ye más grande y describe el lentu enclín escontra la posición d'equilibriu.

Oscilador con amortiguamientu críticu

Esti casu ye la llende ente un sistema trémbole y uno non trémbole. Asocede cuando :: $b^{2}=4km\,$ La solución única ye:

y=A_{1}y^{-{b \over 2m}t}+A_{2}te^{-{b \over 2m}t}

como antes, $\scriptstyle {A_{1}}$ y $\scriptstyle {A_{2}}$ son constantes que dependen de les condiciones iniciales.

L'amortiguamientu críticu correspuende al enclín más rápidu escontra la situación d'equilibriu cuando nun devasa esa posición. Si menguar un pocu l'amortiguamientu'l sistema avérase más rápido a la posición d'equilibriu, pero devasando la posición bazcuya en redol a esi puntu (tomando valores positivos y negativos).

Oscilador con amortiguamientu débil

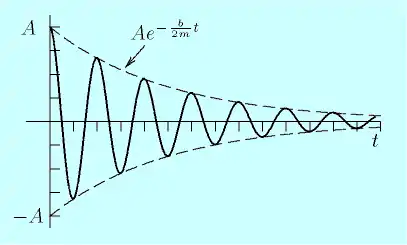
Oscilaciones amortiguadas. L'amplitú de la sinusoide ta controlada pola esponencial.

Nesti casu, que ye más interesante, tenemos un oscilador que bazcuya alredor de la posición d'equilibriu con amplitú decreciente. Asocede cuando:

b^{2}<4km\,

La solución ye:

y=Ae^{-{b \over 2m}t}\cos(\omega t+\phi )

como antes, $\scriptstyle {A}$ y $\scriptstyle {\phi }$ son constantes que dependen de les condiciones iniciales. La pulsación ye:

\omega ={\sqrt {{k \over m}-\left({b \over 2m}\right)^{2}}}

La pulsación del sistema amortiguado ye un pocu menor que la pulsación del sistema non amortiguado $\scriptstyle {\omega _{\circ }={\sqrt {k \over m}}}$ porque la fuercia que lo amortigua, frena la masa y retárdalo.

La oscilación del sistema ta descrita por una sinusoide de frecuencia $\scriptstyle {f={1 \over 2\pi }{\sqrt {{k \over m}-\left({b \over 2m}\right)^{2}}}}$ que la so amplitú ta multiplicada por una esponencial decreciente que la so constante de tiempu ye $\scriptstyle {\tau ={2m \over b}}$ .

Factor calidable Q

Nun sistema pocu amortiguado ye interesante definir el factor calidable (Quality factor n'inglés) o a cencielles Q como:

Q={{\sqrt {km}} \over b}

esta cantidá ye igual a $2\pi$ vegaes l'inversu de les perdes relatives d'enerxía per periodu. Asina, un sistema que pierde 1% d'enerxía a cada ciclu, va tener un Q de 628. Más interesante, Q ye tamién $\textstyle {\pi }$ vegaes el númberu d'oscilaciones que'l sistema fai mientres la so amplitú estremar por un factor $\textstyle {y}$ . Si puede aceptase un aproximamientu más porcaz, Q ye 3 vegaes el númberu d'oscilaciones qu'un sistema fai mientres la so amplitú cai a 1/3 de l'amplitú inicial.

Como exemplos, el Q d'un vehículu colos amortiguadores en bon estáu ye un pocu más grande que 1. El Q d'una cuerda de guitarra ye de dellos miles. El Q de los cristales de cuarzu utilizaos en electrónica como referencia de frecuencia ye l'orde de 1 millón. Una copa de vidriu ordinariu tien un Q muncho más pequeñu qu'una copa de vidriu de plomu (cristal).

Oscilaciones forzaes

Podemos empecipiar el movimientu un oscilador harmónicu moviéndolo de la so posición d'equilibriu y abandonándolo a la so oscilación llibre (ver párrafos precedentes).

Alternativamente, podemos aplica-y una fuercia que la so intensidá varie de manera sinusoidal col tiempu. Nesta situación, la ecuación diferencial llinial ye inhomogénea. La solución a esti tipu d'ecuación ta formada por dos términos: la solución xeneral del sistema homoxéneu más una solución particular del casu inhomogéneo.^[2] Poro, la solución ta formada por dos partes, una parte transitoria (que s'anula pasáu ciertu tiempu), similar a les que vimos nos párrafos precedentes, más una parte estacionaria. La solución de la parte transitoria ye la mesma la que yá vimos (ecuación homoxénea). Les úniques diferencies son les condiciones inicial y final, que nun son idéntiques. Vamos interesanos a la solución estacionaria. Na ecuación diferencial del sistema hai qu'añader la fuercia sinusoidal:

m{d^{2}y \over dt^{2}}+b{dy \over dt}+ky=F_{m}\cos(\omega t)

Pa resolver esta ecuación ye más interesante utilizar el mesmu métodu que n'lletricidá y electrónica. Pa ello, añader a encomalo real una fuercia imaxinaria $\scriptstyle {jF_{m}{\text{sen}}(\omega t)}$ . Como n'electrónica, utilízase $\scriptstyle {j^{2}=-1}$ en llugar de i. Agora la ecuación a resolver ye:

m{d^{2}y \over dt^{2}}+b{dy \over dt}+ky=F_{m}e^{j\omega t}

Pero de xacíu, como n'lletricidá, namái la parte real de y va ser d'interés. La solución ye inmediata:

y=Ae^{j\omega t}\,

Si derívase esta espresión y sustitúyese na ecuación diferencial, atópase'l valor d'A:

A={F_{m} \over k-m\omega ^{2}+jb\omega }

Pero A pue escribise como $\scriptstyle {A=\rho y^{j\phi }}$ y la solución de $\scriptstyle {y}$ complexa ye:

y=\rho y^{j\phi }y^{j\omega t}=\rho y^{j\left(\omega t+\phi \right)}

El valor de $\scriptstyle {y}$ real ye la parte real de la espresión precedente:

y=\rho \cos \left(\omega t+\phi \right)

onde $\scriptstyle {\rho }$ ye'l módulo de $\scriptstyle {A}$ y $\scriptstyle {\phi }$ el so argumentu:

\rho =\left|A\right|=\left|{F_{m} \over k-m\omega ^{2}+jb\omega }\right|

\phi =\arg \left(A\right)=\arg \left({F_{m} \over k-m\omega ^{2}+jb\omega }\right)

Como n'lletricidá, l'ángulu $\scriptstyle {\phi }$ da'l desfase del movimientu con al respective de la fuercia esterno. Si $\scriptstyle {\phi }$ ye positivu, el movimientu ta en meyora de fase y si $\scriptstyle {\phi }$ ye negativu'l movimientu ta en retardo de fase. Nesti casu'l desfase va ser siempres negativu.

Respuesta en frecuencia

L'amplitú de les oscilaciones forzaes va depender, poques gracies, de l'amplitú de la fuercia esterno. Pero pa una mesma amplitú de la fuercia, l'amplitú de la oscilación va depender tamién de la frecuencia. Veamos como varia l'amplitú $\scriptstyle {\rho }$ con $\scriptstyle {\omega }$ . Utilizando la definición de frecuencia propia del sistema (ensin amortiguamientu nin fuercia esterno):

Respuesta en frecuencia d'un oscilador harmónicu. A la frecuencia de resonancia, l'amplitú ye Q vegaes más grande qu'a bien baxa frecuencia.

\omega _{\circ }={\sqrt {k \over m}}

puede escribise:

A={F_{m} \over k}{1 \over 1-\left({\omega  \over \omega _{o}}\right)^{2}+j{\omega  \over \omega _{o}}{\sqrt {b^{2} \over km}}}

Si amás utilízase la definición de $\scriptstyle {Q={{\sqrt {km}} \over b}}$ , llógrase:

A={F_{m} \over k}{1 \over 1-\left({\omega  \over \omega _{o}}\right)^{2}+j{\omega  \over \omega _{o}}{1 \over Q}}

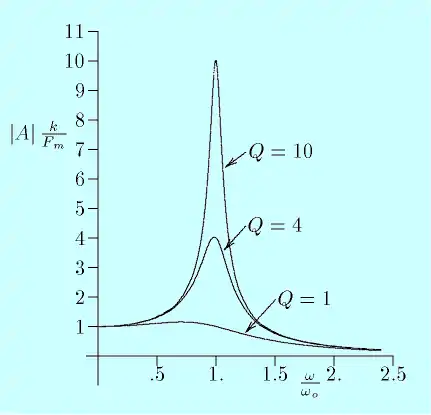
Nel dibuxu de derecha representóse l'amplitú de la oscilación forzada en función de la frecuencia pa dellos valores del factor calidable Q. A bien baxa frecuencia l'amplitú ye la mesma que si la fuercia fora estática $\scriptstyle {F_{m}=ka}$ , y el sistema va bazcuyar ente les posiciones $\scriptstyle {F_{m} \over k}$ y $\scriptstyle {-{F_{m} \over k}}$ . Cuando la frecuencia aumenta, l'amplitú tamién, algamando un máximu cuando la frecuencia d'escitación ye igual a la frecuencia propia del sistema. A esa frecuencia propia tamién se-y llama frecuencia de resonancia. Tamién se diz qu'un sistema escitáu a una frecuencia próxima a la frecuencia de resonancia "resona" o "entra en resonancia". A la frecuencia de resonancia, l'amplitú de les oscilaciones va ser Q vegaes más grande que la que se llogra en baxa frecuencia.

L'anchu del picu de resonancia a mediu altor, ye dicir cuando l'amplitú ye igual a la metá del máximu, ye igual a la frecuencia de resonancia estremada por Q. Esi anchu tamién se llama banda pasante.

Oscilador forzáu y caos

L'oscilador harmónicu non alteriáu nuna dimensión ye un exemplu de sistema integrable, con comportamientu regular. Sicasí, l'oscilador harmónicu venáu puede presentar un comportamientu teoría del caos caóticu^[3] carauterizáu por un atractor estrañu. Por casu nel casu d'una perturbación de tipu $x^{3}\;$ la ecuación de movimientu ye:

${\frac {d^{2}x}{dt^{2}}}+a{\frac {dx}{dt}}+\omega ^{2}x+\varepsilon \omega ^{2}x^{3}=b\cos(\omega t)$

Esti sistema ye non integrable y el movimientu tiende rápido escontra'l llamáu atractor de Duffing.^[4]

Oscilador de van der Pol

Comportamientu Teoría del caos caóticu nel oscilador de van der Pol con escitación sinusoidal. μ = 8.53, ente que la escitación esterna tien amplitú A = 1.2 y frecuencia angular ω = 2π / 10.

El oscilador de van der Pol ye un casu especial d'oscilador con amortiguamientu non llinial, que respuende a la ecuación:

{d^{2}x \over dt^{2}}-\mu (1-x^{2}){dx \over dt}+x=0

Foi descritu per primer vegada en 1935 por Balthasar van der Pol^[5] y presenta comportamientu caóticu.

Oscilador harmónicu torsional

Importancia en física

Considérese'l casu d'un cuerpu sometíu a una fuercia unidimensional: $F(y)$ . Desenvolviendo dicha fuercia en serie de Taylor alredor del puntu d'equilibriu ( $y=0$ ):

F(y)=F(y=0)+y\left({\frac {dF}{dy}}\right)_{y=0}+{1 \over 2}y^{2}\left({\frac {d^{2}F}{dy^{2}}}\right)_{y=0}+...

Como l'orixe ye'l puntu d'equilibriu, el primer términu del desenvolvimientu ye nulu. Si les oscilaciones en redol a $y=0$ son lo suficientemente pequeñes, unu puede quedase col aproximamientu llinial y despreciar los términos d'orde cimeru:

F(y)\simeq \ y\left({\frac {dF}{dy}}\right)_{y=0}

Llamándo-y $k$ a la derivada de la fuercia, llograr de nuevu la fuercia recuperador de Hooke. Equí anicia la importancia del oscilador harmónicu: supón un primer aproximamientu pal estudiu d'un sistema cuando se producen pequeñes oscilaciones en redol a la so posición (o estáu) d'equilibriu.^[6]

Exemplos

Circuito LC

Circuitu LC ensin perdes

Circuitu LC ensin perdes.

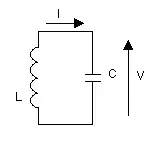
Na figura de la derecha dibuxóse un circuitu trémbole LC (una bobina y un condensador) ideal, ye dicir ensin perdes.

Supóngase que, na situación inicial, el condensador ta cargáu a una tensión V y que nesi momentu conéctase la inductancia. La tensión presente nes estremidaes de la inductancia va faer apaecer una corriente de sentíu inversu a la de la flecha del dibuxu, que va aumentar col tiempu. A midida que el condensador suministra corriente a la inductancia, descárgase y la tensión mengua. L'amenorgamientu de la tensión fai que la corriente aumente menos rápido. La situación continua asina, cola tensión del condensador que mengua cada vez más rápido (porque la corriente aumenta) y la corriente qu'aumenta más amodo (porque la tensión mengua). Llega un momentu nel cual el condensador ta dafechu descargáu y la corriente llegó a un máximu. Agora la corriente sigue circulando porque la inductancia imponer. El condensador empieza a cargase nel otru sentíu y fai apaecer una tensión nos bornes de la inductancia que fai menguar la corriente. La situación sigue de la siguiente manera: el condensador va cargándose cada vez más amodo (porque la corriente mengua), ente que la corriente va menguando cada vez más rápido (porque la tensión inverso aumenta). Asina, llegar a la situación na cual la corriente anúlase y la tensión del condensador ye máxima y del mesmu valor que la tensión inicial, pero con sentíu opuestu. La situación ye análoga a la d'una masa sostenida por un resorte. La inductancia xuega'l papel de la masa. La masa tien inercia y torga que'l movimientu camude sópito. La inductancia torga que la corriente camude sópito. Veamos les ecuaciones.

El comportamientu llétricu del condensador ta descritu pola ecuación: $\scriptstyle {I=C{dV \over dt}}$ . El de la inductancia ta descritu por $\scriptstyle {V=L{di \over dt}}$ . Como nel esquema $\scriptstyle {I}$ ye positivu cuando sale del llau positivu de la inductancia, hai qu'amestar un signu negativu: $\scriptstyle {V=-L{di \over dt}}$ . Tiense, pos, esti sistema d'ecuaciones diferenciales:

I=C{dV \over dt}

V=-L{di \over dt}

Pa esaniciar $\scriptstyle {I}$ , basta derivar la primer ecuación, pa remplazar la derivada d'I na segunda:

V=-LC{d^{2}V \over dt^{2}}

que puede escribise como:

L{d^{2}V \over dt^{2}}=-{1 \over C}V

Esta ecuación ye la mesma que la de la masa con un resorte. $\scriptstyle {V}$ ye equivalente a la posición $\scriptstyle {y}$ . $\scriptstyle {L}$ ye equivalente a la masa $\scriptstyle {m}$ y $\scriptstyle {1 \over C}$ ye equivalente a la constante del resorte $\scriptstyle {k}$ .

La solución ye:

V=V_{\circ }\cos(\omega t+\phi )

con

\omega ={1 \over {\sqrt {LC}}}

Como de costume, $\scriptstyle {V_{\circ }}$ y $\scriptstyle {\phi }$ dependen de les condiciones iniciales.

Circuitu LC con perdes

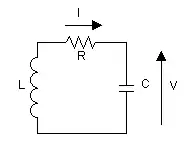
Circuitu LC con perdes. La resistencia da cuenta de toes la perdíes posibles.

L'esquema de la derecha representa un circuitu trémbole LC con perdes. Les perdes tán representaes poles perda nuna resistencia. Nun circuitu real, les perdes provienen de resistencies en serie como la dibuxada. Diches resistencies pueden tar nel esterior de la inductancia o del condensador, pero tamién pueden ser resistencies internes d'esos componentes. Tamién puede haber resistencies en paralelu, perdíes nel dieléctricu del condensador o nel nucleu de la bobina (si ye ferromagnético). Tamién puede haber perdes por radiación d'ondes electromagnétiques. La resistencia va faer que la tensión sobre la bobina sía distinta de la tensión sobre'l condensador. La corriente creada va ser menor que si nun hubiera perdes y cuando la corriente cargue de nuevu'l condensador, la tensión a la cual va llegar va ser menor. Pela so parte, l'amplitú va menguar y va tender escontra cero. La ecuación del nuevu sistema ye:

L{d^{2}V \over dt^{2}}+R{dV \over dt}+{1 \over C}V=0

La ecuación ye la mesma que la d'una masa con un resorte y con un amortiguador. Esta vegada $\scriptstyle {R}$ ye l'equivalente del coeficiente d'esfregadura $\scriptstyle {b}$ . La solución ye:

V=V_{\circ }y^{-{R \over 2L}t}\cos(\omega t+\phi )

con

\omega ={\sqrt {{1 \over LC}-\left({R \over 2L}\right)^{2}}}

y :: $Q={\sqrt {L \over RC}}={\omega _{\circ }L \over R}={R \over \omega _{\circ }C}$ onde $\scriptstyle {\omega _{\circ }={1 \over {\sqrt {LC}}}}$ ye la frecuencia propia del circuitu (ensin perdes).

Oscilaciones forzaes d'un circuitu LC con perdes

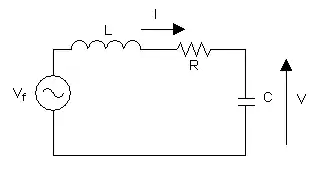
Circuitu LRC atacáu por un xenerador sinusoidal.

L'esquema de la derecha amuesa un xenerador conectáu a un circuitu LC en serie. Si la tensión del xenerador ye $\scriptstyle {V_{f}\cos(\omega t)}$ , la ecuación ye:

LC{d^{2}V \over dt^{2}}+RC{dV \over dt}+V=V_{f}\cos(\omega t)

La espresión puede reescribise, dándo-y un aspeutu similar a les formes precedentes:

L{d^{2}V \over dt^{2}}+R{dV \over dt}+{1 \over C}V={V_{f} \over C}\cos(\omega t)

Como nel exemplu mecánicu, en réxime estacionariu la solución ye:

V=V_{\circ }\cos(\omega t+\phi )

onde :: $V_{\circ }=V_{f}\left|{1 \over 1-\left({\omega \over \omega _{\circ }}\right)^{2}+j{1 \over Q}{\omega \over \omega _{\circ }}}\right|$ y :: $\phi =Arg\left({1 \over 1-\left({\omega \over \omega _{\circ }}\right)^{2}+j{1 \over Q}{\omega \over \omega _{\circ }}}\right)$ $\scriptstyle {\omega _{\circ }}$ y $\scriptstyle {Q}$ son los mesmos que nel párrafu precedente. L'amplitú de la tensión de salida ye máxima a la resonancia (cuando $\scriptstyle {\omega =\omega _{\circ }}$ ) y vale $\scriptstyle {Q}$ vegaes la tensión d'entrada.

Oscilador harmónicu cuánticu

Funciones d'onda pa los primeros seis autoestados, n = 0 a 5. La exa horizontal amuesa la posición y n'unidaes (h/2πmω)^1/2. Les gráfiques tán ensin normalizar.

Densidá de probabilidá de los primeres autoestados (dimensión vertical, colos de menor enerxía na parte inferior) pa les distintes llocalizaciones espaciales (dimensión horizontal).

Susodichamente, l'oscilador harmónicu puede emplegase pa estudiar sistemes que realicen pequeñes oscilaciones en redol a una posición d'equilibriu. En particular, el oscilador harmónicu cuánticu puede emplegase pa estudiar les oscilaciones de los átomos d'una molécula diatómica, como la d'hidróxenu, H₂, o la de cloruru d'hidróxenu, HCl.^[7]

L'oscilador harmónicu ye unu de los casos nos que puede llograse una solución analítica senciella de la ecuación de Schrödinger. Nesta situación, l'hamiltoniano de la partícula considerada va tar descritu por:

{\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}y^{2}

Nótese que pal casu de molécules diatómicas, la masa $m$ sería, en realidá, la masa amenorgada del sistema. Vese claramente que'l primera sumando ye un términu cinéticu, ente que'l segundu ye l'harmónicu. Como'l hamiltoniano nun depende del tiempu, namái resta resolver la ecuación de Schrödinger independiente del tiempu, con cuenta de topar los autoestados de la enerxía $Y$ :

{\hat {H}}|\psi (y)\rangle =Y|\psi (y)\rangle

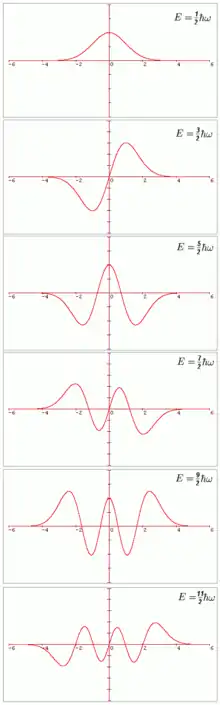
Puede demostrase que les funciones d'onda, $\psi (y)$ , que'l so módulu al cuadráu describe la densidá de probabilidá de que la partícula tenga una determinada posición $y$ , son el productu d'esponenciales polos polinomios de Hermite. La figura de la derecha amuesa la forma de diches funciones pa los seis autoestados con enerxía más baxa (l'estáu de menor enerxía ye'l que figura na parte cimera de la mesma). En particular, la enerxía del nivel n-ésimo va ser:

Y_{n}=\hbar \omega \left(n+{1 \over 2}\right)\qquad n=0,1,2,...

onde $\scriptstyle {\hbar }$ ye la constante de Planck.

Ye importante señalar un par de fechos:

Los niveles d'enerxía atópense cuantizados, esto ye, namái pueden tomar una serie de valores discretos.
El nivel mínimu d'enerxía nun ye cero, sinón $\scriptstyle {(1/2)\hbar \omega }$ . Nótese que la función d'onda de dichu estáu amuesa que la partícula nun s'atopa en tou momentu na posición d'equilibriu $y=0$ .

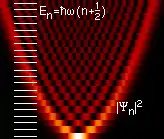
Na segunda figura, amuésense les densidaes de probabilidá espacial de la partícula pa los distintos autoestados. Nótese qu'a midida que crez la enerxía del autoestado consideráu (esto ye, l'orde $n$ ), les distribuciones de probabilidá tienden a concentrase nos puntos de torna, o máxima amplitú. Esta situación ye la que se da nel casu clásicu, si definir pa él una densidá de probabilidá inversamente proporcional a la velocidá de la partícula en cada puntu.^[8] Por tanto, cumplir el principiu de correspondencia (esto ye, pueden predicise los resultaos que se llograríen na llende clásica).

Ver tamién

Pendilexu
Pendilexu cicloidal
Pendilexu de Newton
Pendilexu de Pohl
Pendilexu de torsión
Pendilexu físicu
Pendilexu simple

Referencies

↑ Simmons, capítulu 3
↑ Simmons, páxines 84-87
↑ T.N. Palmer (1995): "A local deterministic model of Quantum Spin Measurement", Proceedings: Mathematical and Physical Sciences, Volume 451, Issue 1943, páxs. 585-608
↑ Atractor de Duffing
↑ Cartwright, M.L., "Balthazar van der Pol", J. London Math. Soc., 35, 367-376, (1960).
↑ Marion, páxines 103 y 104
↑ Tipler, páxina 1190
↑ Guillén, páxines 114 y 115

Bibliografía

Feynman, Leighton and Sands. Lectures on

physics. Addison-Wesley. ISBN 0-8053-9045-6.

R. Resnick and D. Halliday (1996). Physics. John Wiley & Sons. ISBN 0-471-83202-2.
Marion, Jerry B. (1996). Dinámica clásica de les partícules y sistemes. Barcelona: Ed. Reverté. ISBN 84-291-4094-8.
Simmons, George F. (1999). Ecuaciones Diferenciales. Con aplicaciones y notes históriques. Aravaca (Madrid): McGraw-Hill. ISBN 84-481-0045-X.
Tipler, Paul A. (2000). Física pa la ciencia y la teunoloxía (volume 2). Barcelona: Ed. Reverté. ISBN 84-291-4382-3.
Sánchez Guillén, Joaquín. Braun, Mijail A. (1993). Física cuántica. Madrid: Alianza Editorial. ISBN 84-206-8145-8.

Enllaces esternos

Artículu na Wikipedia en francés sobre'l pendilexu compuestu *

Hyperphysics (sitiu n'inglés)

Oscilador harmónicu cuánticu en Hyperphysics.
Páxina (n'inglés) con animaciones avera del oscilador harmónicu, el pendilexu simple y otros fenómenos.
Páxina (n'inglés) con animaciones d'oscilaciones y ondes.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Simmons, capítulu 3

[2] Simmons, páxines 84-87

[3] T.N. Palmer (1995): "A local deterministic model of Quantum Spin Measurement", Proceedings: Mathematical and Physical Sciences, Volume 451, Issue 1943, páxs. 585-608

[4] Atractor de Duffing

[Biography-5] Cartwright, M.L., "Balthazar van der Pol", J. London Math. Soc., 35, 367-376, (1960).

[6] Marion, páxines 103 y 104

[7] Tipler, páxina 1190

[8] Guillén, páxines 114 y 115

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]