Númberu enteru

Númberu enteru
	tipu de númberu
	número con representación decimal finita (es) , númberu real, entero gaussiano (es) y entero p-ádico (es)

La resta de dos númberos naturales nun ye un númberu natural cuando'l sustraendo ye mayor que'l minuendu, sinón que'l so valor ye negativu: na imaxe, solo pueden sustraese 3 plátanos, polo que s'apunta un plátanu debíu» o «negativu» (en colloráu).

Un númberu enteru ye un elementu del conxuntu numbéricu que contién los númberos naturales $\mathbb {N} =\{1,2,3,4,\cdots \}$ , los sos opuestos y el cero.^[1] Los enteros negativos, como −1 o −3 (lléense «menos unu», «menos trés», etc.), son menores que cero y tolos enteros positivos. Pa resaltar la diferencia ente positivos y negativos, puede escribise un signu «más» delantre de los positivos: +1, +5, etc. Y si nun s'escribe signu al númberu asumir que ye positivu.

El conxuntu de tolos númberos enteros representar pola lletra $\mathbb {Z} =\{...,-3,-2,-1,0,+1,+2,+3,\,...\}$ lletra inicial del vocablu alemán Zahlen («númberos», pronunciáu [ˈtsaːlən]).

Na recta numbérica atopamos los númberos negativos a la izquierda del cero y a la so derecha los positivos.

Los númberos enteros pueden sumarse, restarse, multiplicase y estremase, siguiendo'l modelu de los númberos naturales añadiendo unes normes pal usu del signu.

Los númberos enteros estienden la utilidá de los númberos naturales pa cuntar coses. Pueden utilizase pa contabilizar perdes: si nun colexu entren 80 alumnos nuevos de primer cursu un ciertu añu, pero hai 100 alumnos d'últimu cursu que pasaron a educación secundaria, en total va haber 100 − 80 = 20 alumnos menos; pero tamién puede dicise que dichu númberu aumentó en 80 − 100 = −20 alumnos.

Ciertes magnitúes como la temperatura o l'altor usen valores per debaxo del cero. L'altor del Everest ye 8848 metros percima del nivel del mar, y otra manera, la vera del mar Muertu ta 423 metros per debaxo del nivel del mar; esto ye, el so altor puede espresase como −423 m.

Introducción

Los númberos negativos son necesarios pa realizar operaciones como:

3 − 5 = ?

Cuando'l minuendu ye más pequeñu que'l sustraendo, la resta nun puede realizase con númberos naturales. Sicasí, hai situaciones nes que ye útil el conceutu de númberos negativos, como por casu al falar de ganancies y perdes:

Exemplu: Un home xuega a la ruleta dos díes siguíos. Si'l primeru gana 2000 pesos y a otru día pierde 1000, l'home ganó en total 2000 − 1000 = $ 1000. Sicasí, si'l primer día gana 500 y al siguiente pierde 2000, dizse que perdió en total 2000 − 500 = $ 1500. La espresión usada camuda en cada casu: ganó en total o perdió en total, dependiendo de si les ganancies fueron mayores que les perdes o viceversa. Estos dos posibilidaes pueden espresase utilizando'l signu de los númberos negativos (o positivos): nel primer casu ganó en total 2000 − 1000 = + $ 1000 y nel segundu ganó en total 500 − 2000 = − $ 1500. Asina, entiéndese qu'una perda ye una ganancia negativa.

Númberos con signu

Los númberos naturales 1, 2, 3,... son los númberos ordinarios que s'utilicen para cuntar. Al añader un signu menos («−») delantre llógrense los númberos negativos:

Un númberu enteru negativu ye un númberu natural como 1, 2, 3, etc. precedíu d'un signu menos, «−». Por casu −1, −2, −3, etcétera. Lléense «menos 1», «menos 2», «menos 3»,...

Amás, pa estremalos meyor, a los númberos naturales añader un signu más («+») delantre y llámase-yos númberos positivos.

Un númberu enteru positivu ye un númberu natural como 1, 2, 3,... precedíu d'un signu más. «+».

El cero nun ye positivu nin negativu, y puede escribise con signu más o menos o ensin signu indistintamente, yá que sumar o restar cero ye igual a nun faer nada. Toa esta coleición de númberos son los llamaos enteros».

Los númberos enteros son el conxuntu de tolos númberos enteros con signu (positivos y negativos) xunto col 0. Represéntase-yos pola lletra $Z$ , tamién escrita en «negrina de cayuela» como $ℤ$ :

$\mathbb {Z} =\{\dots ,-2,-1,0,+1,+2,\dots \}$

La recta numbérica

Los númberos enteros negativos son más pequeños que tolos positivos y que'l cero. Esto ye, tou númberu que s'atopa allugáu a la derecha ye mayor que'l númberu que s'atopa allugáu a la izquierda. Pa entender como tán ordenaos utilízase la recta numbérica: centru Ver con esta representación que los númberos negativos son más pequeños cuanto más a la izquierda, esto ye, cuanto mayor ye'l númberu tres el signu. A esti númberu llámase-y el valor absolutu:

El valor absolutu d'un númberu enteru ye la distancia qu'hai del orixe (cero) hasta un puntu dau. El valor absolutu de 0 ye a cencielles 0. Representar por dos barras verticales «||».

Exemplos. |+5| = 5 , |−2| = 2 , |0| = 0.

L'orde de los númberos enteros puede resumise en:

El orde de los númberos enteros defínese como:

Daos dos númberos enteros de signos distintos, $+ a$ y $- b$ , el negativu ye menor que'l positivu: $- b < + a$ .

Daos dos númberos enteros col mesmu signu, el menor de los dos númberos ye:
El de menor valor absolutu, si'l signu común ye «+».

El de mayor valor absolutu, si'l signu común ye «−».

El cero, 0, ye menor que tolos positivos y mayor que tolos negativos.

Exemplos. +23 > −56 , +31 < +47 , −15 < −9 , 0 > −36

Operaciones con númberos enteros

Los númberos enteros pueden sumarse, restarse, multiplicase y estremase, igual que puede faese colos númberos naturales.

Suma

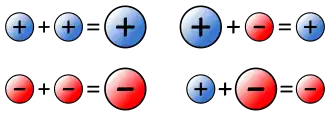
Nesta figura, el valor absolutu y el signu d'un númberu representar pol tamañu del círculu y el so color.

Na suma de dos númberos enteros, determinar por separáu'l signu y el valor absolutu de la resultancia.

Pa sumar dos númberos enteros, determinar el signu y el valor absolutu de la resultancia de la siguiente manera:

Si ambos sumandos tienen el mesmu signu: esi ye tamién el signu de la resultancia, y el so valor absolutu ye la suma de los valores absolutos de los sumandos.

Si ambos sumandos tienen distintu signu:
El signu de la resultancia ye'l signu del sumandu con mayor valor absolutu.

El valor absolutu de la resultancia ye la diferencia ente'l mayor valor absolutu y el menor valor absolutu, d'ente los dos sumandos.

Exemplos. (+21) + (−13) = +8 , (+17) + (+26) = +43 , (−41) + (+19) = −22 , (−33) + (−28) = −61

La suma de númberos enteros portar de manera similar a la suma de númberos naturales:

La suma de númberos enteros cumple les siguientes propiedaes:

Propiedá asociativa. Daos trés númberos enteros $a$ , $b$ y $c$ , les sumes $(a + b) + c$ y $a + (b + c)$ son iguales.

Propiedá conmutativa. Daos dos númberos enteros $a$ y $b$ , les sumes $a + b$ y $b + a$ son iguales.

Elementu neutru. Tolos númberos enteros $a$ queden inalteraos al suma-yos 0: $a + 0 = a$ .

Exemplu.

Propiedá asociativa:
[ (−13) + (+25) ] + (+32) = (+12) + (+32) = (+44)

(−13) + [ (+25) + (+32) ] = (−13) + (+57) = (+44)
Propiedá conmutativa:
(+9) + (−17) = −8

(−17) + (+9) = −8

Amás, la suma de númberos enteros tien una propiedá adicional que nun tienen los númberos naturales:

Elementu opuestu o simétricu. Pa cada númberu enteru $a$ , esiste otru enteru $- a$ , que sumáu al primeru resulta en cero: $a + (- a) = 0$ .

Resta

La resta de númberos enteros ye bien senciella, yá que agora ye un casu particular de la suma.

La resta de dos númberos enteros (minuendu menos sustraendo) realízase sumando'l minuendu más el sustraendo camudáu de signu.

Exemplos
(+10) − (−5) = (+10) + (+5) = +15
(−7) − (+6) = (−7) + (−6) = −13
(−4) − (−8) = (−4) + (+8) = + 4
(+2) − (+9) = (+2) + (−9) = −7

Multiplicación

La multiplicación de númberos enteros, al igual que la suma, rique determinar por separáu'l signu y valor absolutu de la resultancia.

Na multiplicación (o división) de dos númberos enteros determinar el valor absolutu y el signu de la resultancia de la siguiente manera:

El valor absolutu ye'l productu de los valores absolutos de los factores.

El signu ye «+» si los signos de los factores son iguales, y «−» si son distintos.

Pa recordar el signu de la resultancia, tamién s'utiliza la regla de los signos:

Regla de los signos

(+) × (+)=(+) Más por más igual a más.

(+) × (−)=(−) Más por menos igual a menos.

(−) × (+)=(−) Menos por más igual a menos.

(−) × (−)=(+) Menos por menos igual a más.

Exemplos. (+4) × (−6) = −24 , (+5) × (+3) = +15 , (−7) × (+8) = −56 , (−9) × (−2) = +18.

La multiplicación de númberos enteros tien tamién propiedaes similares a la de númberos naturales:

La multiplicación de númberos enteros cumple les siguientes propiedaes:

Propiedá asociativa. Daos trés númberos enteros $a$ , $b$ y $c$ , los productos $(a \times b) \times c$ y $a \times (b \times c)$ son iguales.

Propiedá conmutativa. Daos dos númberos enteros $a$ y $b$ , los productos $a \times b$ y $b \times a$ son iguales.

Elementu neutru. Tolos númberos enteros $a$ queden inalteraos al multiplicalos por 1: $a \times 1 = a$ .

Exemplu.

Propiedá asociativa:

[ (−7) × (+4) ] × (+5) = (−28) × (+5) = −140

(−7) × [ (+4) × (+5) ] = (−7) × (+20) = −140
Propiedá conmutativa:
(−6) × (+9) = −54

(+9) × (−6) = −54

La suma y multiplicación de númberos enteros tán rellacionaes, al igual que los númberos naturales, pola propiedá distributiva:

Propiedá distributiva. Daos trés númberos enteros $a$ , $b$ y $c$ , el productu $a \times (b + c)$ y la suma de productos $(a \times b) + (a \times c)$ son idénticos.

Exemplu.

(−7) × [ (−2) + (+5) ] = (−7) × (+3) = −21
[ (−7) × (−2) ] + [ (−7) × (+5) ] = (+14) + (−35) = −21

Propiedaes alxebraiques

El conxuntu de los númberos enteros, consideráu xuntu operación adición ye grupu abeliano.

m, n en Z → a+b en Z
m,n, p en z → (m+n)+p = m+(n+p) asociative
cualquier m de Z, con 0, m+0 = 0, cero elementu neutru.
para cualquier m de Z tien -m, m +(-m) = 0. elementu opuestu
Además m+n = n+m

El conxuntu de los númberos enteros, consideráu xunto colos sos operaciones d'adición y multiplicación, tien una estructura qu'en matemátiques se denomina aniellu; y tien una rellación d'orde. Los númberos enteros pueden amás construyise a partir de los númberos naturales por aciu clases d'equivalencia.

Ver tamién

Parte entera
Enteru (tipu de datu)

Referencies

↑ Arias Cabezas, José María; Maza Sáez, Ildefonso (2008). «Aritmética y Álxebra», Matemátiques 1. Madrid: Grupu Editorial Bruño, Sociedá Llindada, páx. 14. ISBN 9788421659854.

Bibliografía

Bayley, R.; Day, R.; Frey, P.; Howard, A.; Hutchens, D. (2006). Mathematics. Applications and Concepts. Course 2 (n'inglés). McGraw-Hill, páx. 21119. ISBN 0-07-865263-4.

Enllaces esternos

Wikcionariu tien definiciones y otra información tocante a númberu enteru.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[ne-1] Arias Cabezas, José María; Maza Sáez, Ildefonso (2008). «Aritmética y Álxebra», Matemátiques 1. Madrid: Grupu Editorial Bruño, Sociedá Llindada, páx. 14. ISBN 9788421659854.

[1]