Cuerpu de los númberos complexos

Los númberos complexos formen un cuerpu, el cuerpu complexu, representáu por C (o más apropiadamente pol caráuter unicode ℂ ). Si identificamos el númberu real a col complexu (a, 0), el cuerpu de los númberos reales R apaez como un subcuerpu de C. Entá más, C forma un espaciu vectorial de dimensión 2 sobre los reales. Los complexos nun pueden ser ordenaos como, por casu, los númberos reales, polo que C nun puede convertise de nenguna manera nun cuerpu ordenáu.

Unidá imaxinaria

Defínese un númberu complexu especial, sobremanera na álxebra, de suma relevancia, el númberu i ( j en física), llamáu unidá imaxinaria, definíu como : ${\displaystyle \mathrm {i} =(0,1)\,\!}$

Que satisfai la siguiente igualdá:

${\displaystyle \mathrm {i} ^{2}=\mathrm {i} \cdot \mathrm {i} =(0,1)\cdot (0,1)=(-1,0)=-1}$

D'onde resulta:

${\displaystyle {\sqrt {-1}}=\mathrm {i} }$

Tomando en cuenta que ${\displaystyle (a,0)\cdot (0,1)=(0,a)}$, cabo la identificación

${\displaystyle (a,0)\cdot (0,1)=a\mathrm {i} =(0,a)}$

Valor absolutu o módulu d'un númberu complexu

La fórmula d'Euler ilustrada nel planu complexu.

El valor absolutu, módulu o magnitú d'un númberu complexu z vien dau pola siguiente espresión:

${\displaystyle |z|={\sqrt {zz^{*}}}={\sqrt {{\hbox{Re}}^{2}(z)+{\hbox{Im}}^{2}(z)}}}$

Si pensamos nes coordenaes cartesianes del númberu complexu z como dalgún puntu nel planu; podemos ver, pol teorema de Pitágoras, que'l valor absolutu d'un númberu complexu coincide cola distancia euclidea dende l'orixe del planu a dichu puntu.

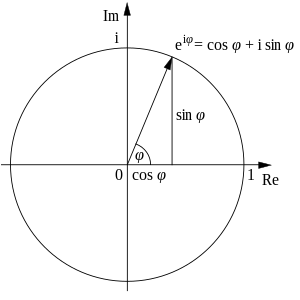
Si'l complexu ta escritu en forma esponencial z = r y^iφ, entós |z| = r. Puede espresase en forma trigonométrica como z = r (cosφ + isenφ), onde cosφ + isenφ = y^iφ ye la conocida fórmula d'Euler.

Podemos comprobar con facilidá estos cuatro importantes propiedaes del valor absolutu

${\displaystyle \left|z\right|=0\Longleftrightarrow z=0}$

${\displaystyle \left|z+w\right|\leq |z|+|w|}$

${\displaystyle \left|zw\right|=|z||w|}$

${\displaystyle \left|z-w\right|\geq |z|-|w|}$

pa cualquier complexu z y w.

Por definición, la función distancia queda como sigue d(z, w) = |z - w| y nos apurre un espaciu métricu colos complexos gracies al que puede falase de llendes y continuidá. La suma, la resta, la multiplicación y la división de complexos son operaciones continues. Si nun se diz lo contrario, asúmese qu'ésta ye la métrica usada nos númberos complexos.

Argumentu o fase

El argumentu principal o fase d'un númberu complexu xenéricu ${\displaystyle z=x+yi\,}$ (siendo x=Re(z) y y=Im(z)) vien dau pola siguiente espresión:

${\displaystyle \phi =\operatorname {Arg} (z)=\operatorname {arreyen2} (y,x)}$

onde arreyen2(y,x) ye la función arcutanxente definida pa los cuatro cuadrantes:

${\displaystyle \operatorname {arreyen2} (y,x)={\begin{cases}\arctan \left({\frac {y}{x}}\right)&\qquad x>0\\\arctan \left({\frac {y}{x}}\right)+\pi &\qquad y\geq 0,x<0\\\arctan \left({\frac {y}{x}}\right)-\pi &\qquad y<0,x<0\\+{\frac {\pi }{2}}&\qquad y>0,x=0\\-{\frac {\pi }{2}}&\qquad y<0,x=0\\{\text{indefiníu}}&\qquad y=0,x=0\end{cases}}}$

O tamién: ${\displaystyle \operatorname {arreyen2} (y,x)={\frac {\pi }{2}}\operatorname {sgn}(y)-\arctan \left({\frac {x}{y}}\right)\quad \forall x,y\in \mathbb {R} }$ Siendo:

${\displaystyle \operatorname {sgn}(y)={\begin{cases}1\qquad y\geq 0\\-1\qquad y<0\\\end{cases}}}$^[3]

la función signu.

L'argumentu tien periodicidá 2π, colo que ${\displaystyle \arg z=\operatorname {Arg} z+2k\pi }$ siendo ${\displaystyle k}$ cualquier númberu enteru. L'ángulu Arg z ye'l valor principal de arg z que verifica les condiciones -π < Arg z <= π descrites antes.^[4]

Conxugáu d'un númberu complexu

Dos binomios llámense conxugaos si solo difieren nel so signu central, por casu, los dos binomios: 3m - 1 y 3m + 1 son conxugaos.

El conxugáu d'un complexu z (denotado como ${\displaystyle {\bar {z}}}$ ó ${\displaystyle z^{*}\,\!}$) ye un nuevu númberu complexu, definíu asina:

${\displaystyle {\bar {z}}=a-\mathrm {i} b\Longleftrightarrow z=a+\mathrm {i} b}$

Reparar que dambos difieren nel signu de la parte imaxinaria.

Con esti númberu cumplen les propiedaes:

${\displaystyle {\overline {z+w}}={\bar {z}}+{\bar {w}}}$

${\displaystyle z+{\overline {z}}=2\cdot {\hbox{Re}}(z)}$

${\displaystyle z-{\overline {z}}=2i\cdot {\hbox{Im}}(z)}$

${\displaystyle {\overline {zw}}={\bar {z}}{\bar {w}}}$

${\displaystyle z\in \mathbb {R} \Longleftrightarrow {\bar {z}}=z}$

${\displaystyle |z|^{2}=z{\bar {z}}}$

${\displaystyle z\neq 0\Rightarrow {\frac {1}{z}}={\frac {\bar {z}}{|z|^{2}}}}$

Esta última fórmula ye'l métodu escoyíu pa calcular l'inversu d'un númberu complexu si vien dau en coordenaes rectangulares.

Un númberu complexu ye igual al so conxugáu si solu si ye un númberu real.

Representación binómica

Un númberu complexu representáu como un puntu (en colloráu) y un vector de posición (azul) nun diagrama de Argand; ${\displaystyle a+bi}$ ye la espresión binomial del puntu.

Un númberu complexu representar en forma binomial como:

${\displaystyle z=a+bi\,}$

La parte real del númberu complexu y la parte imaxinaria, pueden espresase de delles maneres, como s'amuesa de siguío:

${\displaystyle a={\hbox{Re}}(z)=\Re (z)}$

${\displaystyle b={\hbox{Im}}(z)=\Im (z)}$

Representación polar

L'argumentu φ y módulu r alcuentren un puntu nuna diagrama de Argand; ${\displaystyle r(\cos \phi +i\sin \phi )}$ o ${\displaystyle ry^{i\phi }}$ ye la espresión polar del puntu.

Nesta representación, ${\displaystyle \textstyle {r}}$ ye'l módulu del númberu complexu y l'ángulu ${\displaystyle \textstyle {\phi }}$ ye'l argumentu del númberu complexu.

${\displaystyle \textstyle {\phi }=\arctan \left({\frac {b}{a}}\right)=\arctan \left({\frac {{\hbox{Im}}(z)}{{\hbox{Re}}(z)}}\right)=-\arctan \left(-{\frac {{\hbox{Im}}(z)}{{\hbox{Re}}(z)}}\right)}$

${\displaystyle \cos \phi ={\frac {a}{r}}\ ,\ \sin \phi ={\frac {b}{r}}}$

Estenamos a y b nes espresiones anteriores y, utilizando la representación binomial:

${\displaystyle z=a+\mathrm {i} b;\;z=r\cos {\phi }+\mathrm {i} r\sin {\phi }}$

Sacamos factor común r:

${\displaystyle z=r\left(\cos {\phi }+\mathrm {i} \sin {\phi }\right)}$

Frecuentemente, esta espresión embrívese convenientemente de la siguiente manera:

${\displaystyle \ z=r\;\operatorname {cis} \;{\phi }}$

la cual solo contién les abreviatures de les razones trigonométriques cosenu, la unidá imaxinaria y la razón senu del argumentu respeutivamente.

Según esta espresión, puede reparase que pa definir un númberu complexu tantu d'esta forma como cola representación binomial ríquense dos parámetros, que pueden ser parte real ya imaxinaria o bien módulu y argumentu, respeutivamente.

Según la Fórmula d'Euler, vemos que:

${\displaystyle \cos {\phi }+\mathrm {i} \sin {\phi }=y^{\mathrm {i} \phi };\;z=ry^{i\phi }}$

Sicasí, l'ángulu ${\displaystyle \phi }$ nun ta unívocamente determináu por z, pueden esistir infinitos númberos complexos que tienen el mesmu valor representáu nel planu, que s'estremen pol númberu de revoluciones, yá seyan de sentíu antihorario (positives) o horariu (negatives) les cualos represéntense por númberos enteros ${\displaystyle k\in \mathbb {Z} }$, como implica la fórmula d'Euler:

${\displaystyle \forall {k}{\in }\mathbb {Z} \;z=y^{\mathrm {i} (\phi +2\pi {}k)}}$

Por esto, xeneralmente acutamos ${\displaystyle \phi }$ al intervalu [-π, π) y a ésti ${\displaystyle \phi }$ acutáu llamar argumentu principal de z y escribimos φ=Arg(z). Con esti conveniu, les coordenaes taríen unívocamente determinaes por z.

Operaciones en forma polar

La multiplicación de númberos complexos ye especialmente senciella cola notación polar:

${\displaystyle z_{1}z_{2}=rse^{\mathrm {i} (\phi +\psi )}\Leftrightarrow z_{1}z_{2}=ry^{\mathrm {i} \phi }sy^{\mathrm {i} \psi }}$

División:

${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {r}{s}}y^{\mathrm {i} (\phi -\psi )}}$

Potenciación:

${\displaystyle z^{n}=r^{n}y^{\mathrm {i} \phi n}\Leftrightarrow z^{n}=\left(ry^{i\phi }\right)^{n}}$

${\displaystyle z^{n}=(a+b\mathrm {i} )^{n}={n \choose 0}a^{n}+{n \choose 1}a^{n-1}b\mathrm {i} +{n \choose 2}a^{n-2}\left(b\mathrm {i} \right)^{2}+\ldots +{n \choose {n-1}}a\left(b\mathrm {i} \right)^{n-1}+{n \choose n}\left(b\mathrm {i} \right)^{n}}$

En matemátiques

En física

Los númberos complexos usar n'inxeniería electrónica y n'otros campos pa una descripción fayadiza de les señales periódiques variables (ver Analís de Fourier). Nuna espresión del tipu ${\displaystyle z=ry^{i\phi }\,}$ podemos pensar en ${\displaystyle r\,}$ como l'amplitú y en ${\displaystyle \phi \,}$ como la fase d'una onda sinusoidal d'una frecuencia dada. Cuando representamos una corriente o un voltaxe de corriente alterna (y por tanto con comportamientu sinusoidal) como la parte real d'una función de variable complexa de la forma ${\displaystyle f(t)=zy^{i\omega t}\,}$ onde ω representa la frecuencia angular y el númberu complexu z danos la fase y l'amplitú, el tratamientu de toles fórmules que rixen les resistencies, capacidaes y inductores pueden ser unificaes introduciendo resistencies imaxinaries pa los dos últimes (ver redes llétriques). Inxenieros llétricos y físicos usen la lletra j pa la unidá imaxinaria en cuenta de i que ta típicamente destinada a la intensidá de corriente.

El campu complexo ye igualmente importante en mecánica cuántica que la so matemática subxacente utiliza Espacios de Hilbert de dimensión infinita sobre C (ℂ).

Na relatividá especial y la relatividá xeneral, delles fórmules pa la métrica del espaciu-tiempu son muncho más simples si tomamos el tiempu como una variable imaxinaria.

Bibliografía

• Conway, John B., Functions of One Complex Variable I, Springer, ISBN 0-387-90328-3 

Enllaces esternos

• Wikimedia Commons acueye conteníu multimedia sobre Númberu complexu.
• Weisstein, Eric W. «Complex Number» (inglés). MathWorld. Wolfram Research.