Momentu angular d'una masa puntual

El momentu angular d'una partícula con respectu al puntu ${\displaystyle \scriptstyle {O}}$ye'l productu vectorial del so momentu llinial ${\displaystyle \scriptstyle {m\mathbf {v} }}$ pol vector ${\displaystyle \scriptstyle {\mathbf {r} }}$.

En mecánica newtoniana, el momentu angular d'una partícula o masa puntual con al respeutive de un puntu O del espaciu defínese como'l momentu del so cantidá de movimientu ${\displaystyle \mathbf {p} }$ con al respeutive de esi puntu. De normal desígnase por aciu el símbolu ${\displaystyle \mathbf {L} }$. Siendo ${\displaystyle \mathbf {r} }$ el vector que xune'l puntu O cola posición de la masa puntual, va ser

${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {r} \times m\mathbf {v} }$

El vector ${\displaystyle \mathbf {L} \,}$ ye perpendicular al planu que contién ${\displaystyle \mathbf {r} \,}$ y ${\displaystyle \mathbf {v} \,}$, na direición indicada pola regla del productu vectorial o regla de la mano derecha y el so módulu o intensidá ye:

${\displaystyle L=mrv\sin \theta =p\,r\sin \theta =p\,b_{p}}$

esto ye, el productu del módulu del momentu llinial pol so brazu (${\displaystyle b_{p}\,}$ nel dibuxu), definíu ésti como la distancia del puntu respeuto al que se toma'l momentu a la recta que contién la velocidá de la partícula.

Momentu angular y momentu dinámicu

Derivemos el momentu angular con respectu al tiempu:

${\displaystyle {d\mathbf {L} \over dt}={d\ \over dt}(\mathbf {r} \times \mathbf {p} )=\left({d\mathbf {r} \over dt}\times \mathbf {p} \right)+\left(\mathbf {r} \times {d\mathbf {p} \over dt}\right)}$

El primeru de los paréntesis ye cero una y bones la derivada de ${\displaystyle \mathbf {r} \,}$ con respectu al tiempu nun ye otra cosa que la velocidá ${\displaystyle \mathbf {v} \,}$ y, como'l vector velocidá ye paralelu al vector cantidá de movimientu ${\displaystyle \mathbf {p} \,}$, el productu vectorial ye cero. En cuanto al segundu paréntesis, tenemos:

${\displaystyle {d\mathbf {L} \over dt}=\mathbf {r} \times {d\mathbf {p} \over dt}=\mathbf {r} \times {d \over dt}\left(m\mathbf {v} \right)=\mathbf {r} \times (m\mathbf {a} )}$

onde ${\displaystyle \scriptstyle {\mathbf {a} }}$ ye l'aceleración de la partícula, de cuenta que ${\displaystyle m\mathbf {a} =\mathbf {F} \,}$, ye la fuercia qu'actúa sobre ella. Yá que el productu vectorial de ${\displaystyle \mathbf {r} \,}$ pola fuercia ye'l momento o momento dinámicu aplicáu a la masa, tenemos:

${\displaystyle {d\mathbf {L} \over dt}=\mathbf {r} \times \mathbf {F} =\mathbf {M} }$

Asina, la derivada temporal del momentu angular ye igual al momento dinámicu qu'actúa sobre la partícula. Hai que destacar que nesta espresión dambos momentos, ${\displaystyle \mathbf {L} \,}$ y ${\displaystyle \mathbf {M} \,}$ tendrán de tar referíos al mesmu puntu O.

Momentu angular d'un conxuntu de partícules puntuales

El momentu angular d'un conxuntu de partícules ye la suma de los momentos angulares de caúna:

${\displaystyle \mathbf {L} =\sum _{k}{\vec {r}}_{k}\times {\vec {p}}_{k}=\sum \mathbf {L} _{i}\,}$

La variación temporal ye:

${\displaystyle {d\mathbf {L} \over dt}=\sum {d\mathbf {L} _{i} \over dt}=\sum \mathbf {M} _{i}\,}$

El términu de derecha ye la suma de tolos momentos producíos por toles fuercies qu'actúen sobre les partícules. Una parte d'eses fuercies puede ser d'orixe esternu al conxuntu de partícules. Otra parte puede ser fuercies ente partícules. Pero cada fuercia ente partícules tien la so reaición que ye igual pero de direición opuesta y colineal. Eso quier dicir que los momentos producíos por caúna de les fuercies d'un par aición-reaición son iguales y de signu contrariu y que la so suma anúlase. Esto ye, la suma de tolos momentos d'orixe internu ye cero y nun puede faer camudar el valor del momentu angular del conxuntu. Solo queden los momentos esternos:

${\displaystyle {d\mathbf {L} \over dt}=\sum {d\mathbf {L} _{i} \over dt}=\mathbf {M} _{ext.}\,}$

El momentu angular d'un sistema de partícules caltener n'ausencia de momentos esternos. Esta afirmación ye válida pa cualquier conxuntu de partícules: dende nucleos atómicos hasta grupos de galaxes.

Momentu angular d'un sólidu ríxidu

Tenemos que nun sistema inercial la ecuación de movimientu ye:

${\displaystyle {\frac {d\mathbf {L} }{dt}}={\frac {d}{dt}}\left[\mathbf {I} (t)\mathbf {\omega } (t)\right]}$

Onde:

• ${\displaystyle \scriptstyle {\mathbf {\omega } }}$ ye la velocidá angular del sólidu.
• ${\displaystyle \scriptstyle {\mathbf {I} }}$ ye'l tensor d'inercia del cuerpu.

Agora bien, de normal pa un sólidu ríxidu'l tensor d'inercia ${\displaystyle \mathbf {I} }$, depende del tiempu y por tanto nel sistema inercial xeneralmente nun esiste un análogu de la segunda llei de Newton, y nun siendo que el cuerpu xire alredor d'unu de los exes principales d'inercia asocede que:

${\displaystyle {d\mathbf {L} \over dt}\neq \mathbf {I} {d\mathbf {\omega } \over dt}=\mathbf {I} \mathbf {\alpha } }$

Onde ${\displaystyle \scriptstyle {\mathbf {\alpha } }}$ ye l'aceleración angular del cuerpu. Por eso resulta más útil plantegar les ecuaciones de movimientu nun sistema non inercial formáu peles exes principales d'inercia del sólidu, asina se llogra que ${\displaystyle \mathbf {I} ={\mbox{cte.}}}$, anque entós ye necesariu cuntar coles fuercies d'inercia:

${\displaystyle {d\mathbf {L} \over dt}=\mathbf {I} {d\mathbf {\omega } \over dt}+\mathbf {\omega } \times (\mathbf {I} \mathbf {\omega } )}$

Que resulta ser una ecuación non llinial na velocidá angular.

Caltenimientu del momentu angular clásicu

Cuando la suma de los momentos esternos ye cero ${\displaystyle \scriptstyle {\mathbf {M} =0}}$, vimos que:

${\displaystyle {d\mathbf {L} \over dt}=0\,}$

Eso quier dicir que ${\displaystyle \scriptstyle {\mathbf {L} =\mathrm {constante} }}$. Y como ${\displaystyle \scriptstyle {\mathbf {L} }}$ ye un vector, ye constante tantu en módulu como en direición.

Consideremos un oxetu que puede camudar de forma. Nuna d'eses formes, la so Momentu d'inercia ye ${\displaystyle \scriptstyle {I_{1}}}$ y la so velocidá angular ${\displaystyle \scriptstyle {\mathbf {\omega } _{1}}}$. Si l'oxetu camuda de forma (ensin intervención d'un momentu esternu) y que la nueva distribución de mases fai que'l so nuevu Momentu d'inercia sía ${\displaystyle \scriptstyle {I_{2}}}$, la so velocidá angular va camudar de manera tal que:

${\displaystyle \mathbf {I} _{1}\mathbf {\omega } _{1}=\mathbf {I} _{2}\mathbf {\omega } _{2}\,}$

En dellos casos el momentu d'inercia puede considerase un esguilar. Entós la direición del vector velocidá angular nun va camudar. Solo va camudar la velocidá de rotación.

Hai munchos fenómenos nos cualos el caltenimientu del momentu angular tien muncha importancia. Por casu:

• En toles artes y los deportes nos cualos fáense vueltes, reblincaes, etc. Por casu, pa faer una reblincada, una baillarina o una patinadora tomen impulsu colos brazos y una pierna estendida p'aumentar los sos momentos d'inercia alredor de la vertical. Dempués, cerrando los brazos y la pierna, mengüen los sos momentos d'inercia, lo cual aumenta la velocidá de rotación. Pa terminar la reblincada, la estensión de los brazos y una pierna, dexa menguar la velocidá de rotación. Asocede lo mesmo col saltu de plataforma o'l trampolín. Tamién ye importante nel ciclismu y motociclismu, una y bones el caltenimientu del momentu angular ye la responsable de la cencellez con que ye posible caltener l'equilibriu.
• Pa controlar la orientación angular d'un satélite o sonda espacial. Como puede considerase que los momentos esternos son cero, el momentu angular y depués, la orientación del satélite nun camuden. Pa camudar esta orientación, un motor llétricu fai xirar un volante d'inercia. Pa caltener el momentu angular, el satélite poner a xirar nel sentíu opuestu. Una vegada na bona orientación, basta parar el volante d'inercia, lo cual pal satélite. Tamién s'utiliza'l volante d'inercia pa parar les pequeñes rotaciones provocaes polos pequeñu momentos inevitables, como'l producíu pol vientu solar.
• Delles estrelles contráense convirtiéndose en púlsar (estrella de neutrones). El so diámetru mengua hasta unos quilómetros, el so momentu d'inercia mengua y la so velocidá de rotación aumenta descomanadamente. Detectáronse pulsiares con periodo rotación de tan solo unos milisegundos.
• Por cuenta de les marees, la Lluna exerz un momentu sobre la Tierra. Este mengua'l momentu angular de la Tierra y, por cuenta del caltenimientu del momentu angular, el de la Lluna aumenta. Arriendes d'ello, la Lluna aumenta la so enerxía alloñar de la Tierra y menguando la so velocidá de rotación (pero aumentando'l so momentu angular). La Lluna allóñase y los díes y los meses llunares allárguense.

Exemplu

La masa xira tenida por un filo que puede esmucir al traviés d'un tubito delgáu. Tirando del filo camuda'l radiu de xiru ensin modificar el momentu angular.

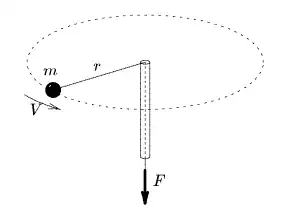
Nel dibuxu de la derecha tenemos una masa que xira, tenida por un filo de masa despreciable que pasa por un tubito finu. Suponemos el conxuntu ensin esfregadures y nun tenemos en cuenta la gravedá.

La fuercia que'l filo exerz sobre la masa ye radial y nun puede exercer un momentu sobre la masa. Si tiramos del filo, el radiu de xiru va menguar. Como, n'ausencia de momentos esternos, el momentu angular caltiénse, la velocidá de rotación de la masa tien d'aumentar.

Un tirón sobre'l filo comunica una velocidá radial ${\displaystyle \scriptstyle {\Delta V}}$ a la masa. La nueva velocidá ye la suma vectorial de la velocidá precedente y ${\displaystyle \scriptstyle {\Delta V}}$

Nel dibuxu siguiente apaez la masa que xira con un radiu ${\displaystyle \scriptstyle {R_{1}}}$ nel momentu nel cual dase un tirón del filo. El términu correutu del "tirón" física ye un impulsu, ye dicir una fuercia aplicao mientres un intre de tiempu. Esi impulsu comunica una velocidá radial ${\displaystyle \scriptstyle {\Delta V}}$ a la masa. La nueva velocidá va ser la suma vectorial de la velocidá precedente ${\displaystyle \scriptstyle {V}}$ con ${\displaystyle \scriptstyle {\Delta V}}$. La direición d'esa nueva velocidá nun ye tanxencial, sinón entrante. Cuando la masa pasa pol puntu más próximu del centru, a una distancia ${\displaystyle \scriptstyle {R_{2}}}$, cobramos el filo sueltu y la masa va siguir a xirar col nuevu radiu ${\displaystyle \scriptstyle {R_{2}}}$. Nel dibuxu, el triángulu mariellu y el triángulu rosado son asemeyaos. Lo cual déxanos escribir:

${\displaystyle {V_{2} \over V_{1}}={R_{1} \over R_{2}}\,}$

esto ye:

${\displaystyle V_{1}R_{1}=V_{2}R_{2}\,}$

Y, si multiplicamos pola masa ${\displaystyle \scriptstyle {m}}$, llogramos que'l momentu angular caltúvose, como lo esperábamos:

${\displaystyle mV_{1}R_{1}=mV_{2}R_{2}\,}$

Vemos como'l momentu angular caltúvose: P'amenorgar el radiu de xiru hai que comunicar una velocidá radial, que aumenta la velocidá total de la masa.

Tamién puede faese l'esperimentu nel otru sentíu. Si suelta'l filo, la masa sigue la tanxente de la trayeutoria y el so momentu angular nun camuda. A un ciertu momentu frenamos el filo por que'l radiu sía constante de nuevu. El fechu de frenar el filo, comunica una velocidá radial (escontra'l centru) a la masa. Esta vegada esta velocidá radial mengua la velocidá total y solo queda la componente de la velocidá tanxencial al filo na posición na cual frenar.

Nun ye necesariu faer la esperiencia dando un tirón. Puede faese de manera continua, una y bones la fuercia que se fai reponiendo y soltando filo puede descomponese nuna socesión de pequeños impulsos.

Momentu angular orbital

El momentu angular orbital, tal como'l que tien un sistema de dos partícules que xira una alredor de la otra, puede tresformase a un operador ${\displaystyle {\hat {L}}}$ por aciu la so espresión clásica:

${\displaystyle \mathbf {\hat {L}} =-i\hbar \left(\mathbf {r} \times {\boldsymbol {\nabla }}\right)}$

siendo ${\displaystyle \mathbf {r} }$ la distancia que les dixebra.

Usando coordenaes cartesianes los trés componentes del momentu angular espresar nel espaciu de Hilbert avezáu pa les funciones d'onda, ${\displaystyle L^{2}(\mathbb {R} ^{3})}$, como:

${\displaystyle {\hat {L}}_{x}=-i\hbar \left(y{\frac {\partial }{\partial z}}-z{\frac {\partial }{\partial y}}\right)\qquad {\hat {L}}_{y}=-i\hbar \left(z{\frac {\partial }{\partial x}}-x{\frac {\partial }{\partial z}}\right)\qquad {\hat {L}}_{z}=-i\hbar \left(x{\frac {\partial }{\partial y}}-y{\frac {\partial }{\partial x}}\right)}$

Sicasí en coordenaes angulares esfériques el cuadráu del momentu angular y la componente Z esprésense como:

${\displaystyle \ {\hat {L}}^{2}=-\hbar ^{2}\left[{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}\right]\qquad {\hat {L}}_{z}=-i\hbar \left({\frac {\partial }{\partial \varphi }}\right)}$

Los vectores propios o estaos propios del momentu angular orbital dependen de dos númberos cuánticos enteros ${\displaystyle l}$ y ${\displaystyle m}$, desígnense como ${\displaystyle |l,m\rangle }$ y satisfaen les rellaciones:

${\displaystyle {\hat {L}}^{2}|l,m\rangle ={\hbar }^{2}l(l+1)|l,m\rangle \qquad {\hat {L}}_{z}|l,m\rangle =\hbar m|l,m\rangle }$

Estos vectores propios espresaos en términos de les coordenaes angulares esfériques son los llamaos harmónicos esféricos Y_{l, m}(θ,φ), que se constrúin a partir de los polinomios de Legendre:

${\displaystyle \langle \theta ,\phi |l,m\rangle =Y_{l,m}(\theta ,\varphi )\qquad Y_{l,m}(\theta ,\varphi )=N\,y^{im\varphi }\,P_{l}^{m}(\cos {\theta })}$

Tienen especial importancia por ser la componente angular de los orbitales atómicos.

Caltenimientu del momentu angular cuánticu

Ye importante notar que si'l hamiltoniano nun depende de les variables angulares, como asocede por casu en problemes con potencial de simetría esférica entós toles componentes del momentu angular conmutan col hamiltoniano:

${\displaystyle \left[{\hat {L}}_{i},H\right]=0}$

y, de resultes, el cuadráu del momentu angular tamién conmuta col Hamiltoniano:

${\displaystyle \left[{\hat {L}}^{2},H\right]=0}$.

Y tenemos que'l momento angular caltiénse, eso significa qu'a lo llargo de la evolución nel tiempu del sistema cuánticu la distribución de probabilidá de los valores del momentu angular nun va variar. Nótese sicasí que como les componentes del momentu angular non conmutan ente sigo non pueden definise simultáneamente. Sicasí, si pueden definise simultáneamente el cuadráu del momentu angular y una de los sos componentes (davezu escuéyese la componente Z). En particular si tenemos estaos cuánticos pel momento bien definíu estos van siguir siendo estaos cuánticos pel momento bien definíu colos mesmos valores de los númberos cuánticos ${\displaystyle l}$ y ${\displaystyle m}$.