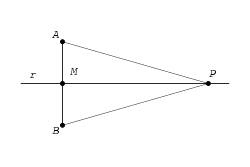

La mediatriz d'un segmentu ye'l llugar xeométricu de los puntos del planu qu'equidisten de los estremos del segmentu. Esti llugar xeométricu, ye la reuta perpendicular al segmentu pol so puntu mediu.
La mediatriz dixebra un segmentu en dos partes iguales, y el so ángulu ye reutu.
La llinia que cumple toes estes condiciones nún ángulu, nómase bisectriz.
Aplicación
Nún triángulu ABC, les mediatrices de los tres llaos córtense nún puntu únicu, el circuncentru ( na figura) que ye'l centru de la circunferencia circunscrita al triángulu.
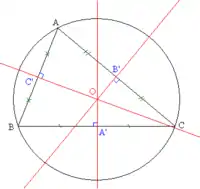
Si trazamos la mediatriz del llau , sabemos que cualquier puntu allugáu nesa mediatriz equidista tanto de A como de B.
Si facemos agora la mediatriz de , cualquier puntu allugáu nesta otra mediatriz, cumplirá qu'equidista de B y C. Estes dos mediatrices, córtense en O, puntu común y equidistante de los puntos (vértices) A, B y C. El puntu O ye'l Circuncentru del triángulu.
Si se fai la mediatriz del llau pasará de xuru por O.
El puntu O ye'l puntu equidistante de los tres vértices, poro, ye'l centru d'una circunferencia que pasa polos tres puntos. Esta circunferencia ye la circunferencia circunscrita al triángulu.