Modelu matemáticu

Nel modelu plantegáu pola mecánica de medios continuos les magnitúes físiques como la enerxía o la cantidá de movimientu pueden ser remanaes na llende infinitesimal. Por esa razón les rellaciones básiques en mecánica de medios continuos tomen la forma d'ecuaciones diferenciales. Los tipos básicos d'ecuaciones usaes en mecánica de medios continuos son:

• Ecuaciones constitutives que caractericen les propiedaes del material que trata de modelase como mediu continuu.
• Ley de caltenimientu que son lleis física fundamentales como:
  • Caltenimientu de la enerxía.
  • Caltenimientu de la cantidá de movimientu

Yá que les propiedaes de los sólidos y fluyíos nun dependen del sistema de coordenaes escoyíu pal so estudiu, les ecuaciones de la mecánica de medios continuos tienen forma tensorial. Esto ye, les magnitúes básiques qu'apaecen na mecánica de medios continuos son tensores lo cual dexa escribir les ecuaciones nuna forma básica que non varia d'un sistema de coordenaes a otru.

Movimientu del mediu

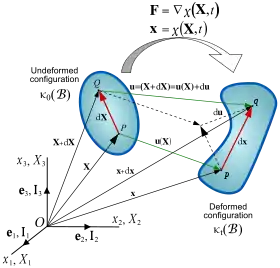
El movimientu de mediu continuu precisa especificar cómo se mueve cada unu de los puntos materiales que componen el mediu a lo llargo del tiempu. Eso implica que nun basta un númberu finito de coordenaes sinón pa cada puntu ríquese una función del tiempu que describa la so posición en cada intre. Usualmente la descripción del movimientu realizar a partir d'una configuración inicial. Esta configuración inicial ta formada por tolos puntos del espaciu que primeramente taben ocupaos pel mediu continuu, polo que'l movimientu puede realizase por aciu una aplicación del tipu:

${\displaystyle {\begin{cases}{\boldsymbol {\varphi }}:\Omega _{0}\times \mathbb {R} \to \mathbb {R} ^{3}\\(\mathbf {X} ,t)\mapsto \mathbf {x} \end{cases}}}$

El movimientu del puntu material de coordenaes iniciales ${\displaystyle \scriptstyle \mathbf {X} }$ va venir dau por:

${\displaystyle \mathbf {x} ={\boldsymbol {\varphi }}_{t}(\mathbf {X} )={\boldsymbol {\varphi }}(\mathbf {X} ,t)}$

A partir d'esa función puede definise el gradiente de deformación en cada puntu como la derivada jacobiana de l'anterior aplicación:

${\displaystyle \mathbf {F} _{t}:=D{\boldsymbol {\varphi }}_{t},\qquad F_{ij,t}={\frac {\partial \varphi _{i,t}}{\partial X^{j}}}}$

A partir d'esi gradiente puede definise'l tensor deformación y el tensor velocidá de deformación. Y a partir d'ellos en función del tipu de material que forme'l mediu continuu puede llograse el tensor de tensiones por aciu la ecuación constitutiva del mediu.

Sólidos y fluyíos

La diferencia fundamental ente sólidos deformables y fluyíos ye que les tensiones nun puntu nun intre dau nos sólidos vense influyíes pol valor actual de la deformación ${\displaystyle {\boldsymbol {\varepsilon }}}$ en dichu puntu, esto ye, les tensiones dependen de cuanto difier la "forma orixinal" o configuración natural y l'estáu actual. Otra manera, nun fluyíu les tensiones nun puntu namái dependen d'un esguilar llamáu presión (p) y de la velocidá de deformación ${\displaystyle {\boldsymbol {\dot {\varepsilon }}}}$, pero non la deformación mesma. Por casu nun sólidu elásticu homoxéneu ecuación constitutiva tien la forma:

${\displaystyle {\boldsymbol {\sigma }}(\mathbf {x} ,t)=T({\boldsymbol {\varepsilon }}(\mathbf {x} ,t))}$

Ente que un fluyíu tien una ecuación constitutiva d'un fluyíu ye del tipu:

${\displaystyle {\boldsymbol {\sigma }}(\mathbf {x} ,t)=T({\boldsymbol {\dot {\varepsilon }}}(\mathbf {x} ,t),p)=-p\mathbf {I} +{\hat {T}}({\boldsymbol {\dot {\varepsilon }}}(\mathbf {x} ,t))}$

Un sólidu viscoelástico tien tensiones que siguen dependiendo de la deformación anque al igual qu'un fluyíu'l valor de la tensión vese afeutáu pola velocidá de deformación, asina un sólidu viscoelástico homoxéneu de tipu diferencial podría tener una ecuación constitutiva del tipu:

${\displaystyle {\boldsymbol {\sigma }}(\mathbf {x} ,t)=T({\boldsymbol {\varepsilon }}(\mathbf {x} ,t),{\boldsymbol {\dot {\varepsilon }}}(\mathbf {x} ,t))}$

Ye interesante notar que la ecuación d'equilibriu:

${\displaystyle \rho {\frac {D\mathbf {v} }{Dt}}=\nabla \cdot {\boldsymbol {\sigma }}+\rho \mathbf {f} }$

Onde

${\displaystyle \rho \ }$ ye la densidá del mediu.

${\displaystyle \scriptstyle {\frac {D}{Dt}}}$ ye la derivada material, :${\displaystyle \mathbf {v} }$

ye'l campu de velocidaes, :${\displaystyle \rho \mathbf {f} }$ ye la densidá de fuercia por unidá de masa :${\displaystyle {\boldsymbol {\sigma }}}$ ye'l tensor tensión Ye válida tantu pa sólidos deformables como para fluyíos. Nel casu de fluyíos newtonianos se substituye el tensor tensión pola espresión constitutiva en términos de la velocidá de deformación la ecuación anterior convertir na ecuación de Navier-Stokes pal fluyíu.

Bibliografía

• Eringen, A. Cemel (1980). Mechanics of Continua, 2nd edition, Krieger Pub Co. ISBN 0-88275-663-X.
• Dimitrienko, Yuriy (2011). Nonlinear Continuum Mechanics and Large Inelastic Deformations. Alemaña: Springer. ISBN 978-94-007-0033-8.
• Fung, Y. C. (1977). A First Course in Continuum Mechanics, 2nd edition, Prentice-Hall, Inc.. ISBN 0-13-318311-4.
• Gurtin, M. Y. (1981). An Introduction to Continuum Mechanics. Nueva York: Academic Press.
• Maugin, G. A. (1999). The Thermomechanics of Nonlinear Irreversible Behaviors: An Introduction. Singapore: World Scientific.